绪论
10-15章节我们介绍了数据结构中重要的一部分——树的概念和一些较为重要的应用。从Lecture 16,我们开始介绍数据结构重要的另外一个部分——图。
事实上,从图论的角度来看,树应该是隶属于图这部分知识的一个重要部分,树是特殊的一类图。但从很多功能的实现来看,由于树有根节点到各个结点的路径唯一和无环的性质,同样的功能在树结构实现起来可以看作图结构的简化,我个人觉得这是在介绍图的问题之前先介绍树的原因。
16-1主要还是介绍图的基本概念·······介绍了好几遍了。
Undirected Graphs
首先需要知道图这种数据结构描述了些什么样的概念?从离散数学的术语来说,图描述了若干个元素组成的集合和元素与元素之间的二元组(二元关系两个元素之间的相对次序是有意义的)组成的集合,简单来说,就是一个数据结构包括了若干个同类型的元素以及他们两两之间的关系。
图与只存储元素的简单数据结构的差别就在于元素与元素之间存在的联系需要作为一个对象进行存储。
例如从组词听起来和图数据结构最相关的对象——图片(这里以最简单的存储方式为例),由n*m的像素点组成,每个像素点有色号等信息,相邻的像素点存在上下左右的关系,但我们其实可以发现这些关系对整个图片或者像素点的信息几乎没有任何的影响,所以不需要进行存储,只需要简单的二阶数组数据结构即可。
但对于同样的n*m方阵,我们现在希望从某个方格到某个方格,点可以根据规则从某个点到另外的点,对于这个问题,这个规则下定义出来的某个点到某个点的“指向”是我们需要进行操作和关注的对象。此时的方阵就可以构成一个图的数据结构,“指向”就是存在于元素与元素之间的关系。
元素在图中称为顶点,二元组称为边,我们可以根据二元组构成的连通关系是否为偏序关系将图分为有向图和无向图,即有向图边存在明确的点到点的方向,无向图边的两个点不存在一个点到另一个点的方向,从哪个点到哪个点都可以。
我个人还是建议先打好离散数学的基础再来学习数据结构中的图,这样会有很多不一样的认识,因为图论实际上本来就是组合数学重要的一部分,计算机类的书籍对图论部分的介绍和解释很多都是断续的,强行理解记忆起来会存在很多的障碍和困惑。
这里我们只对课本上提到的概念进行介绍,首先是无向图:
Vertices
顶点集合我们用大V表示:

Edges
边就是点与点之间的关系,无向图边的两个点不存在相对关系。边的集合用大E表示:

数据结构中研究的图一般为简单图,即无平行边和自环的图,不包含平行边就是指两个点之间最多只能存在一条边,无自环就是指不存在一个点到自己的边,这样我们可以推测出边数量的最大值。

Degree
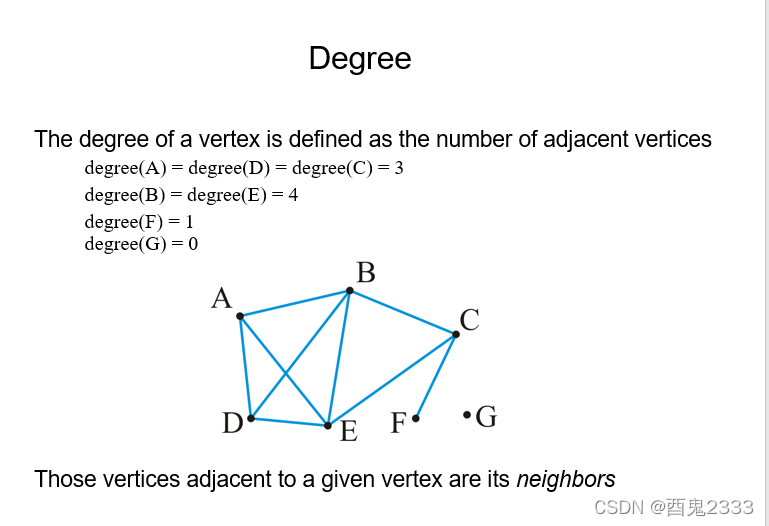
deg就是度,度是顶点的属性,指的是与顶点关联的边的数量,那什么叫做关联呢?如果一个顶点是一条边的两个顶点之一,那么我们称这个点与这条边关联。
所有与某个顶点相邻的顶点称为这个顶点的邻居(neighbors),离散数学中叫邻域。
Sub-graphs
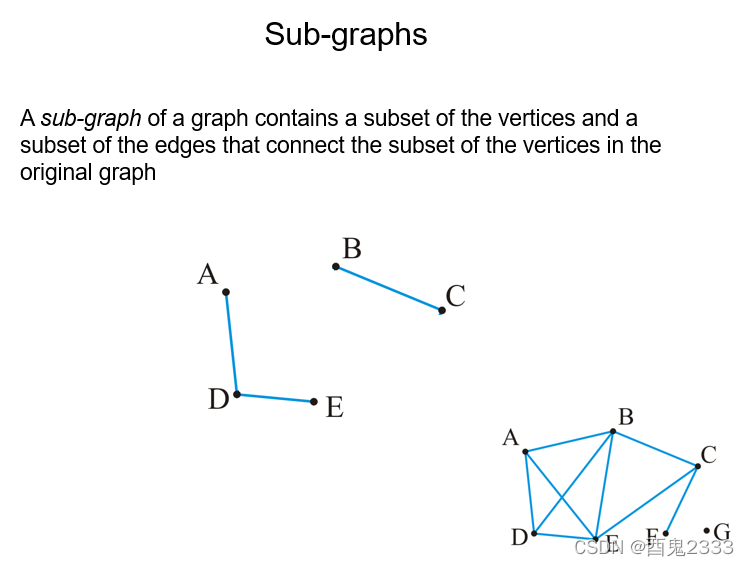
sub前缀是附属和代替的意思,这个附属在数学中更倾向于“子”或者说“被包含”,那么sub-graphs的意思很好理解,就是被包含的图,也就是子图的意思。
子图的顶点集为母图顶点集的子集,边集为母图边集的子集,且不能出现子图边集中出现的顶点在子图的顶点集中不存在的情况,即还需要满足图本身的性质。
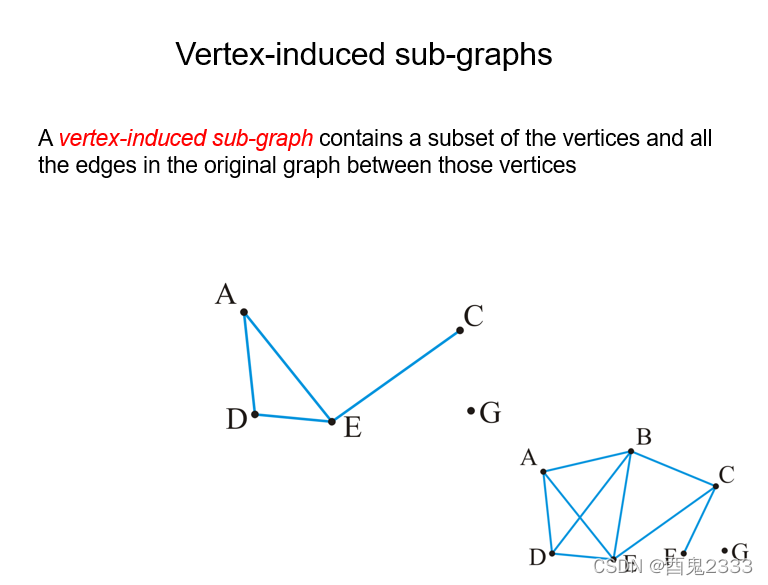
说到子图,就不得不说导出子图。导出子图是子图中的一个特殊情况,要求在母图中存在的边,如果两个点都存在于子图的顶点集中,那么这条边也必须存在于子图的边集中,即导出子图是由母图顶点集的某个子集所能构成的边数最多的最大子图。
由于导出子图只用顶点集就能够确定,英文愿意为“由顶点引导的子图”。
Paths,Connectedness
路径在树中提到过了,这里就不再赘述了,因为解释起来真的很麻烦,课件上的解释也不是很好。
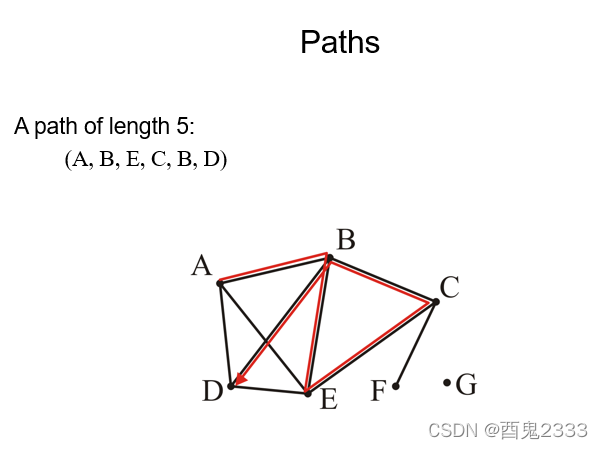
简单来说,从点A到点B的路径,就是以顶点A为第一个元素,顶点B为最后一个元素的顶点序列,其中序列任意的两个相邻元素,即两个顶点之间存在边。

只有一个顶点组成的序列对应的路径长度为0,即自己到自己的路径。
一般路径对应的顶点序列中出现的顶点是可以重复的。
结点没有重复的路径称为简单路径,同理有简单环(simple circle)。
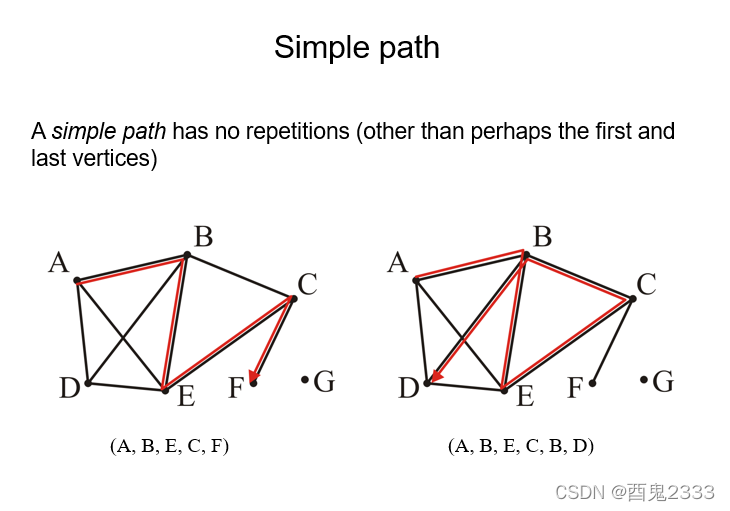
如果两个结点之间存在路径(不说一个点到一个点的,因为是无向图,没有指定的方向),那么称这两个节点是相通的。
Weighted graphs
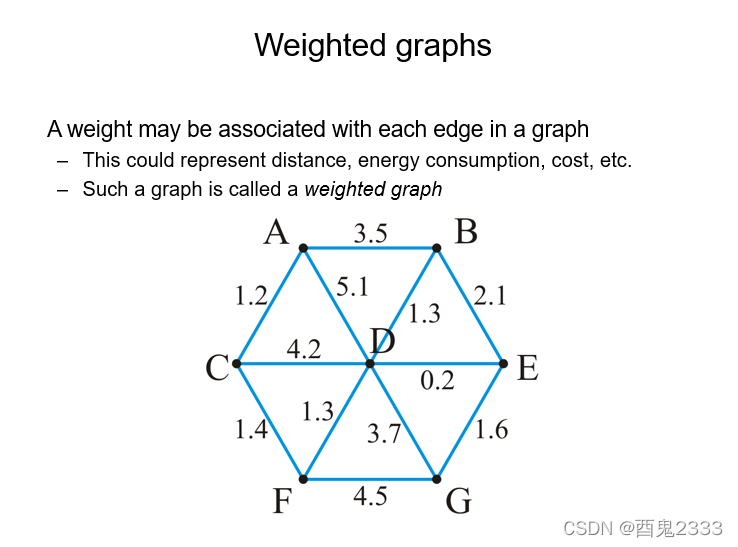
我们知道边在图的是数据结构中是看作一个独立的对象的,如果边作为对象存在数值一类的属性,我们就称这个图为加权图(Weighted graphs)。
这个数值类是我自己这样描述的,实际上这里没有确定的说明,常见的是花费,消耗,距离等。就是说这个数值不是单纯的数字,还是需要能够解释为“份额”,“占比”的对象。
例如我们现在给每条边定义一个属性,这个属性可能为1或-1,表示你通过这条边时会产生两种不一样的变化, 此时虽然每条边上的1和-1都是数值,但是就这个定义不能该图为加权图。
Trees
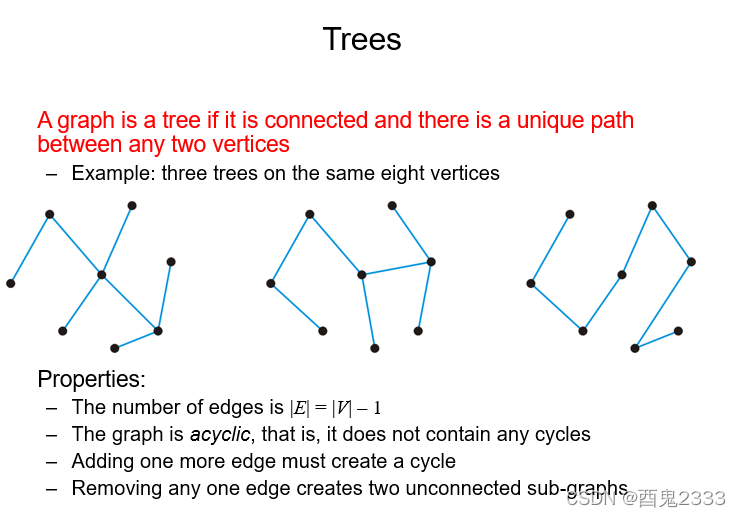
如果一个图中的任意两个结点连通,且存在唯一的路径,我们称这个图为树。
有关树的性质很多,这些性质的不同结合也能给予树不同的定义:
1.树边的个数等于结点的个数-1。
2.树中不存在环。
3.给树添加一条边,一定能够产生一个环,
4.去掉一条边就会使得整个图不再连通
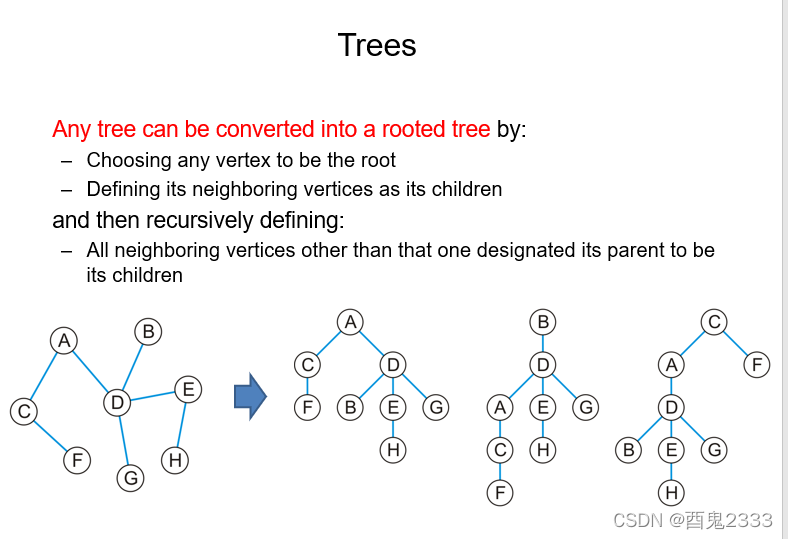
上述的树我们称为无根树,只需要选择任意一个结点作为根,邻居作为子节点就可以得到一颗有根树。
每个连通子图都是树的图就是森林(连通子图等概念就不单独拿出来解释了)。
Directed graphs
有向图就是给无向图的每条边定义了从其中一个顶点到另一个顶点的方向。

In and out degrees
有向图度的定义和无向图其实是一样的,只是因为对于有向图的边,两个顶点分为起点和终点,于是有了某个点被作为起点的次数的出度(out_degrees)和作为终点的次数的入度(in_degrees),出度和入度之和即为度。

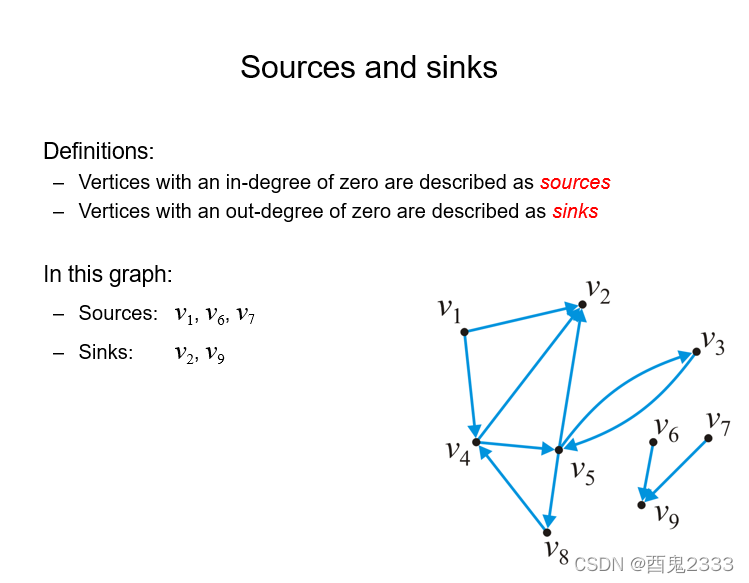
其中只出不入的点称为sources,只入不出的点称为sinks。
Connectedness
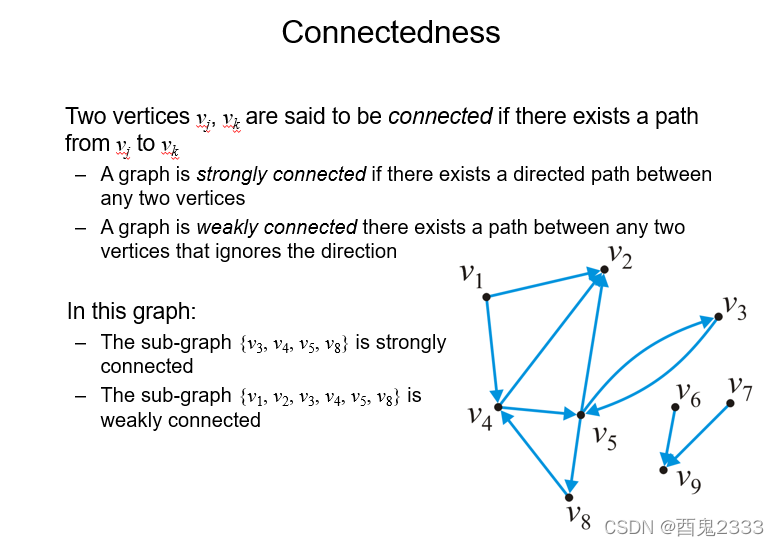
路径上和无向图没什么区别,对于有向图中的两个点A和B,如果同时存在A到B的路径和B到A的路径,那么称他们两个点是强连通的(strongly connected),如果A到B的路径和B到A的路径仅存在一条,那么称两点为弱连通的(weakly connected),无论强连通或弱连通都是连通。
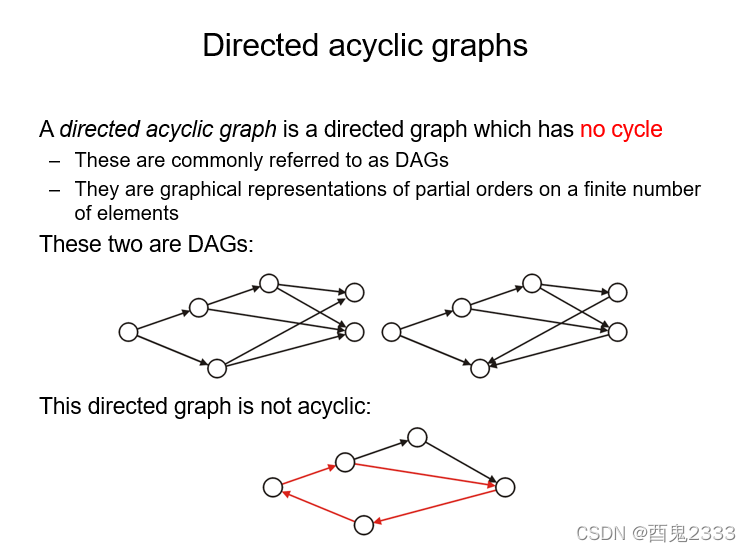
Directed acyclic graphs
就是常说的DAG,字面意思有向而无环的图。
Representation
就是将图的信息存储下来的不同存储结构。
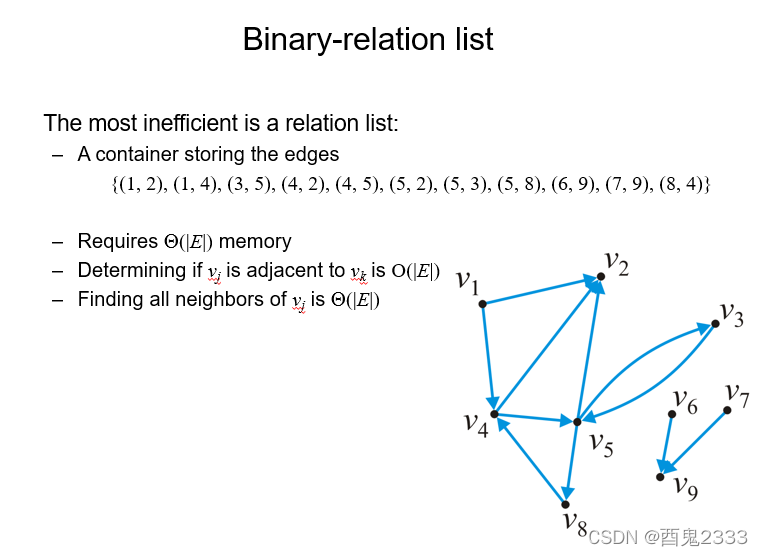
Binary-relation list
翻译了一下,直译是二元关系表,就是将所有的二元组用pairs进行顺序存储,和稀疏矩阵的三元表存储结构类似。
Adjacency matrix
第二种表达方式就是邻接矩阵,矩阵的行和列分别代表某个结点,矩阵第n行第m列的元素代表第n个结点和第m个结点是否存在边或边的权值(对于有权图,课件上有图示,这里就不多赘述了,因为是很简单的东西)。
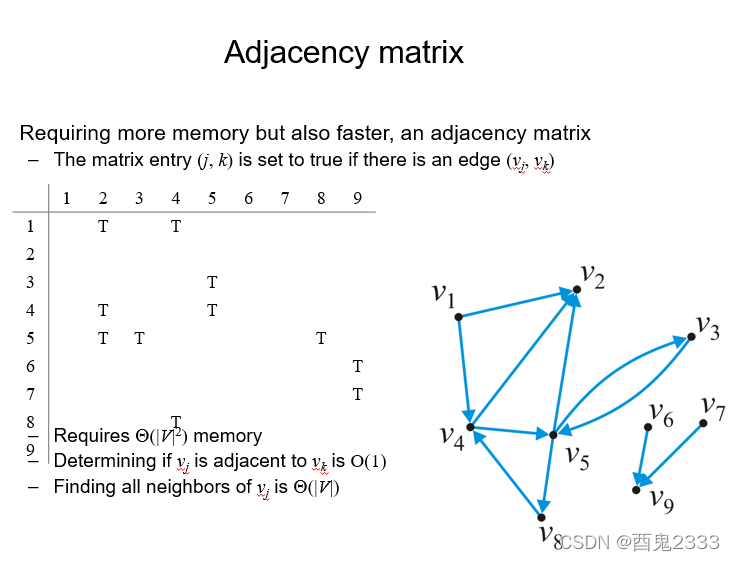
因为需要将所有可能出现的边的情况全部准备在那里,空间开销是很大的,但同时在知道两个结点信息的情况下找到边的效率也是很高的。

对于有权图,初始化将每条边的长度设置成INF(无穷大),因为我们认为不存在边的两个结点无法连通,即两个结点之间的距离是无穷的。同理自己到自己的距离为0(具体怎么初始化向具体情况靠拢,不要有思维定势,不过一般要么是-1要么是INF)。

无权图就是要么连通要么没连通,按照布尔型存储即可。

当矩形中有效值的占比小于等于5%(这个比例是灵活的,根据需要自己设定),我们称这个矩阵为稀疏矩阵,也就是说我们可以用存储稀疏矩阵的方式来存储这个矩阵。
不过事实上存储稀疏矩阵的两种方式——三元表和十字矩阵,三元表类似于二元关系表,十字矩阵在实际使用上往往不如我们后面要介绍的邻接表。
Adjacency list
第三种实现方式据说是最为流行的实现方式,也就是邻接表。邻接表的实现方式是顺序与链式结合,第i行依旧代表与第i个结点相邻的点,只是这些点不像邻接矩阵预先准备结点数量的空间,而是像单链表一样实际有多少相邻的顶点准备多少空间,将这些相邻的顶点用单链表存储起来。

对于无向图,为了减少空间的消耗,例如边(2,3),我们只将它存储在结点2的单链表中,即边编号较小结点的单链表中。

总结
和课本上基本就一样,图论毕竟是一门数学,还是直接看数学相关的书籍比较好。存储方式多了一个二元关系表,不过实际上就是和三元表差不多hhhh。