什么是多元线性回归?
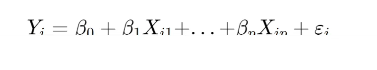
用矩阵来进行表示为:
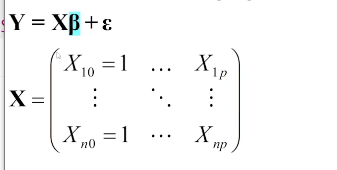
实现

模型的p-value表示我这三个系数要不要的显著性
注:大部分操作与简单线性回归完全相同
把所有变量都用来分析:快捷

可以发现:
Multiple R-squared随着变量数量的增加始终提升,可以解释为变量解释的误差占总误差的比例越来越大。
Adjusted R-squared并不一定,暗示变量不是越多越好。最大的模型中,尽管模型显著,胆没有任何一个变量是显著的。这也是为什么要做模型选择的原因。
修正已有拟合模型
第一个 . 表示要预测的变量y,第二个 . 表示之前的变量。然后加上新的变量。


交叉项
如果感觉现有模型还不够好,可以考虑加入交叉项

对于类别型变量比如就只有0 1这种类别,解释:使得其他变量对不同分组存在不同的影响(系数不同)
共线性
如果有部分向量互相相关,则这两个变量会互相影响导致估计的误差很大,严格相关时,会导致部分变量无法估计。
例如 y = 3x可以写成y = x+2x = 0*x+1.5x就会导致无法估计。

这个可以用来估计共线性,越大就越可能存在越相关。
因此变量越多并不一定越好,容易出现过拟合等问题。
模型选择
这里我们暂时先考虑变量选择,即选出少量重要的因素。
有很多选择方法,没有哪个是绝对最优的。使用以下方法:AIC:



逐步去筛选,删去哪个变量,看看对应的AIC,AIC越小越好。第一步做全部变量的AIC,发现可以把cyl删去,一步步的进行,直到删去某一个值不会发生减少甚至增大为止。
注:AIC含义:参数越少/误差越小,AIC越小(模型越好)
backward选出的并不一定是AIC最小的那个模型,但差不多还可以。
这里是一个前向搜索。选出的答案可能是不一样的。

BIC: step(k = log(n))
AIC和BIC不能确定哪个更好。
模型比较
统计意义上论证某些变量是否可以去除还需要模型比较
一般比较一个full model和一个reduce model
做法就是把减少的那些变量置于0,看看效果

看那个F值比较大,说明去掉几个变量之后的会更好一点。