[数据结构与算法]【2022省选模拟】[ZROI] 赢王——结论、线段树

原题链接会404所以就自己乱挂了一个

题目描述

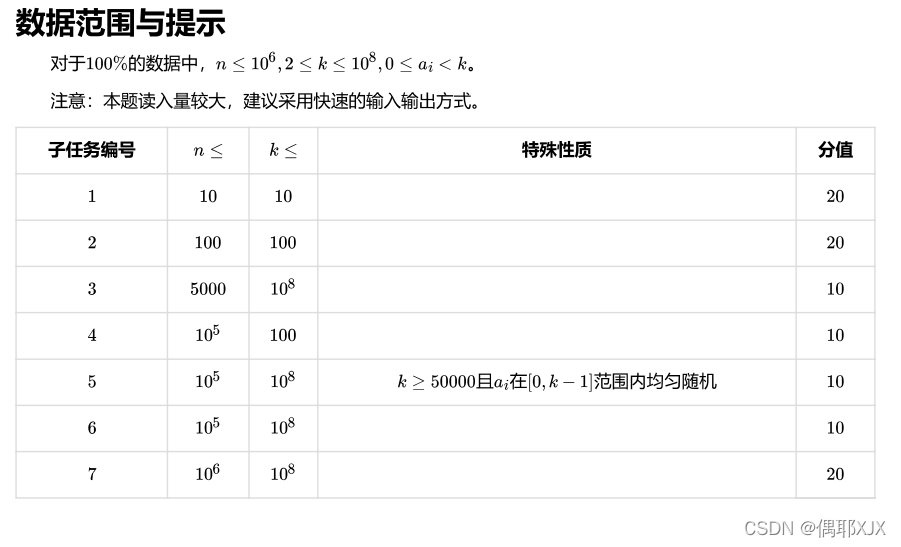
题解

如果我们把数列看成是一条数轴上的 $n?1$ 个隔板：

那么一次操作等价于把一个隔板向左或向右挪一单位，且毫不影响其它的隔板。我们的目的是让所有隔板的位置都为 $k$ 的倍数，所以对于一个有解的合法区间（满足 $a_i$ 的和为 $k$ 的倍数），最优方案一定是每个隔板朝着离它最近的 $k$ 的倍数的位置挪过去：

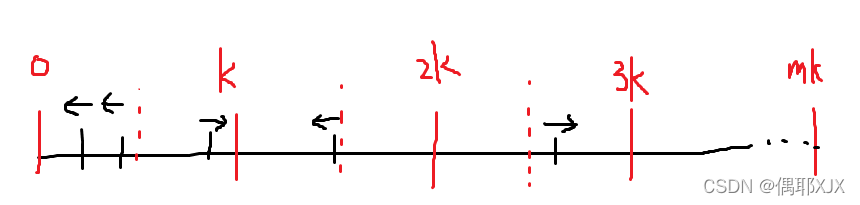
知道了结论过后，我们要怎么统计答案呢？我们可以考虑以每个 $r$ 结尾的区间的 $f$ 的和。通过上边的结论我们知道，如果区间中间存在一个隔板初始就是 $k$ 的倍数位置，那么这个区间可以被分半，答案是前一半和后一半的和。所以我们可以对于每个 $r$ 求出最近的 $l$，使得 $[l,r]$ 是个合法区间，然后在求出所有 $f(a_l...a_r)$ 之后再利用 $l$ 做一个简单DP即可。

每个 $r$ 对应的 $l$ 是很好求的，剩下的问题就是怎么快速求 $f(a_l,a_r)$。

我们考虑一个暴力做法，从一个 $l$ 开始往后扫，依次统计每个隔板的贡献，这样计算完一个区间是 $O(n)$ 的。

考虑加速这个过程，我们对数列进行扫描线，同时对前面的所有 $l$，维护从它们开始往后的区间的贡献和。考虑当前已经维护了 $[0,k)$ 中若干位置的答案，现在加入一个 $a_r$，那么这些位置要同时在 $\mathrm{m}\mathrm{o}\mathrm{d}k$ 意义下往后挪 $a_r$ 作为新的隔板位置，此时对 $[0,\frac{k}{2}]$ 中的位置，贡献会依次加上 $0,1,2,...,\frac{k}{2}$，对 $(\frac{k}{2},k)$ 中的位置，贡献会依次加上 $k?\frac{k}{2}?1,...,2,1$。此时我们只需要维护整体的位移，然后用线段树进行区间覆盖上一个等差数列的操作，维护单点值即可。

剩下就是一些优化了。考虑到线段树的值域大小为 $k$，直接用动态开点很容易MLE，所以要先把关键点离散化再建立普通线段树，这样空间就是 $O(n)$ 的。整体位移一定不要用平衡树，常数太大了，你只需要在外记录一个整体位移的标记即可。考虑到我们做的是区间修改、单点查询，并且这个等差数列的懒标记是可以永久化的，所以用仅维护懒标记的zkw线段树可以大大缩小该做法的常数。

这个做法是 $O(n\log n)$ 的，但其实还有常数更小的主席树或树状数组的做法，这里就不提了。

代码

#include<bits/stdc++.h>//JZM yyds!!
#define ll long long
#define uns unsigned
#define IF (it->first)
#define IS (it->second)
#define END putchar('\n')
using namespace std;
const int MAXN=1000005;
const ll INF=1e18;
inline ll read(){
	ll x=0;bool f=1;char s=getchar();
	while((s<'0'||s>'9')&&s>0){if(s=='-')f^=1;s=getchar();}
	while(s>='0'&&s<='9')x=(x<<1)+(x<<3)+(s^48),s=getchar();
	return f?x:-x;
}
int ptf[50],lpt;
inline void print(ll x,char c='\n'){
	if(x<0)putchar('-'),x=-x;
	ptf[lpt=1]=x%10;
	while(x>9)x/=10,ptf[++lpt]=x%10;
	while(lpt)putchar(ptf[lpt--]^48);
	if(c>0)putchar(c);
}
inline ll lowbit(ll x){return x&-x;}

const ll MOD=998244353;
int n,k,a[MAXN],s[MAXN],b[MAXN],sr[MAXN],m;
int pm[MAXN],pr[MAXN],cnt[MAXN];
ll dp[MAXN];
ll f[MAXN<<2],g[MAXN<<2];
int zl[MAXN<<2],zr[MAXN<<2],p;
inline void init(int n){
	for(p=1;p<n+2;p<<=1);
	for(int i=1;i<=n;i++)zl[p+i]=zr[p+i]=b[i];
	for(int i=(p+n+2)>>1;i;i--)zl[i]=zl[i<<1],zr[i]=zr[i<<1|1];
}
inline ll MID(ll a,ll b,int l,int r,int z){
	if(l==r)return a;
	return a+(b-a)/(r-l)*(z-l);
}
inline void add(int l,int r,ll a,ll b,int c,int d){
	if(l>r)return;
	for(l=p+l-1,r=p+r+1;l^1^r;l>>=1,r>>=1){
		if(~l&1)f[l^1]+=MID(a,b,c,d,zl[l^1]),g[l^1]+=MID(a,b,c,d,zr[l^1]);
		if(r&1)f[r^1]+=MID(a,b,c,d,zl[r^1]),g[r^1]+=MID(a,b,c,d,zr[r^1]);
	}
}
inline ll sch(int x){
	int z=b[x];ll res=0;
	for(x=p+x;x;x>>=1)res+=MID(f[x],g[x],zl[x],zr[x],z);
	return res;
}
inline void doadd(int l,int r,ll c,ll d){
	int bl=lower_bound(b+1,b+1+m,l)-b,br=lower_bound(b+1,b+1+m,r+1)-b-1;
	if(l<=r)add(bl,br,c,d,l,r);
	else{
		add(bl,m,c,MID(c,d,l,r+k,b[m]),l,b[m]);
		add(1,br,MID(c,d,l-k,r,b[1]),d,b[1],r);
	}
}
signed main()
{
	freopen("win.in","r",stdin);
	freopen("win.out","w",stdout);
	n=read(),k=read(),sr[n+1]=k-1;
	for(int i=1;i<=n;i++)
		a[i]=read(),s[i]=(s[i-1]+a[i])%k,sr[i]=s[i],pr[i]=-1;
	sort(sr,sr+n+2),b[m=1]=0;
	for(int i=1;i<=n+1;i++)if(sr[i]^sr[i-1])b[++m]=sr[i];
	init(m);
	for(int i=1;i<=m;i++)pm[i]=-1;
	pm[1]=0;
	for(int i=1;i<=n;i++){
		int x=lower_bound(b+1,b+1+m,s[i])-b;
		dp[i]=sch(x),add(x,x,-dp[i],-dp[i],s[i],s[i]);
		if(pm[x]>=0)pr[i]=pm[x];
		pm[x]=i;
		doadd((s[i]-(k>>1)+k)%k,s[i],k>>1,0);
		doadd(s[i],(s[i]+k-1-(k>>1))%k,0,k-1-(k>>1));
	}
	ll ans=0;
	for(int i=1;i<=n;i++){
		if(pr[i]<0)dp[i]=MOD-i;
		else{
			dp[i]=(dp[i]%MOD+MOD)%MOD,cnt[i]=cnt[pr[i]]+1;
			dp[i]=(dp[i]*cnt[i]%MOD+dp[pr[i]]-i+pr[i]+1+MOD)%MOD;
		}
		ans+=dp[i];
		if(ans>=MOD)ans-=MOD;
	}
	print(ans);
	return 0;
}
/*
5 3
1 2 2 1 1
*/