文章目录
0.前言
hello 大家好,准备新开一个刷题专栏,记录自己刷题经历,刷题时要注重每一题的优化,由于知识受限,现在很多优化都还做不到,不过没关系,等以后学得多了,还会反复刷这些题的。每次的记录也是督促自己。

1.移除元素

给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
暴力循环
查找到每一个val,依次挪动数据,从后往前覆盖
时间复杂度O(N^2),最坏情况,大部分都是val
实际上也跑不过,超时了。

//暴力双循环,只不过时间复杂度不符合
int removeElement(int* nums, int numsSize, int val)
{
int size = numsSize;
for(int i = 0; i<numsSize;i++)
{
if(nums[i] == val)
{
for(int j=i+1;j<size;j++)
{
nums[j-1] = nums[j];
}
i--;//出了if之后,i就会立刻++,防止接连出现val时出现遗漏
size--;
}
}
return size;
}
空间换时间
把不是val的值,拷贝放到新数组里,最后再拷贝回去
时间复杂度O(N),空间复杂度O(N)
不符合要求。
双指针
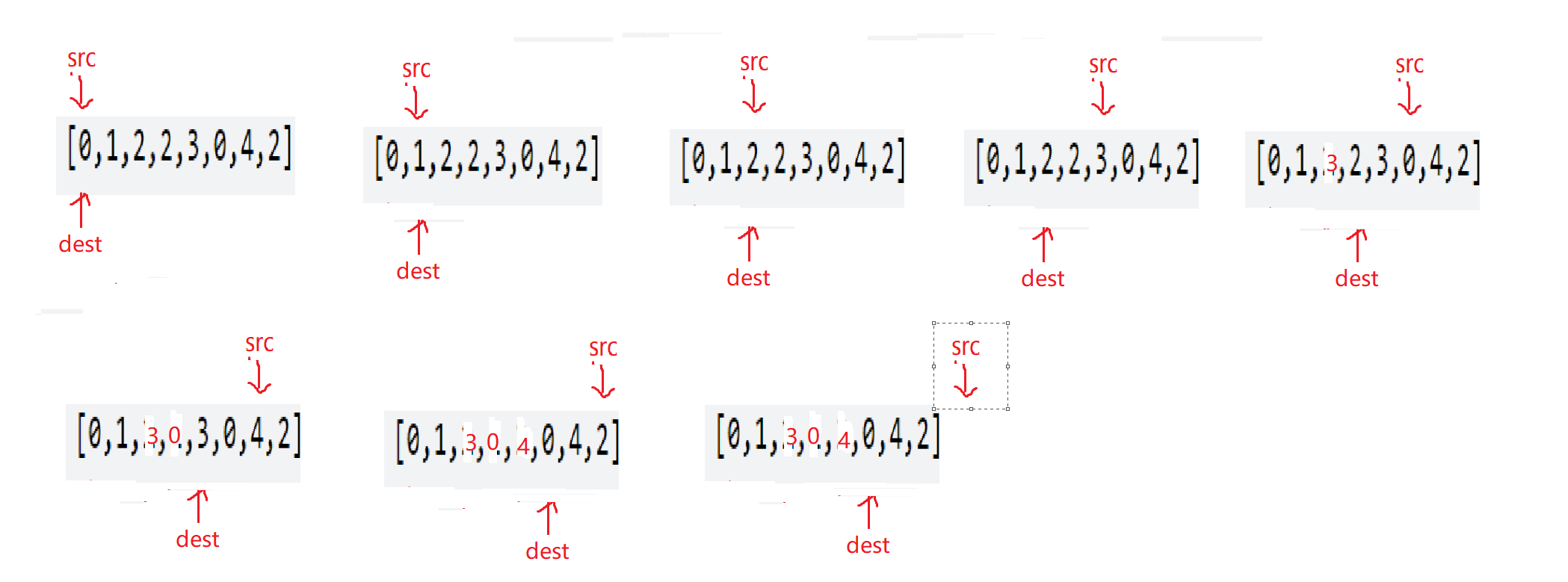
如果右指针指向的元素不等于 val,它一定是输出数组的一个元素,我们就将右指针指向的元素复制到左指针位置,然后将左右指针同时右移;
如果右指针指向的元素等于 val,它不能在输出数组里,此时左指针不动,右指针右移一位。
int removeElement(int* nums, int numsSize, int val)
{
int left = 0;
for(int right = 0; right<numsSize;right++)
{
if(nums[right] != val)
{
nums[left] = nums[right];
left++;
}
}
return left;
}
同一个思路,另一种写法
int removeElement(int* nums, int numsSize, int val)
{
int src = 0;
int dst = 0;
while(src < numsSize)
{
if(nums[src] == val)
++src;
else
nums[dst++] = nums[src++];
}
return dst; //题目要求返回新长度,恰好就是dst的值
}
双指针优化
如果要移除的元素恰好在数组的开头,例如序列 1 2 3 4 5当 val为 1时,我们需要把每一个元素都左移一位。
注意到题目中说:「元素的顺序可以改变」。实际上我们可以直接将最后一个元素 5 移动到序列开头,取代元素 1,得到序列5 2 3 4 5同样满足题目要求。
这个优化在序列中 val 元素的数量较少时非常有效。
class Solution
{
public:
int removeElement(vector<int> &nums, int val)
{
int left = 0, right = nums.size();
while (left < right)
{
if (nums[left] == val)
{
nums[left] = nums[right - 1];
right--;
}
else
{
left++;
}
}
return left;
}
};
2.删除有序数组中的重复项
双指针1
slow fast从0开始 s 1 2 2 3 4 4 f s 1 2 2 3 4 4 f s 1 2 2 3 4 4 f s 1 2 2 3 4 4 f s 1 2 3 3 4 4 f s 1 2 3 4 4 4 f s 1 2 3 4 4 4 f 结束,slow此时坐标为3,应该返回slow+1 注意要考虑数组为空的情况
第一种写法,自己写的有点挫。其实应该一开始就把 slow 和 fast 分离的。
int removeDuplicates(int* nums, int numsSize)
{
//快慢指针
if(numsSize == 0)
return 0;
int slow = 0, fast = 0;
while(fast < numsSize)
{
if(nums[slow] == nums[fast])
fast++;
else
{
slow++;
nums[slow] = nums[fast];
fast++;
}
}
return slow+1;//slow一开始为0
}
双指针2
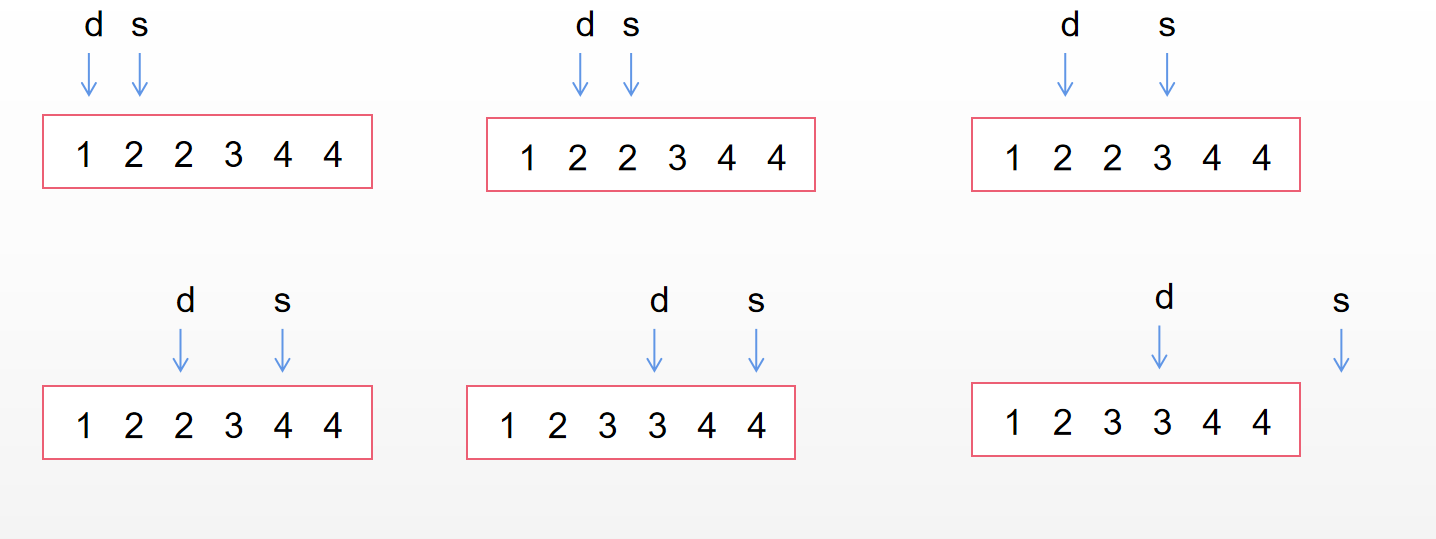
核心就是一段区间一段区间的去处理,
nums[src] 跟 nums[src - 1] 值不相等时,说明前一段重复区间已经走完。
由于src走到最后就越界,不能再去 src-1 比较,因此需要把最后一个值拷给dst。
每次nums1[dst] 被重新赋值后,就要dst++,这样最终返回的dst恰好就是去重后的元素个数。
时间复杂度O(N)
int removeDuplicates(int* nums, int numsSize)
{
int src = 1, dst = 0;
while(src < numsSize)
{
if(nums[src] == nums[src-1])
src++;
//不相等说明前一段重复区间已经走完
else
{
nums[dst] = nums[src-1];
dst++;
src++;
}
}
//注意需要把最后一个值再拷过来
nums[dst] = nums[numsSize-1];
dst++;
//dst一定要每次放一个值就++一次
return dst;
}
3.合并两个有序数组
memove+qsort
利用好库里的函数 memmove 和 qsort
[[11.字符串+内存函数#memmove | memmove]]
[[10.指针进阶#qsort函数|qsort]]
int CompareByint(const void* e1, const void* e2)
{
return *(int*)e1 - *(int*)e2;
}
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
memmove(nums1+m,nums2,n*sizeof(nums2[0]));
qsort(nums1, m+n, sizeof(nums1[0]), CompareByint);
//nums1Size == m + n
return nums1;
}
双指针:
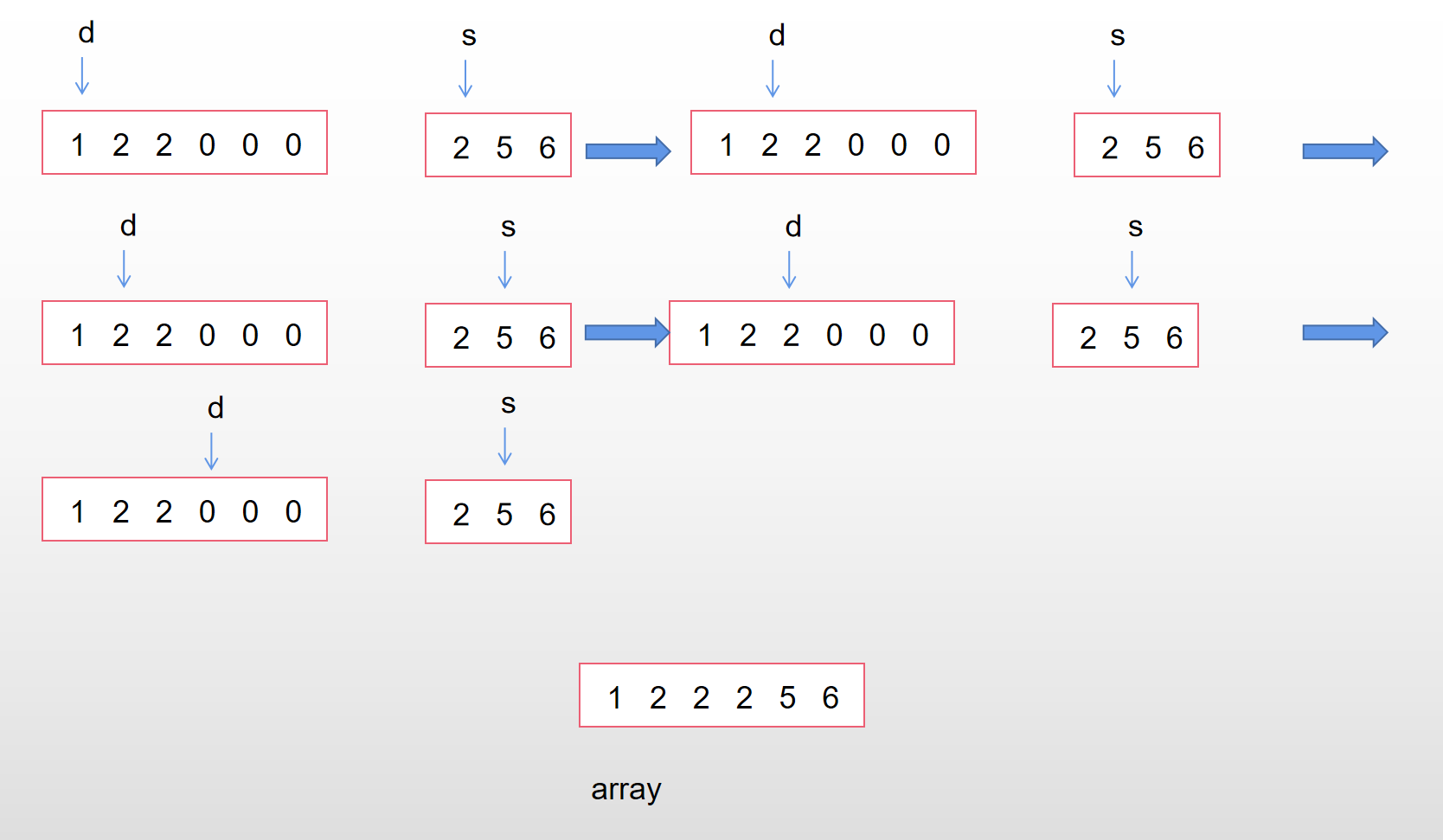
以空间换时间
额外开辟一个数组,把小的放到新的数组里,最后再赋值给nums1
其实就是归并的思路。空间复杂度O(N) 时间复杂度O(N)
注意:题目给的nums1空间大小是m+n,后面的n个位置是空的,就是为了放nums2的元素
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
//双指针,额外开辟一个数组,把小的放到新的数组里,最后再赋值给nums1
int array[m+n];
int dst = 0, src = 0;//dst指向nums1,src指向nums2
for(int i = 0; i < n+m; i++)
{
if(dst == m)
{
array[i] = nums2[src];
src++;
}
else if(src == n)
{
array[i] = nums1[dst];
dst++;
}
else if(nums1[dst] < nums2[src])
{
array[i] = nums1[dst];
dst++;
}
else if(nums1[dst] >= nums2[src])
{
array[i] = nums2[src];
src++;
}
}
//将array的值赋值给nums1
for(int i = 0; i < m+n; i++)
{
nums1[i] = array[i];
}
}
另一种写法:
void merge(int *nums1, int nums1Size, int m, int *nums2, int nums2Size, int n)
{
int p1 = 0;
int p2 = 0;
int sorted[m + n];
while (p1 < m || p2 < n)
{
if (p1 == m)
{
sorted[p1 + p2 - 1] = nums2[p2++];
}
else if (p2 == n)
{
sorted[p1 + p2 - 1] = nums1[p1++];
}
else if (nums1[p1] < nums2[p2])
{
sorted[p1 + p2 - 1] = nums1[p1++];
}
else
{
sorted[p1 + p2 - 1] = nums2[p2++];
}
}
for (int i = 0; i < m + n; i++)
{
nums1[i] = sorted[i];
}
}
//额外开辟数组,空间复杂度是O(N)
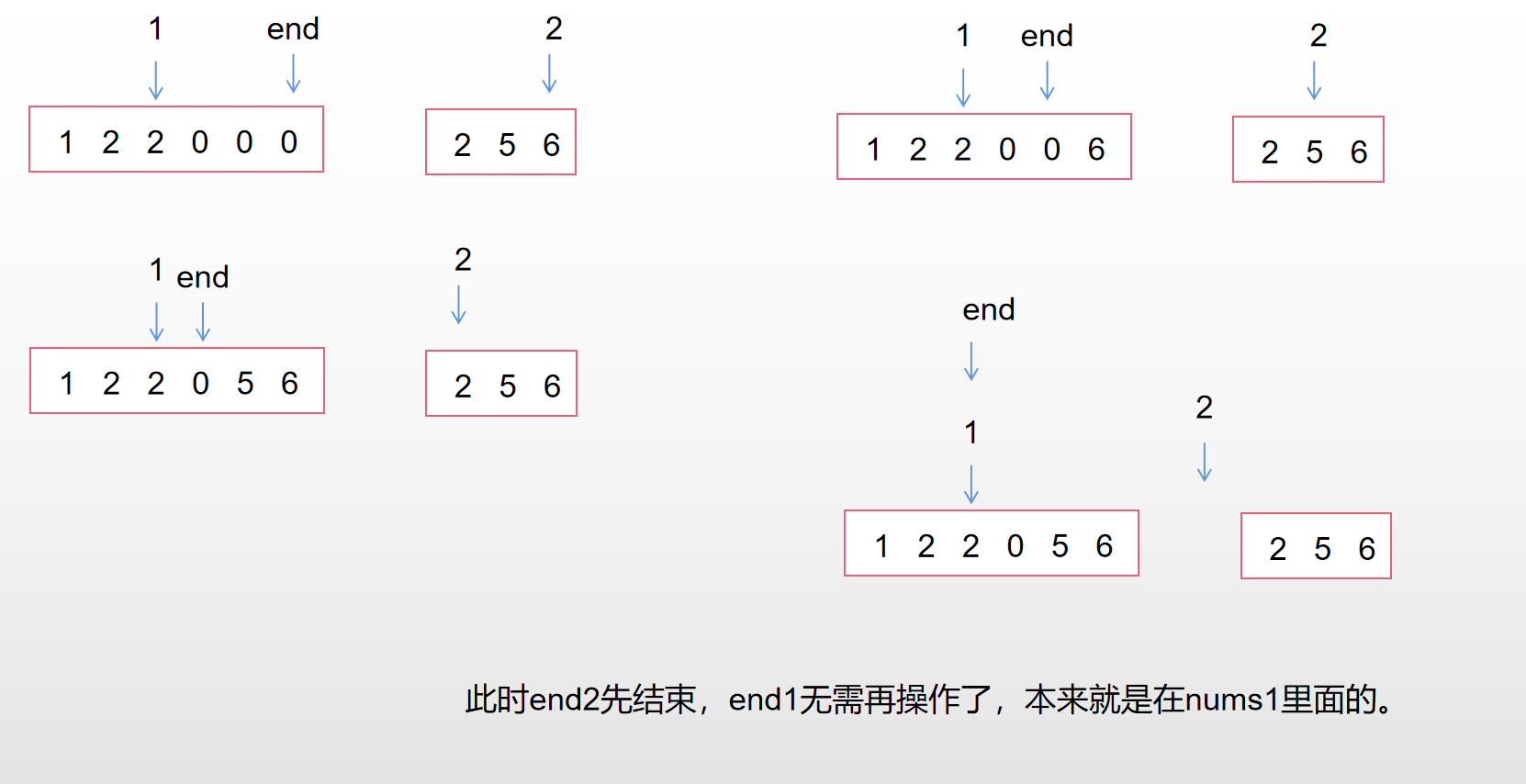
三指针:
比较数据,把大的从后往前放,不需额外开辟数组
空间复杂度O(1)
考虑极端情况,nums2先走完了,或者nums1先走完了
void merge(int *nums1, int nums1Size, int m, int *nums2, int nums2Size, int n)
{
int end1 = m - 1;
int end2 = n - 1;
int end = m + n - 1;
while (end1 >= 0 && end2 >= 0)//有一个结束了就结束了,但我们要写继续走的条件。
{
if (nums1[end1] > nums2[end2])
{
nums1[end--] = nums1[end1--];
}
else
{
nums1[end--] = nums2[end2--];
}
}
// end2结束了,end1还有数据,无需挪动
// end1先结束,需要把end2的数据放到nums1里面
while (end2 >= 0)
{
nums1[end--] = nums2[end2--];
}
}
//时间复杂度O(m+n) 空间复杂度O(1)
另一种写法
void merge(int *nums1, int nums1Size, int m, int *nums2, int nums2Size, int n)
{
int end1 = m - 1;
int end2 = n - 1;
int end = m + n - 1;
while (end1 >= 0 || end2 >= 0)
{
if (-1 == end1)
{ // end1为-1说明nums1里面没有元素
nums1[end--] = nums2[end2--];
}
else if (-1 == end2)
{ // nums2没有元素
nums1[end--] = nums1[end1--];
}
else if (nums1[end1] >= nums2[end2])
{ //谁大谁就放进
nums1[end--] = nums1[end1--];
}
else if (nums1[end1] <= nums2[end2])
{
nums1[end--] = nums2[end2--];
}
}
}
4.轮转数组

思路一:
右旋k次,临时保存最后一个数,依次向右移动一次
时间复杂度O(N*K) 空间复杂度O(1)但是当 k % N = N-1时,时间复杂度 --》O(N^2)
k % N = N 时,也就是不旋转。
void rotate(int *nums, int numsSize, int k)
{
int end = numsSize - 1;
int temp = 0;
for (int i = 0; i < k; i++)
{
temp = nums[end];
for (int j = end; j > 0; j--)
{
nums[j] = nums[j - 1];
}
nums[0] = temp;
}
}
思路二:
以空间换时间
额外开一个空间,把后k个数放到最前面,前N-K个数顺次放到后面[1,2,3,4,5,6,7] k=3
[5,6,7,1,2,3,4]时间复杂度O(N) 空间复杂度O(N)
void rotate(int* nums, int numsSize, int k){
//开辟一个数组,以空间换时间,把后面k个数放到前面,前面n-k个数放到数组后面
int array[numsSize];
k %= numsSize;//避免k过大
for(int i = 0; i < k; i++)
{
array[i] = nums[numsSize-k+i];
}
//前面n-k个数放到数组后面
for(int i = 0; i < numsSize-k; i++)
{
array[k+i] = nums[i];
}
//再把array放到nums里面去
for(int i = 0; i < numsSize; i++)
{
nums[i] = array[i];
}
return nums;
}
//更简洁的写法
void rotate(int* nums, int numsSize, int k)
{
int newArr[numsSize];
for(int i=0; i<numsSize; i++)
{
newArr[(i+k)%numsSize] = nums[i];
}
for(int i=0; i<numsSize; i++)
{
nums[i] = newArr[i];
}
}
思路三:
3次逆置
对原数组后k个数逆置
对原数组前n-k个数逆置
对原数组整体逆置
[1,2,3,4,5,6,7] ,k=3
4 3 2 1 5 6 7
4 3 2 1 7 6 5
5 6 7 1 2 3 4时间复杂度O(N) 空间复杂度O(1)
void Reverse(int* arr, int left, int right)
{
while(left<right)
{
int tmp = arr[right];
arr[right] = arr[left];
arr[left] = tmp;
left++;
right--;
}
}
void rotate(int* nums, int numsSize, int k)
{
k %= numsSize;//避免k过大越界,k=numsSize+1 --> 翻转1次
Reverse(nums, 0, numsSize-k-1);//前N-K个
Reverse(nums, numsSize-k, numsSize-1);//后K个
Reverse(nums, 0, numsSize-1);//整体
}
//想不清楚时,举个样例就好
5.尾声
🌵🌵
写文不易,如果有帮助烦请点个赞~ 👍👍👍
🌹🌹Thanks?(・ω・)ノ🌹🌹
👀👀由于笔者水平有限,在今后的博文中难免会出现错误之处,本人非常希望您如果发现错误,恳请留言批评斧正,希望和大家一起学习,一起进步ヽ( ̄ω ̄( ̄ω ̄〃)ゝ,期待您的留言评论。
[附GitHub仓库链接
