问题说明:
八皇后问题,是一个古老而著名的问题,是回溯算法的典型例题。该问题是十九世纪著名的数学家高斯1850年提出:
在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。高斯认为有76种方案。
1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。在计算机问世后有更多的方法。
问题分析:
对于一个8 x 8的棋盘来说,我们很容易想象到使用二维数组来解决这个问题,但实际上我们只需要使用一个一维数组。
我们通过一维数组arr[8]来解决,首先我们可以利用下标 i 用来代表行数-1,arr[i]中的值代表列数-1,这样我们就很好的完成了对于一个棋盘的设计。
步骤:
1. 将第一个王后放在第一行的第一列。
2. 将第二个皇后放置第二行的第一列,然后进行判断是否满足条件,如果不满足则放置在第二列、第三列...,直到满足条件。
3. 继续第三个皇后放置第三行的第一列,然后继续判断是否满足,如果不满足则放置第二列、第三列... 。
4. 当得到一个正确的解后,我们可以将其打印出来,然后进行回溯,重新回到第一步,然后重复2、3、4步,直到所有的情况都结束,完成程序。
代码实现如下:
public class Queue02{
static int Max=8;
static int a[]=new int[Max];
static int count=0;
public static void main(String[] args){
put(0);
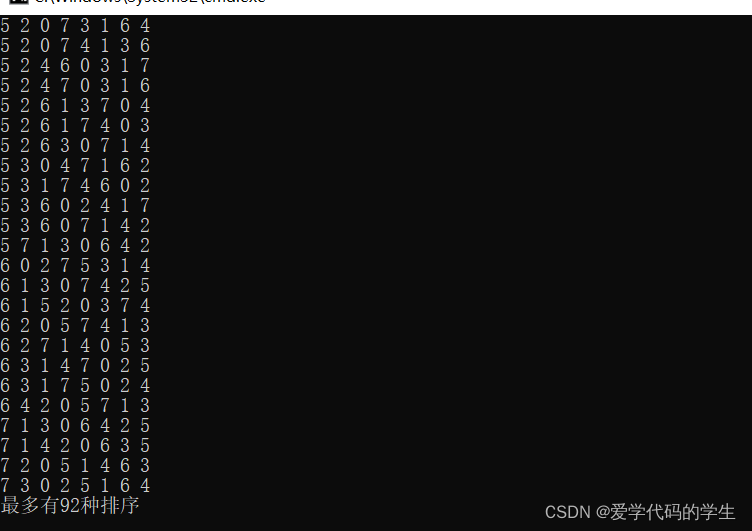
System.out.println("最多有"+count+"种排序");
}
public static void print(){
count++;
for(int i=0;i<Max;i++){
System.out.print(a[i]+" ");
}
System.out.println();
}
public static boolean judge(int n){
for(int i=0;i<n;i++){
if(a[n]==a[i] || n-i==Math.abs(a[n]-a[i])){
return false;
}
}
return true;
}
public static void put(int n){
//打印完结束
if(n == Max){
print();
return;
}
for(int i=0;i<Max;i++){
a[n]=i;
if(judge(n)){
put(n+1);
}
}
}
}
?就此实现八皇后问题。