程序内功篇六--树
一、树
1、树的含义
树(Tree)是n(n≥0)个节点的有限集合T,它满足两个条件 :
有且仅有一个特定的称为根(Root)的节点;- 其余的节点可以分为m(m≥0)个互不相交的有限集合
T1、T2、……、Tm,其中每一个集合又是一棵树,并称为其根的子树
表示方法 :
树形表示法、目录表示法。

2、树的特点(选看)
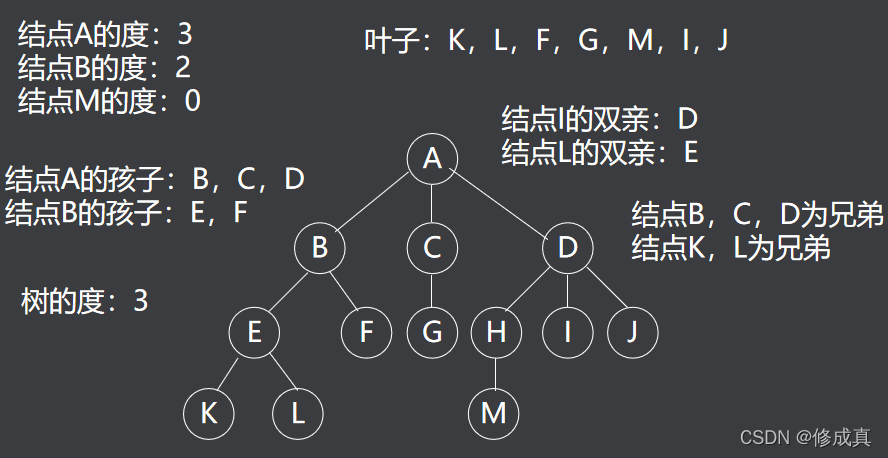
(1)结点与度数
- 一个
节点的子树的个数称为该节点的度数 一棵树的度数是指该树中节点的最大度数度数为零的节点称为树叶或终端节点- 度数
不为零的节点称为分支节点 - 除根节点外的
分支节点称为内部节点。
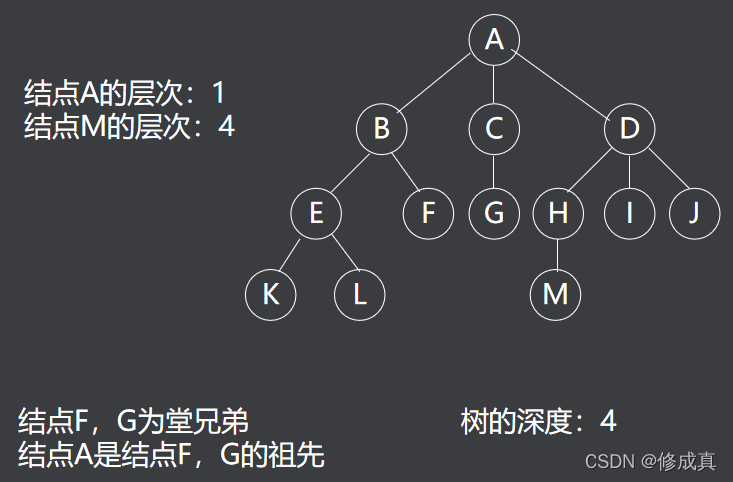
(2)路径与层数
- 一个节点系列k1,k2, ……,ki,ki+1, ……,kj,并满足
ki是ki+1的父节点,就称为一条从k1到kj的路径 - 路径的长度为
j-1,即路径中的边数。 - 路径中前面的节点是后面节点的祖先,后面节点是前面节点的子孙。
节点的层数等于父节点的层数加一,根节点的层数定义为一。树中节点层数的最大值称为该树的高度或深度。
(3)有序树与森林
- 若树中
每个节点的各个子树的排列为从左到右,不能交换,即兄弟之间是有序的,则该树称为有序树。 m(m≥0)棵互不相交的树的集合称为森林。- 树去掉根节点就成为
森林,森林加上一个新的根节点就成为树。
3、树的逻辑结构
树中任何节点都可以有零个或多个直接后继节点(子节点),但至多只有一个直接前趋节点(父节点),
根节点没有前趋节点,叶节点没有后继节点。
二、二叉树
1、二叉树的含义
二叉树是n(n≥0)个节点的有限集合或者是空集(n=0)或者是由一个根节点以及两棵互不相交的.
分别称为左子树和右子树的二叉树组成
严格区分左孩子和右孩子,即使只有一个子节点也要区分左右。
2、二叉树性质
- 二叉树
第i(i≥1)层上的节点最多为2^(i-1)个。 深度为k(k≥1)的二叉树最多有2^k-1个节点。
满二叉树 :深度为
k(k≥1)时有2k-1个节点的二叉树。
完全二叉树 :只有
最下面两层有度数小于2的节点,且最下面一层的叶节点集中在最左边的若干位置上。
具有n个节点的完全二叉树的深度为
(log2n)+1或 log2(n+1)。
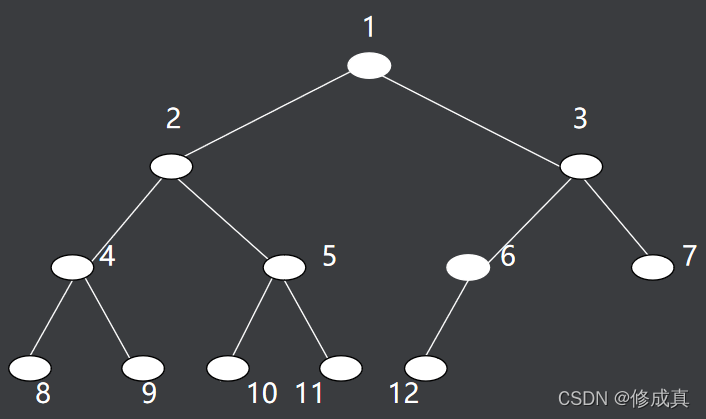
3、二叉树-顺序存储
顺序存储结构 :完全二叉树节点的编号方法是从上到下,从左到右,根节点为1号节点。设完全二叉树的节点数为n,某节点编号为i。
- 当
i>1(不是根节点)时,有父节点,其编号为i/2; - 当
2*i≤n时,有左孩子,其编号为2*i,否则没有左孩子,本身是叶节点; - 当
2*i+1≤n时,有右孩子,其编号为2*i+1,否则没有右孩子; - 当
i为奇数且不为1时,有左兄弟,其编号为i-1,否则没有左兄弟; - 当
i为偶数且小于n时,有右兄弟,其编号为i+1,否则没有右兄弟;
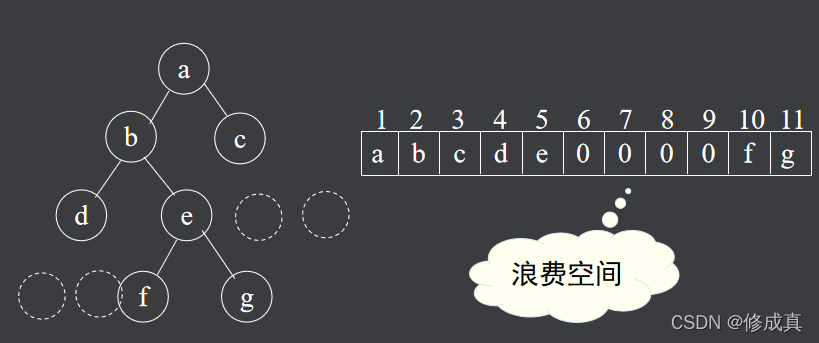
有n个节点的完全二叉树可以用有n+1个元素的数组进行顺序存储,节点号和数组下标一一对应,下标为零的元素不用。
利用以上特性,可以从下标获得
节点的逻辑关系。不完全二叉树通过添加虚节点构成完全二叉树,然后用数组存储,这要浪费一些存储空间。
4、二叉树-链式存储
示意图:
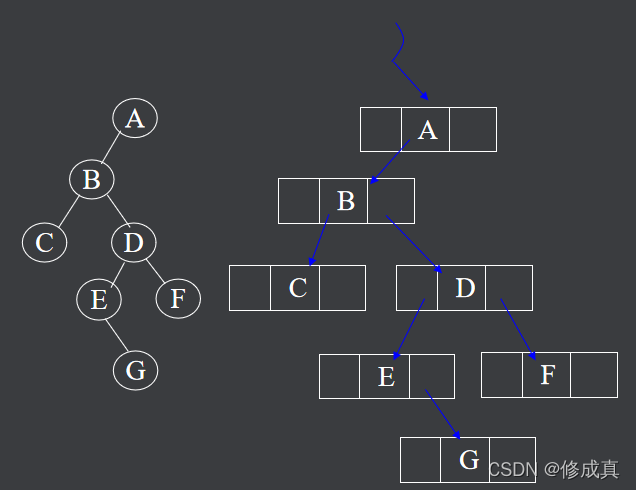
结构体定义:
typedef char datatype;
typedef struct node_t
{
datatype data; //序号
struct node_t *left_tree; //左结点指针
struct node_t *right_tree; //右结点指针
}bittree;
5、二叉树的遍历
遍历:沿某条搜索路径周游二叉树,对树中的每一个节点访问一次且仅访问一次。
二叉树是
非线性结构,每个结点有两个后继,则存在如何遍历即按什么样的搜索路径进行遍历的问题。
由于二叉树的递归性质,
遍历算法也是递归的。
三种基本的遍历算法如下 :
先序序列:先访问树根,再访问左子树,最后访问右子树;中序序列:先访问左子树,再访问树根,最后访问右子树;后序序列:先访问左子树,再访问右子树,最后访问树根;
示例:
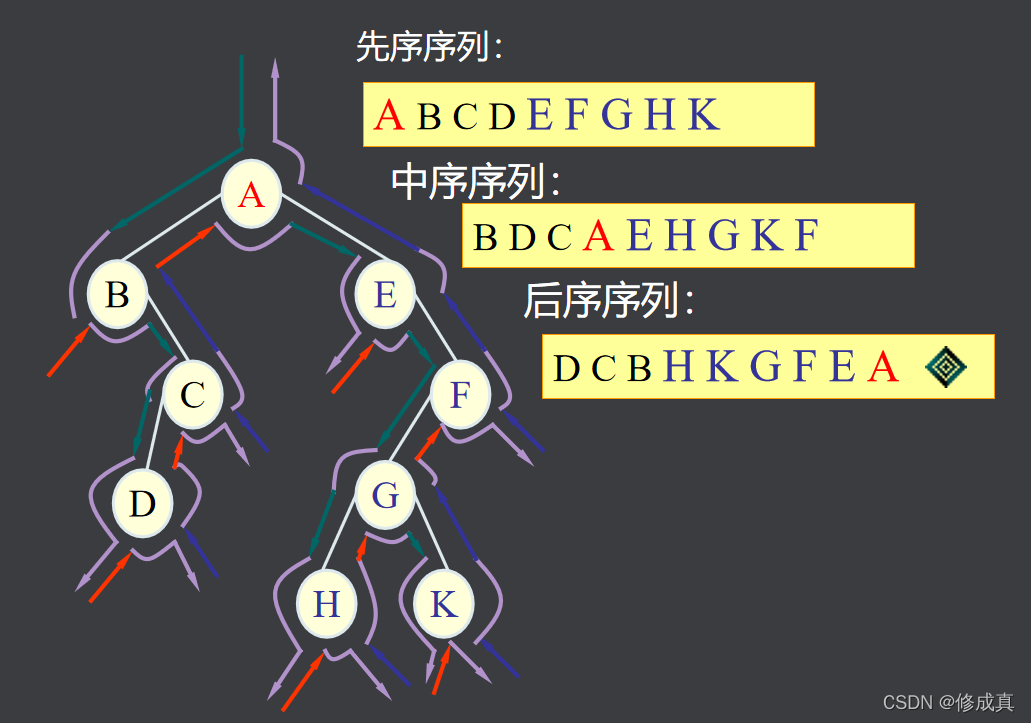
6、二叉树创建与遍历C程序的实现
(1)二叉树的创建
/**
* @description: 二叉树的创建
* @param {*}
* @return {r-二叉树根节点的地址}
*/
bittree *tree_create()
{
datatype value;
bittree *r;
scanf("%c", &value);
if(value == '#')
return NULL;
r = (bittree *)malloc(sizeof(bittree));
if(r == NULL)
{
#if DEBUG
printf("bittree create error!\n");
#endif
return NULL;
}
r->data = value;
r->left_tree = tree_create();
r->right_tree = tree_create();
return r;
}
(2)前序遍历法
/**
* @description: 前序遍历法
* @param {bittree} *r-二叉树根节点的地址
* @return {0-没有子结点时,1-函数结点}
*/
int preorder(bittree *r)
{
if(r == NULL)
return 0;
printf("%c ", r->data);
preorder(r->left_tree);
preorder(r->right_tree);
return 1;
}
(3)中序遍历
/**
* @description: 中序遍历
* @param {bittree} *r-二叉树根节点的地址
* @return {0-没有子结点时,1-函数结点}
*/
int inorder(bittree *r)
{
if(r == NULL)
return 0;
inorder(r->left_tree);
printf("%c ", r->data);
inorder(r->right_tree);
return 1;
}
(4)后序遍历
/**
* @description: 后序遍历
* @param {bittree} *r-二叉树根节点的地址
* @return {0-没有子结点时,1-函数结点}
*/
int backorder(bittree *r)
{
if(r == NULL)
return 0;
backorder(r->left_tree);
backorder(r->right_tree);
printf("%c ", r->data);
return 1;
}
(4)层数遍历
需要应用链表队列
/**
* @description: 层次遍历
* @param {bittree} *r-二叉树根节点的地址
* @return {0-函数失败,1-函数成功}
*/
int levelorder(bittree *r)
{
linkqueue lq;
if(r == NULL)
{
#if DEBUG
printf("r is NULL\n");
#endif
return 0;
}
if((lq = linkqueue_create()) == NULL)
return 0;
linkqueue_enter(lq, r);
while(!linkqueue_empty(lq))
{
r = linkqueue_out(lq);
printf("%c ",r->data);
if(r->left_tree != NULL)
linkqueue_enter(lq, r->left_tree);
if(r->right_tree != NULL)
linkqueue_enter(lq, r->right_tree);
}
puts("");
return 1;
}
三、完整程序链接
到这里就结束啦!