本文通过示例介绍R实现CART(classification and regression tree)过程。
当一组预测变量与响应变量的关系为线性时,我们使用多重线性回归可以生成准确的预测模型。但当它们的关系为更复杂的非线性关系时,则需采用非线性模型。
分类回归CART(classification and regression tree)方法使用一组预测变量构建决策树,用来预测响应变量。响应变量是连续的,我们能构建回归树;如果响应变量是分类类型,则构建分类树。下面通过示例构建回归和分类树过程。
构建回归树
我们使用ISLR包中的Hitters数据集,它包括263个专业棒球运动员的各类信息。我们将使用该数据集构建回归树,预测变量是home runs和years played ,响应变量运动员的Salary。
- 加载包
library(ISLR) # 包含 Hitters 数据集
library(rpart) # 决策树算法实现
library(rpart.plot) # 图视化决策树
- 构建初步回归树
首先构建大的初始回归树,为了让树足够大,我们使用较小的cp值(complexity parameter:复杂性参数)。这意味着指定较小的cp值,只要模型总体R方增加就继续产生新的分支。然后使用printcp()函数打印模型结果:
# 构建初始回归树
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart.control(cp=.0001))
# 查看结果
printcp(tree)
#
# Regression tree:
# rpart(formula = Salary ~ Years + HmRun, data = Hitters, control = rpart.control(cp = 1e-04))
#
# Variables actually used in tree construction:
# [1] HmRun Years
#
# Root node error: 53319113/263 = 202734
#
# n=263 (因为不存在,59个观察量被删除了)
#
# CP nsplit rel error xerror xstd
# 1 0.24674996 0 1.00000 1.00878 0.13855
# 2 0.10806932 1 0.75325 0.76404 0.12750
# 3 0.01865610 2 0.64518 0.69032 0.12187
# 4 0.01761100 3 0.62652 0.72818 0.12517
# 5 0.01747617 4 0.60891 0.72653 0.12519
# 6 0.01038188 5 0.59144 0.70819 0.12032
# 7 0.01038065 6 0.58106 0.69777 0.11848
# 8 0.00731045 8 0.56029 0.69620 0.12013
# 9 0.00714883 9 0.55298 0.69893 0.11987
# 10 0.00708618 10 0.54583 0.69754 0.11989
# 11 0.00516285 12 0.53166 0.70187 0.11974
# 12 0.00445345 13 0.52650 0.69581 0.12115
# 13 0.00406069 14 0.52205 0.69963 0.12120
# 14 0.00264728 15 0.51799 0.70416 0.12220
# 15 0.00196586 16 0.51534 0.69776 0.12096
# 16 0.00016686 17 0.51337 0.69266 0.11828
# 17 0.00010000 18 0.51321 0.69318 0.11857
- 树剪枝
下面对回归树进行剪枝,使用cp值寻找最优值(最低测试误差)。从上节输出我们看到cp的最佳值是致xerror最低的记录值,它表示交叉验证数据的观察结果的误差。
# 识别最佳CP值
best <- tree$cptable[which.min(tree$cptable[,"xerror"]),"CP"]
# 基于最佳CP值对模型树进行剪枝
pruned_tree <- prune(tree, cp=best)
# 画出剪枝后的模型树
prp(pruned_tree,
faclen=0, # 使用完整标签名称
extra=1, # 显示每个终端节点数量
roundint=F, # 输出数值不近似为整数
digits=5) # 输出显示小数位数5位
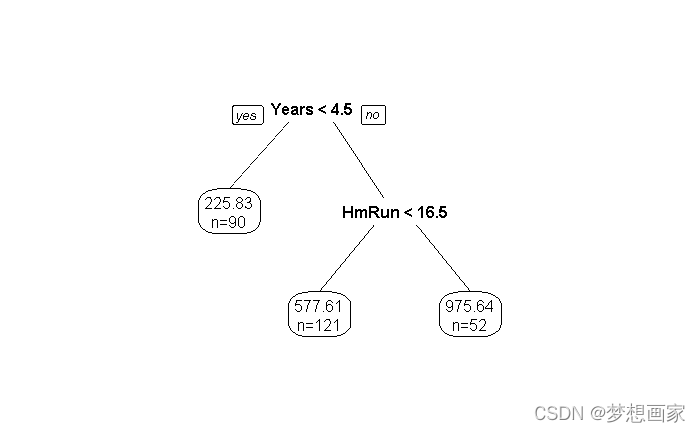
我们看到最终剪枝为3个终端节点。每个终端节点显示运动员的薪资及原始数据中属于该节点的观察记录数量。
举例,原始数据中职业经验小于4.5年的有90个运动员,薪资为$225.83k。
- 使用剪枝树进行预测
下面使用最终的剪枝树预测新的运动员薪资,基于职业经验和平均本垒(home runs). 举例,某运动员有7年职业经验,平均home runs为4,则预测薪资为:577.61k .
执行predict函数进行验证:
# 给定新的运动员信息
new <- data.frame(Years=7, HmRun=4)
# 使用剪枝树预测运动员薪资
predict(pruned_tree, newdata=new)
# 577.6061
构建分类树
这个示例使用 rpart.plot 包中的 ptitanic 数据集,它包含Titanic(泰坦尼克号)上乘客的各类信息。我们利用该信息构建分类树,使用预测变量:pclass(乘客等级), sex, 和 age,预测变量为是否存活。
- 加载包
library(rpart) # 决策树算法实现
library(rpart.plot) # 图视化决策树
- 构建初始分类树
#build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart.control(cp=.0001))
#view results
printcp(tree)
# Classification tree:
# rpart(formula = survived ~ pclass + sex + age, data = ptitanic,
# control = rpart.control(cp = 1e-04))
#
# Variables actually used in tree construction:
# [1] age pclass sex
#
# Root node error: 500/1309 = 0.38197
#
# n= 1309
#
# CP nsplit rel error xerror xstd
# 1 0.4240 0 1.000 1.000 0.035158
# 2 0.0140 1 0.576 0.576 0.029976
# 3 0.0095 3 0.548 0.580 0.030050
# 4 0.0070 7 0.510 0.550 0.029477
# 5 0.0050 9 0.496 0.524 0.028952
# 6 0.0025 11 0.486 0.534 0.029157
# 7 0.0020 19 0.464 0.538 0.029238
# 8 0.0001 22 0.458 0.528 0.029035
- 剪枝树
下面对回归树进行剪枝,使用cp值寻找最优值(最低测试误差)。从上节输出我们看到cp的最佳值是致xerror最低的记录值,它表示交叉验证数据的观察结果的误差。
# 识别最佳CP值
best <- tree$cptable[which.min(tree$cptable[,"xerror"]),"CP"]
# 基于最佳cp值进行剪枝
pruned_tree <- prune(tree, cp=best)
# 画出剪枝后的模型树
prp(pruned_tree,
faclen=0, # 使用完整标签名称
extra=1, # 显示每个终端节点数量
roundint=F, # 输出数值不近似为整数
digits=5) # 输出显示小数位数5位
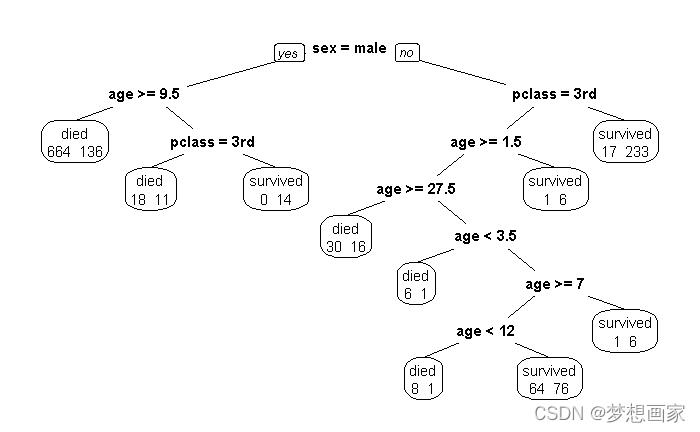
我们看到最终有10个终端节点,每个节点显示死亡和幸存乘客的数量。举例,最左边节点显示664个乘客死亡,136个乘客幸存。
- 预测
我们现在能使用最终剪枝树模型,通过pclass,age,sex变量预测给定乘客生存的概率。
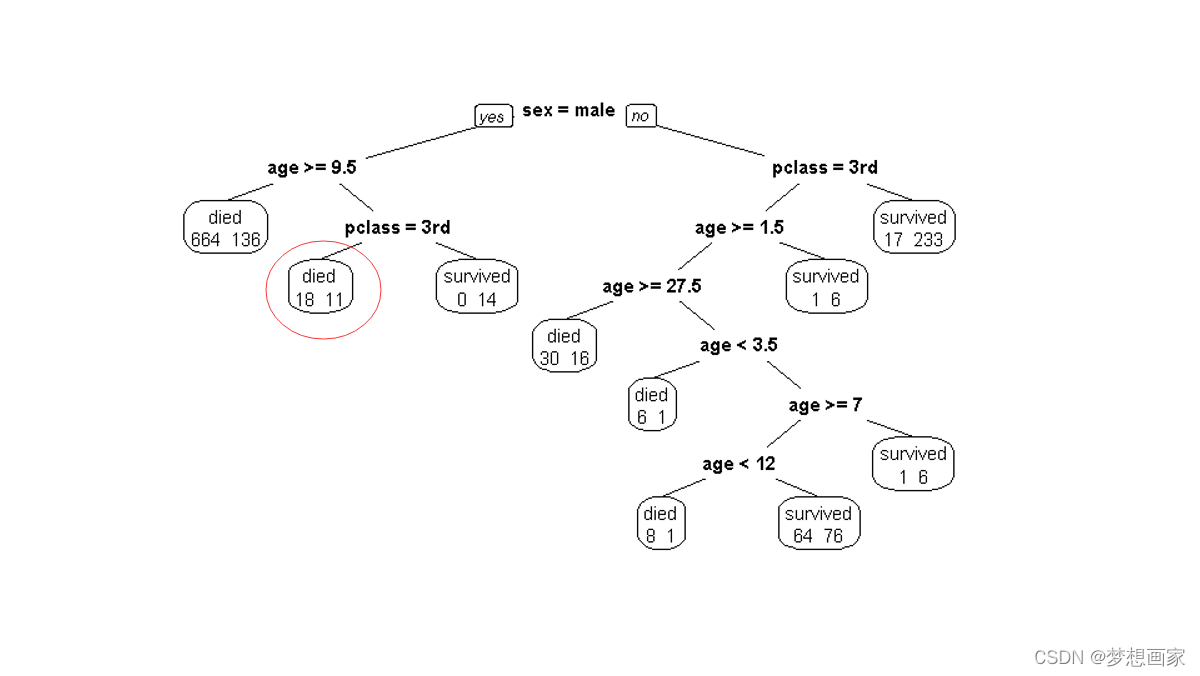
给定乘客:pclass:1st, age:8 sex:male, 则生存概率:11/29=37.9% .
总结
本文通过回归树和分类树两个示例展示决策树实现过程,希望对你有帮助。