[数据结构与算法]LeetCode 370. Range Addition - 亚马逊高频题2

You are given an integer?length?and an array?updates?where?updates[i] = [startIdxi, endIdxi, inci].

You have an array?arr?of length?length?with all zeros, and you have some operation to apply on?arr. In the?ith?operation, you should increment all the elements?arr[startIdxi], arr[startIdxi?+ 1], ..., arr[endIdxi]?by?inci.

Return?arr?after applying all the?updates.

Example 1:

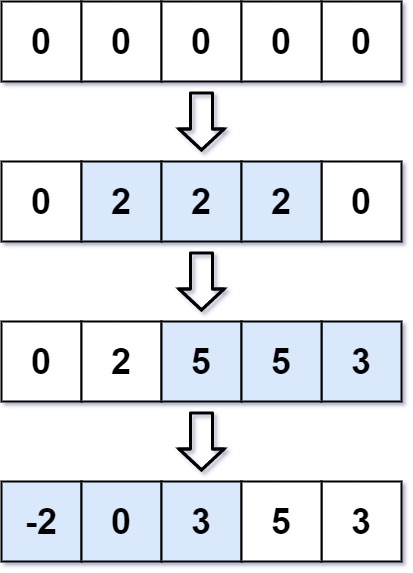
Input: length = 5, updates = [[1,3,2],[2,4,3],[0,2,-2]]
Output: [-2,0,3,5,3]

Example 2:

Input: length = 10, updates = [[2,4,6],[5,6,8],[1,9,-4]]
Output: [0,-4,2,2,2,4,4,-4,-4,-4]

Constraints:

• 1 <= length <= 105
• 0 <= updates.length <= 104
• 0 <= startIdxi?<= endIdxi?< length
• -1000 <= inci?<= 1000

题目给定一个整数length和一个数组updates，数组中每个元素含有三个信息updates[i] = [startIdxi, endIdxi, inci]。现在假定你有一个长度为length的数组arr，初始值全为0，要求你按updates给的信息更新arr对应位置值，每一次所做的操作是，把数组arr的[startIdxi, endIdxi]范围的所有值都加上值inci。

暴力解法是每次用一个for循环从startIdxi到endIdxi结束把数组arr的[startIdxi, endIdxi]范围的所有值都加上值inci。可是出题的目的显然不是要用暴力解法。

仔细再读一遍就会发现这题其实跟LeetCode 253. Meeting Rooms II??很像，对于每次updates[i] = [startIdxi, endIdxi, inci]相当于是从时间startIdxi到endIdxi结束需要inci个会议室，问最终在时间0到length-1的每个时间点上都需要多少个会议室。

?由此，我们引入时间轴概念，把数组arr中的每个位置看成一个从0到length-1的时间点，然后根据updates里信息更新每个时间点需要的会议室数量，在startIdxi时间点上需要inci个会议室即arr[startIdxi] += inci，在endIdxi时间点结束，那么下一个时间点就不需要inci个会议室了即arr[endIdxi + 1] -= inci，最后再从0到length-1扫一遍数组arr，每一个时间点所需的会议室总数就是当前点会议室数加上它前一个时间点需要的会议室数。

class Solution:
    def getModifiedArray(self, length: int, updates: List[List[int]]) -> List[int]:
        res = [0] * length
        
        for u in updates:
            res[u[0]] += u[2]
            if u[1] < length - 1:
                res[u[1] + 1] -= u[2]
        
        for i in range(1, length):
            res[i] += res[i - 1]
            
        return res

?