B+树 基本介绍
概述
Mysql 的默认储存引擎 是InnoDB,索引是储存引擎快速搜索数据的关键,而InnoDB使用的索引数据结构就是B+树。
索引使用最形象的比喻就是目录,可以帮助mysql在大量数据中定位到我们想要的数据。
今天要介绍的就是开发工作中最经常接触到的 B+树索引。
B+树本质上是指的一种数据结构,它是由二叉查找树,平衡二叉树 和 B树演化而来,要想掌握它,我们必须先了解这三种数据结构。
二叉排序树
适用场景
先看一个需求
给你一个数列 (7, 3, 10, 12, 5, 1, 9),要求能够高效的完成对数据的查询和添加
解决方案分析
-
使用数组
数组未排序, 优点:直接在数组尾添加,速度快。 缺点:查找速度慢.
数组排序,优点:可以使用二分查找,查找速度快,缺点:为了保证数组有序,在添加新数据时,找到插入位 置后,后面的数据需整体移动,速度慢。
-
使用链式存储-链表
不管链表是否有序,查找速度都慢,添加数据速度比数组快,不需要数据整体移动。
- 使用二叉排序树
二叉排序树介绍
二叉排序树:BST: (Binary Sort(Search) Tree), 对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当 前节点的值小,右子节点的值比当前节点的值大。
特别说明:如果有相同的值,可以将该节点放在左子节点或右子节点
比如针对前面的数据 (7, 3, 10, 12, 5, 1, 9) ,对应的二叉排序树为:
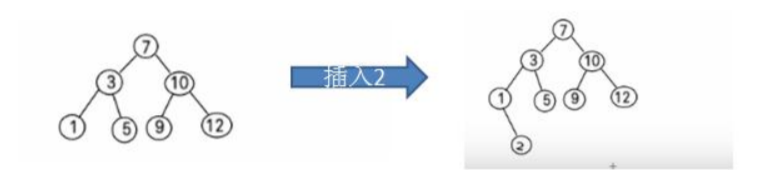
将之应用到表结构中,可以构成这样的图,可以满足对数据的快速查找和添加。

比如我们需要查询id = 12的用户,只需要从根节点出发,12 > 10 找右节点,然后 12 < 13,找右节点,三次便可找到id = 12 的节点。
平衡二叉树(AVL树)
上面我们讲解了利用二叉查找树可以快速的找到数据。但是,如果上面的二叉查找树是这样的构造:

这个时候可以看到我们的二叉查找树变成了一个链表。如果我们需要查找 id=17 的用户信息,我们需要查找 7 次,也就相当于全表扫描了。
导致这个现象的原因其实是二叉查找树变得不平衡了,也就是高度太高了,从而导致查找效率的不稳定。
平衡二叉树介绍
-
平衡二叉树也叫平衡二叉搜索树(Self-balancing binary search tree)又被称为 AVL 树, 可以保证查询效率较高。
-
具有以下特点:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵 平衡二叉树。
3)平衡二叉树就是二叉排序树的改进方式,将二叉排序树转换为平衡二叉树可加快查询效率。
平衡二叉树举例:
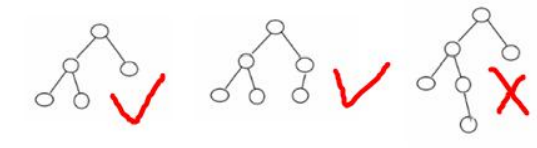
下面是平衡二叉树和非平衡二叉树的对比:

平衡二叉树的转换过程。
1.左旋转
数列 {4,3,6,5,7,8}转换为平衡二叉树
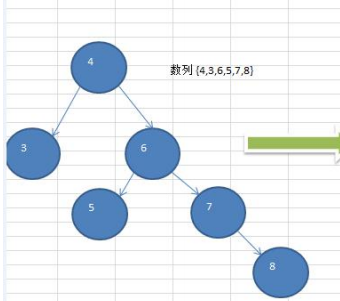
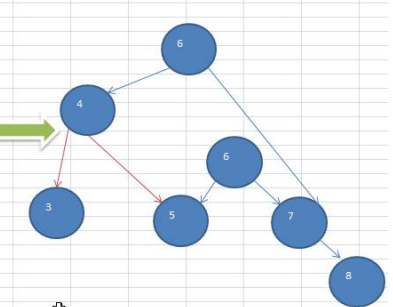
2. 右旋转
数列 {10,12, 8, 9, 7, 6}转换为平衡二叉树
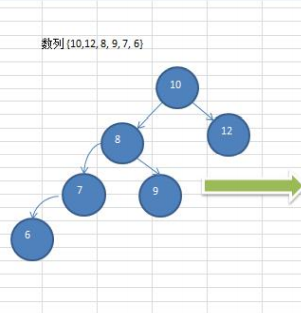
据图可知需要右旋转
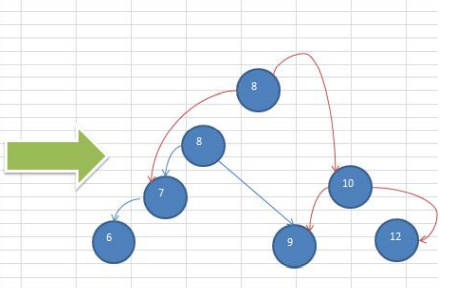
3. 双旋转
前面的两个数列,进行单旋转(即一次旋转)就可以将非平衡二叉树转成平衡二叉树,但是在某些情况下,单旋转 不能完成平衡二叉树的转换。比如数列
int[] arr = { 10, 11, 7, 6, 8, 9 }; int[] arr = {2,1,6,5,7,3};
运行原来的代码可以看到,并没有转成 AVL 树
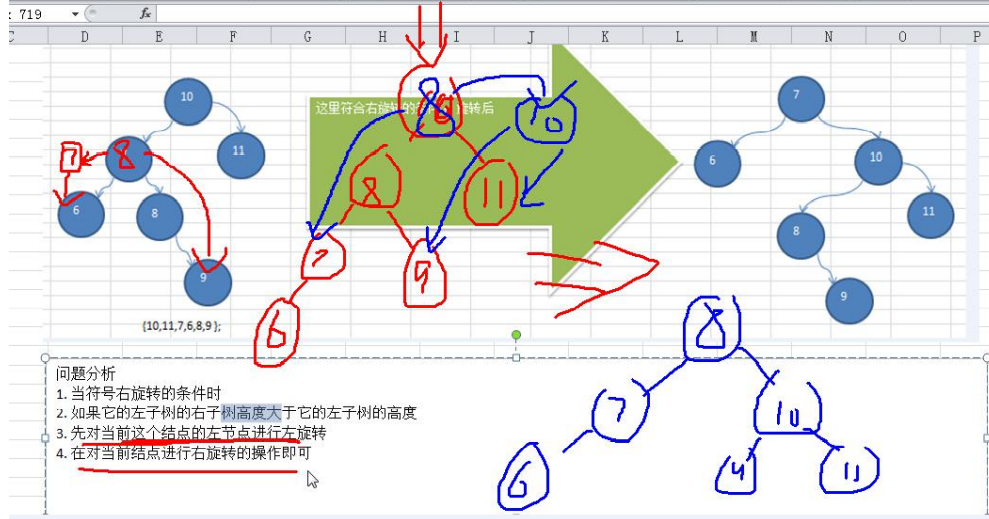
平衡二叉树保证了树的构造是平衡的,当我们插入或删除数据导致不满足平衡二叉树不平衡时,平衡二叉树会进行调整树上的节点来保持平衡。具体的调整方式这里就不介绍了。
平衡二叉树相比于二叉查找树来说,查找效率更稳定,总体的查找速度也更快。
B树
因为内存的易失性。一般情况下,我们都会选择将 user 表中的数据和索引存储在磁盘这种外围设备中。
但是和内存相比,从磁盘中读取数据的速度会慢上百倍千倍甚至万倍,所以,我们应当尽量减少从磁盘中读取数据的次数。
另外,从磁盘中读取数据时,都是按照磁盘块来读取的,并不是一条一条的读。
如果我们能把尽量多的数据放进磁盘块中,那一次磁盘读取操作就会读取更多数据,那我们查找数据的时间也会大幅度降低。
如果我们用树这种数据结构作为索引的数据结构,那我们每查找一次数据就需要从磁盘中读取一个节点,也就是我们说的一个磁盘块。
我们都知道平衡二叉树可是每个节点只存储一个键值和数据的。那说明什么?说明每个磁盘块仅仅存储一个键值和数据!那如果我们要存储海量的数据呢?
可以想象到二叉树的节点将会非常多,高度也会极其高,我们查找数据时也会进行很多次磁盘 IO,我们查找数据的效率将会极低!

为了解决平衡二叉树的这个弊端,我们应该寻找一种单个节点可以存储多个键值和数据的平衡树。也就是我们接下来要说的 B 树。
B 树(Balance Tree)即为平衡树的意思,下图即是一棵 B 树:

图中的 p 节点为指向子节点的指针,二叉查找树和平衡二叉树其实也有,因为图的美观性,被省略了。
图中的每个节点称为页,页就是我们上面说的磁盘块,在 MySQL 中数据读取的基本单位都是页,所以我们这里叫做页更符合 MySQL 中索引的底层数据结构。
页的结构我们在下文再具体介绍。
从上图可以看出,B 树相对于平衡二叉树,每个节点存储了更多的键值(key)和数据(data),并且每个节点拥有更多的子节点,子节点的个数一般称为阶,上述图中的 B 树为 3 阶 B 树,高度也会很低。
基于这个特性,B 树查找数据读取磁盘的次数将会很少,数据的查找效率也会比平衡二叉树高很多。
这里页
- 先找到根节点也就是页 1,判断 28 在键值 17 和 35 之间,那么我们根据页 1 中的指针 p2 找到页 3。
- 将 28 和页 3 中的键值相比较,28 在 26 和 30 之间,我们根据页 3 中的指针 p2 找到页 8。
- 将 28 和页 8 中的键值相比较,发现有匹配的键值 28,键值 28 对应的用户信息为(28,bv)。
(这里是为了页1 - 页8 是为了方便理解,mysql在分配页的时候并不是按照顺序分配的,很大可能页是不连续的)
B+ 树
B+ 树是对 B 树的进一步优化。让我们先来看下 B+ 树的结构图:

10 * 30 * 90 = 27000
100 * 300 * 90 =
根据上图我们来看下 B+ 树和 B 树有什么不同:
①B+ 树非叶子节点上是不存储数据的,仅存储键值,而 B 树节点中不仅存储键值,也会存储数据,
非叶子节点被称为目录项记录 上面只储存主键值和对应的页号。(存储着很多对,和叶子节点的页结构一样。)
叶子节点储存着真正的数据,每一个页的默认大小是16KB
因为非叶子节点只存主键值和对应的页号,所以能储存更多的键值,相应的树的阶数(节点的子节点树)就会更大,树就会更矮更胖,如此一来我们查找数据进行磁盘的 IO 次数又会再次减少,数据查询的效率也会更快。
② B+ 树索引的所有数据均存储在叶子节点,而且数据是按照顺序排列(页内的数据也是通过链表储存)
因为 B+ 树索引的所有数据均存储在叶子节点,而且数据是按照顺序排列的。那么 B+ 树使得范围查找,排序查找,分组查找以及去重查找变得异常简单。而 B 树因为数据分散在各个节点,要实现这一点是很不容易的。
B+ 树中各个页之间是通过双向链表连接的,叶子节点中的数据是通过单向链表连接的。
其实上面的 B 树我们也可以对各个节点加上链表。这些不是它们之前的区别,是因为在 MySQL 的 InnoDB 存储引擎中,索引就是这样存储的。
InnoDB 数据页结构
页是InnoDB管理储存空间的基本单位,一个页的大小一般是16KB。InnoDB 为了不同的目的而设计了多种不同类型的页,例如 存放表空间头部信息的页、储存Change Buffer 信息的页、存放INODE信息的页、存放undo日志的页。这里我们主要介绍储存记录的页,和储存目录项的页。
在刚才的介绍中,我们了解到B+树索引每个节点都是一个页,**叶子节点储存的是数据,我们称之为数据页,非叶子节点储存的是主键值和页号,我们称之为目录页。**我们可以把数据页理解为书本的正文内容,目录页理解为书本的目录。
InnoDB页的储存空间划分
页是InnoDB储存数据的基本单位,一个InnoDB页的储存空间被划分为7个部分:
| 名称 | 中文名 | 占用空间大小 | 描述 |
|---|---|---|---|
| File Header | 文件头部 | 38字节 | 页的一些通用信息 |
| Page Header | 页面头部 | 56字节 | 数据页专有的一些信息 |
| Infimum + Supremum | 页面中的最小记录和最大记录 | 26字节 | 两个虚拟的记录 |
| User Records | 用户记录 | 不确定 | 用户储存的记录内容 |
| Free Space | 空闲空间 | 不确定 | 页中尚未使用的记录 |
| Page Directory | 页目录 | 不确定 | 页中某些记录的相对位置 |
| File Trailer | 文件尾部 | 8字节 | 校验页是否完整 |
我们平常储存的数据就是储存在 User Records 空间中,但在一开始生成页的时候,其实并没有User Records 部分,每当插入一条记录时,都会从Free Space部分申请一个记录大小的空间,并将这个空间划分到User Records部分。当Free Space部分空间全部被User Records替代掉后,就意味着这个页空间用完了,需要申请新的页了。
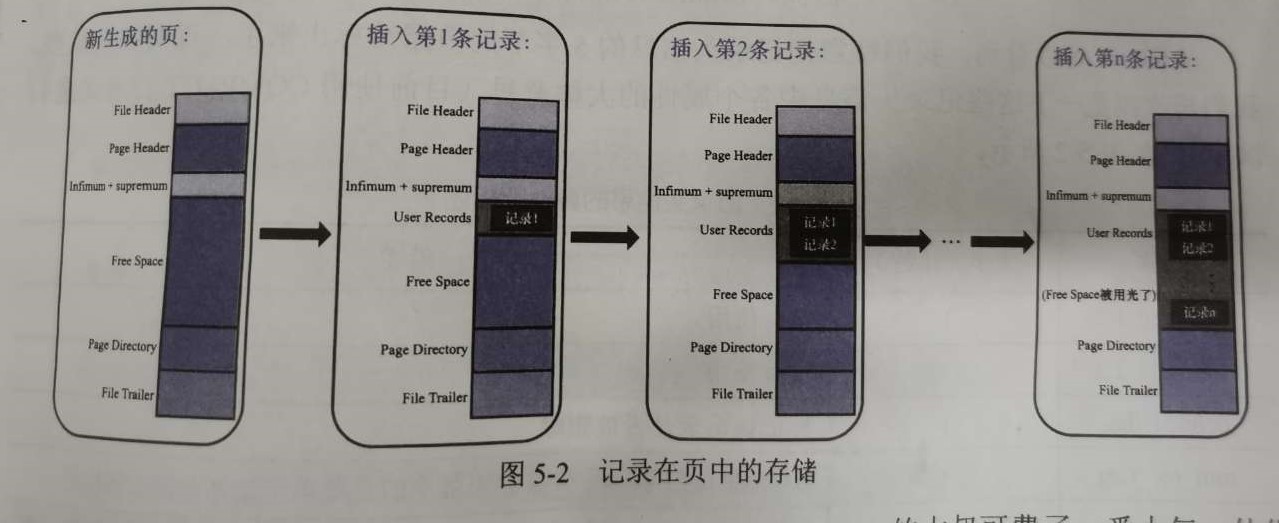
当然,记录不可能直接一条一条塞到User Records中,InnoDB 有他自己储存记录的方式,如何管理好这些杂乱无章的记录,才是最重要的。
记录头信息
要想了解记录在User Records中的储存方式,我们需要先了解下记录头的概念。
首先我们先看一张图:
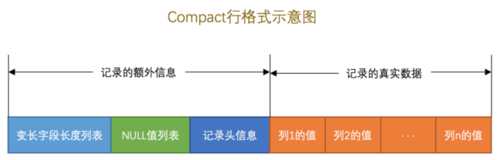
这个是一条行格式为compact的记录的行格式示意图。
这里可以先简单介绍一下compact 行格式,InnoDB中共有4中不同类型的行格式 分别是 COMPACT、REDUNDANT、DYNAMIC、COMPRESSED。
我们知道mysql是以一行记录为单位向表中插入数据的。
每行的数据除了记录我们所插入的真实数据外,InnoDB还需要记录一些额外的信息去维护这些记录。
他们分别是变长长度列表 、NULL 值列表、记录头信息。 前两者在这里我就不再介绍,有兴趣的可以看 《Mysql是怎样运行的》这本书,第四章有仔细介绍四种行格式。
在这里我想仔细说一下记录头所储存的东西,这有关于记录之间的联系。

| 名称 | 大小 | 描述 |
|---|---|---|
| 预留位1 | 1 | 没有使用 |
| 预留位2 | 1 | 没有使用 |
| deleted_flag | 1 | 标记该记录是否使用,默认为0,删除标记为1,所有被删除的记录会被组成一个垃圾链表,记录在这个链表占用的空间被称为可重用空间,如果有新的记录插入,它们可能覆盖掉被删除的这些记录占用的空间。 |
| min_rec_flag | 1 | B+树中每层非叶子节点的最小目录项都会添加该标记 |
| n_owned | 1 | 一个页面中的记录会被分成若干小组,每个组中有一个记录是“带头大哥”,其余记录都是其附属的“小弟”,n_owned记录了改组的记录条数,“小弟”们的n_owned值为0 |
| heap_no | 13 | 表示当前记录在堆中的相对位置 |
| record_type | 3 | 表示当前记录的类型,0表示普通记录,1表示B+数非叶子节点的目录项记录,2表示Infimum记录,3表示Supremum记录、 |
| next_record | 16 | 表示下一条记录的相对位置 |
我们暂时来关注三个属性,heap_no、record_type、next_record。
heap_no
我们像表中插入的记录从本质上来说都是放到数据页的UserRecords部分,这些记录一条条亲密无间的排列着。
如图:
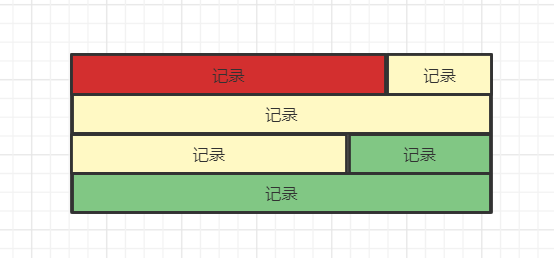
我们把这一条条亲密无间排列的结构称之为堆,为了方便管理这个堆,他们把一条条记录在堆中的相对位置称之为heap_no。我们可以模拟一下几条记录的储存图。
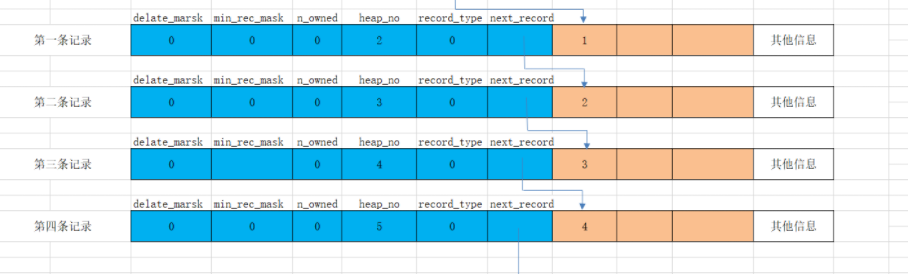
可以发现一个问题,为什么heap_no 是从 2开始的呢,0和1上哪了?这其实是InnoDB默认为我们添加了两条虚拟记录。
一条是页面中的最小记录(Infimum)
一条是页面中的最大记录 (Supremum)
为什么说他们是最大和最小记录呢,那么记录又是如何比大小的呢?
对于一条完整的记录来说,记录比较的大小就是主键的大小。但是无论我们插入了多少记录,InndoDB的都规定,任何用户记录都比Infimum大,比Supremum小。
这两条记录的构造非常简单,都是由5个字节的记录头信息和8个字节的一个固定单词组成。

-
Infimum 和 Supremum 并不储存在User_Records空间中,而是存在 一个专门的空间,就是上文我们看到的Infimum + Supremum部分。
-
Infimum 和 Supremum 的heap_no分别是0 和 1。
有一点需要特别注意,堆记录中的heap_no基本是不变的,即使被删除了,这条记录的heap_no也不会改变。
record_type
表示当前记录的类型,共有四种
- 0 普通记录
- 1 B+树非叶子节点的目录项记录
- 2 Infimum 记录
- 3 Supremum 记录
next_record
这个属性才是重点,他表示的是当前记录的真实数据到下一条记录的真实数据的距离。如果该值为正数,说明该记录的下一条记录在当前记录地址空间后面,改值为负数,说明该记录的下一条记录在当前记录地址空间的前面。
有了这个属性,就让杂乱无章的记录形成了一个链表结构,可以快速找到下一条记录的位置。
需要注意的是,下一条记录指的并不是插入记录的下一条,而是按照主键从小到大排序的下一条记录(默认情况下),而且规定infimum记录的下一条就是本页主键最小的一条记录,本页主键最大的一条记录就是 supremum。
我们可以通过如下图更明朗的看到next_record的作用
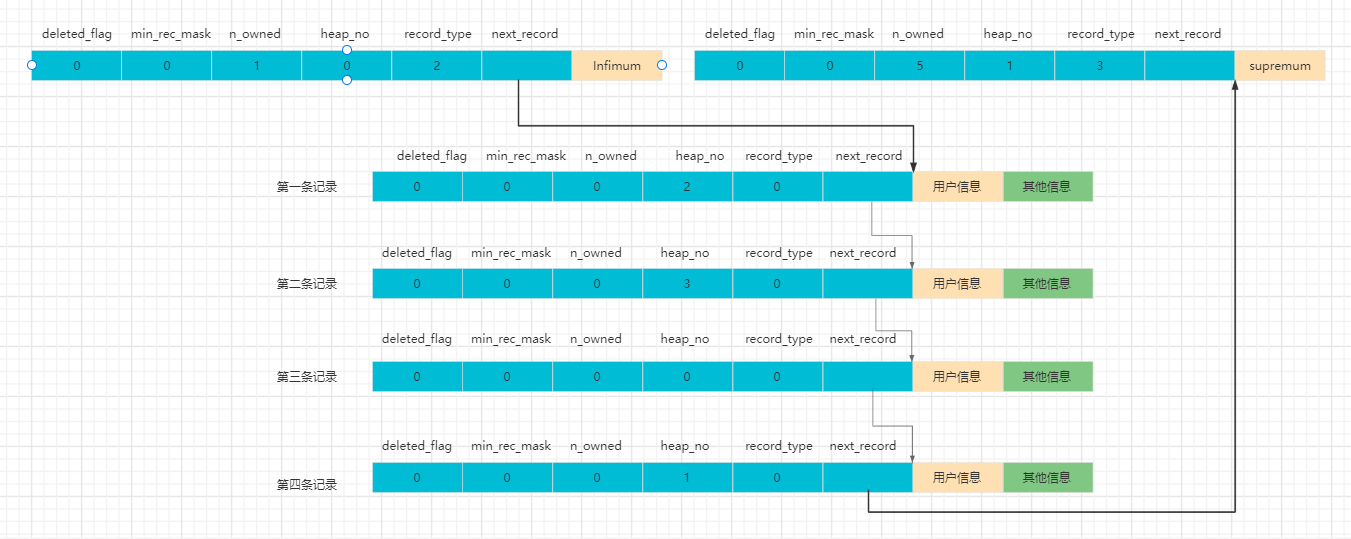
如果我们要删除第二条记录
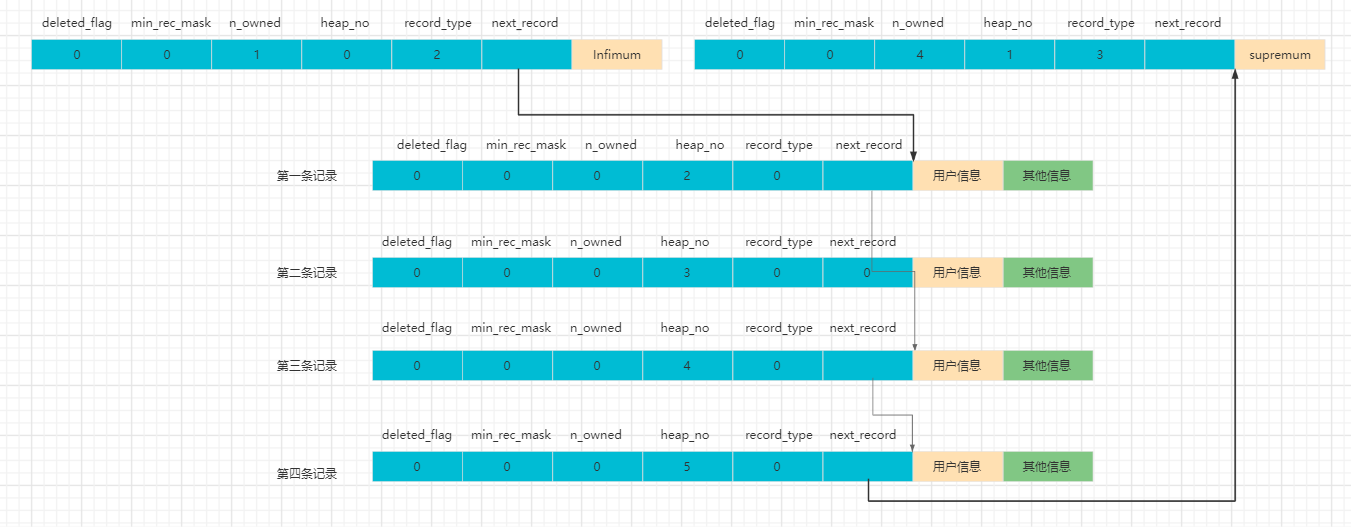
那么将发生如下改变
- 第二条记录的deleted_flag = 1,该记录储存空间仍保留着。
- 第二条记录的 next_record = 0
- 第一条记录的next_record指向了第三条记录。
- o_owned的值从 5 变成了 4。
至此,我们得出一个结论,无论对页中的记录如何操作,InnoDB始终会维护记录的一个单向链表,且各节点都是按照主键值排序的。
如果我们再插入第二条记录,则他会直接复用我们刚才删除记录的储存空间。
页目录
要想彻底弄懂InnoDB是如何快速在页内找到想要的数据,我们还需要知道一个知识点,那就是页目录。
比如我们此时想查询 id = 3 的记录(假设是上图第三条记录)我们需要怎么找呢,
按现在我们所需到的,最笨的办法就是遍历链表,一个一个找,因为每个节点都是按照id排序的。
但当数据过多时,这个方法就不太好了,InnoDB就设计了一种比较好的查询方案,模仿书的目录,建立一个页目录。
建立的具体过程:
- 将所有正常的记录划分为几个组(包括Infimum 和 Supremum记录,但不包括被删除的记录)
- 每个组的主键最大的一条记录(即最后一条记录)为“头领”,其他记录为“小弟”,“头目”记录中的n_owned属性记录改组记录数量。
- 每组“头领”在页面中的地址偏移量,按顺序储存到靠近页尾的地方。这个地方就被成为页目录,页目录的这些地址偏移量就被成为槽。
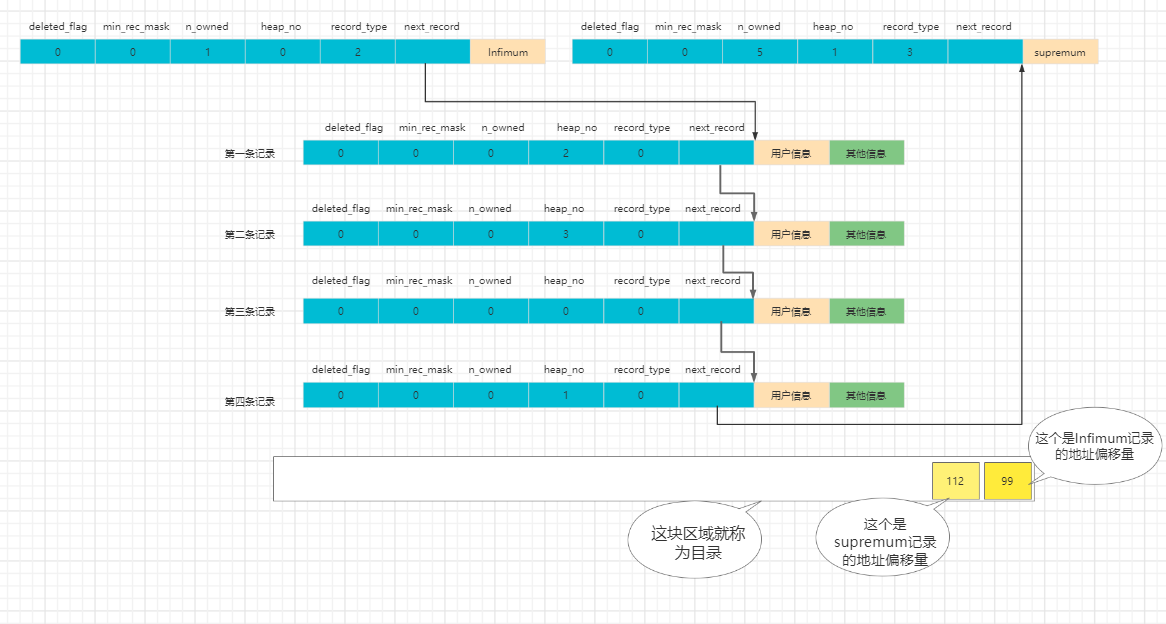
上图中,数据被分为了两个组,我们可以看到页目录中有两个槽。
同时注意 infimum和 supremum的 o_owned值,可以看到,Infimum n_owned = 1,supremum n_owned = 5,
说明Infimum组只有一个,就是他一个。
supremum 组五个,他自己和其他四条用户记录。
为什么infimum 只有一个呢?
因为InnoDB规定:对于Infimum记录所在分组只能有1条记录,而Supremum记录所在的分组拥有1~8条记录,其他的分组 为 4~8条。
在页面中一条数据没有的情况下,就会有两个分组,当插入数据大于8条时,就会将组内数据拆分成两个组,一个组中4条记录,另一个5条记录。在拆分过程中会新增一个槽,记录新增分组中最大的那条记录的偏移量。
那么有了槽,对我们查找数据有什么帮助吗?我们继续往下看。
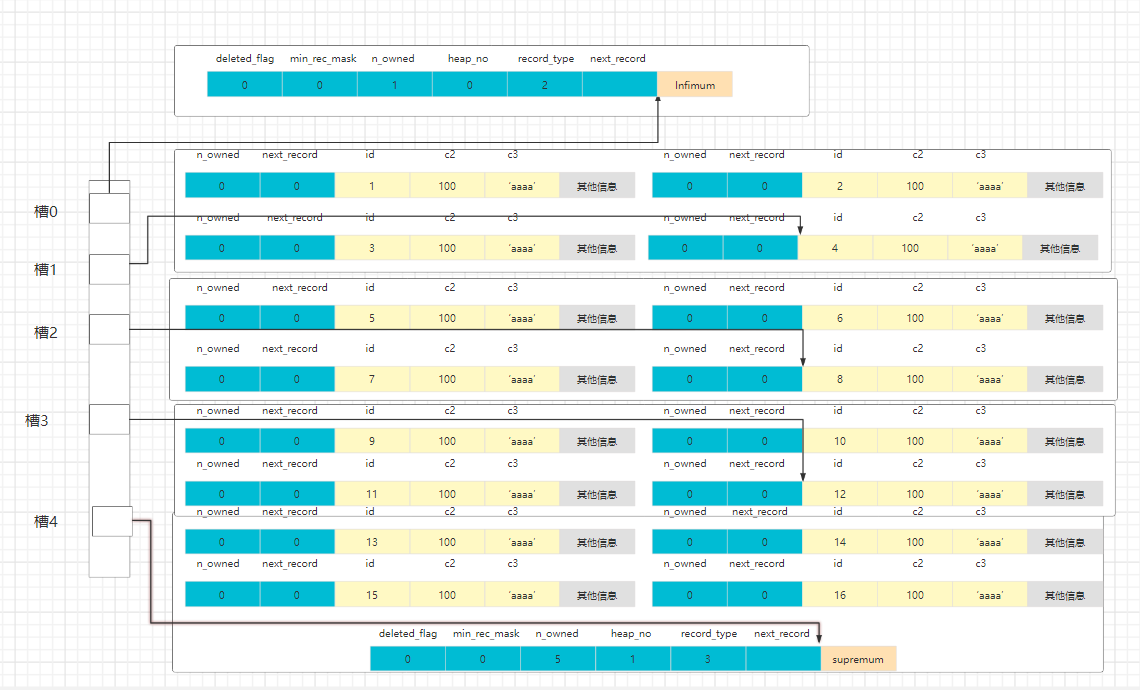
我们将行信息简化一下,得到了插入id 为1 ~16数据的页面结构图。(先不用纠结槽的位置,只是为了更清晰)
此时,如果我们想要访问id = 6 的数据,是什么步骤呢。
-
我们可以通过二分法快速定位槽的位置, (4 + 0)/2 = 2 ,所以先找2槽
-
2号槽的最后一条数据是8, 8 > 6,所以我们应该向上找,
-
我们重新计算中间槽的位置 (0+2)/ 2 = 1,槽1的最后一条数据是 4,4 < 6,说明该记录在1槽下面,
-
此时已经可以确定记录是在2槽中,但链表只能单向遍历,我们必须要找到2槽的第一条记录,
-
其实虽然数据被分为一个一个组,但数据之间还是相连的,1槽最后一个记录的下一个记录即是2槽的第一个记录,这时我们就可以,从2槽开始遍历,直到找到id = 6的数据。
综上所述,一个数据页想要查找主键值的记录时,过程可以分两步。
- 通过二分法找到分组对应的槽
- 通过记录的链表结构,遍历链表找到我们想要的记录。
InnoDB页的其他信息我也就不再过多介绍,如有请自行了解,可以看《mysql是怎样运行的》第五章。
再探InnoDB B+树索引
我们了解了InnoDB 数据页的存储结构后,再来了解InnoDB为什么要用B+树这种数据结构,就会好理解很多。
没有索引时查找数据
首先我们先探讨下如果没有这种数据结构,我们应该如何查找记录
在一个页中查找
-
以主键为搜索条件时
这跟我们上文将的一致,先在页目录中使用二分法快速定位到槽,然后再遍历该槽对应分组中的记录,即可快速找到指定的记录。
-
以其他列作为搜搜条件时
我们只能从Infimum开始遍历整个链表,知道找到我们想要的记录。
在很多页中查找
我们可以归结为两步
- 定位到记录所在的页;
- 在页内查找相应的记录
在没有索引的条件下我们不能快速的找到记录所在的位置,所以只能从第一页开始,沿着双向链表一路遍历下去。
那么此时,索引的作用就显得如此重要。