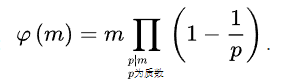[数据结构与算法]互质 计蒜客T1554

样例输入

7
12
0

样例输出

6
4

首先这个题一开始，根据数据范围分析我们使用的方法，n<1e9，那么判断是所有和它互素的数字，用正常的方法去一一判断肯定会超时，而我们学习过数论的同学都知道有一个函数叫做欧拉函数，它的值代表小于这个数并且与该数互素的数字个数，前人告诉后人一个求欧拉函数的计算方法：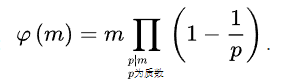

--------------------------------------------------------------------------------------------------------------------

基于此，我们利用这个公式可以求出结果。注意，在这个for循环中我们可以保证找到的第一个因子它一定是个素因子，那么我们把n中这个所有素因子全部除去，再找到的二小的因子肯定也是个素因子。

这个for循环中的循环跳出条件中的n是不断改变的，并且我们可以保证一轮循环结束后n中没有小于等于i的因子，并且此时的n还是初始n的因子之一，因此，for循环结束如果n还是一个大于1的数字，也需要把n这个素因子也算入结果中。

#include<bits/stdc++.h> 
using namespace std;
int main(){
	int n;
	while(cin>>n&&n){
		long long now=n;
		for(long long i=2;i*i<=n;i++){
			if(n%i==0){
				//cout<<i<<endl;
				now=now/i*(i-1);
				while(n%i==0){
					n/=i;
				}
			}
		}
		if(n>1) now=now/n*(n-1);
		cout<<now<<endl;
	}
	return 0;
}