目录
1.单调栈的基本概念?:
相信大家对栈都非常的熟悉?栈有一个非常鲜明的特点:先进后出
而所谓?单调栈?则是在栈的?先进后出?基础之上额外添加一个特性:从栈顶到栈底的元素是严格递增(or递减)。
1.对于单调递增栈,若当前进栈元素为 x,从栈顶开始遍历元素,把大于等于x的元素弹出栈,直接遇到一个小于?x?的元素或者栈为空为止,然x压入栈中。
2.对于单调递减栈,则每次弹出的是小于?x的元素。
以单调递增为例:
以序列:3,2,4,0,1,5
让其从左到右依次入栈:
第一步:将3压入栈中。
第二步:2入栈时发现此时栈中的元素比自己要大将栈中元素3弹出,将2入栈。
第三步:4入栈往栈的顶部看了一下栈顶的元素比我要小,好的4你可以到栈里面去。
第四步:0入栈往栈顶一看好家伙你居然比我要大,好的你可以从栈里面出去了,2,4出栈0入栈
第五步:1入栈往栈的顶部看了一下栈顶的元素比我要小,好的1你可以到栈里面去.
第六步:5入栈往栈的顶部看了一下栈顶的元素比我要小,好的5你可以到栈里面去.
2.单调栈的应用
2.1单调栈
题目描述:
分析:
1.要找到数组中每个i位置左边和右边离i最近的且比arr[i]的值要小的位置。我们可以使用单调栈来实现:栈中保存数组的下标
且保证从栈底到栈顶元素下标对应元素是从小到大的.如果我们是要找到数组中每一个 i 位置左边和右边离 i 位置最近且值比 arr[i] 大的位置,那么我们就需要保持栈从栈顶到栈底的下标i所对应的arr[i]由小到大的特性。
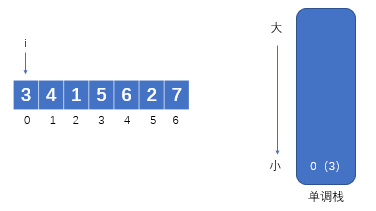
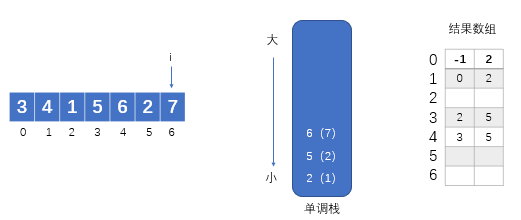
下面我们使用单调栈来求得数组arr[3 4 1 5 6 2 7]中每一个 i 位置左边和右边离 i 位置最近且值比 arr[i] 小的位置:
1.当数组遍历到0号小标时,发现栈为空,直接将下标0压入栈中即可,如下图所示:
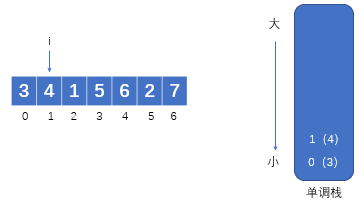
?2.当数组遍历到1号下标时发现栈顶元素3比我小,好的你可以进栈了,1进栈.如图所示:
?3.接着数组遍历到2号位时,发现arr[2]小于栈顶元素即数组的下标1所对应的数组元素4,那么直接弹出栈顶元素1,那么 1 位置左边和右边离 1 位置最近且值比 arr[1] 小的位置分别为新的栈顶0和当前的i = 2,并记录在结果数组中。若当前位置i其左边和右边不存在比arr[i]最近且比其小元素,那么就默认位置为-1。重复上述过程,直到栈为空或者arr[2]大于栈顶下标所对应的数组元素时直接压入i。该过程的结果如图所示
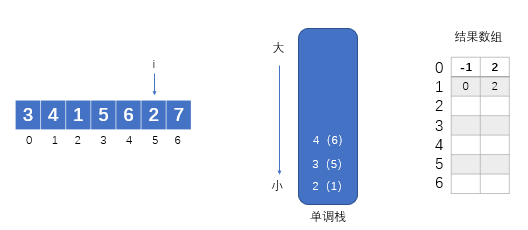
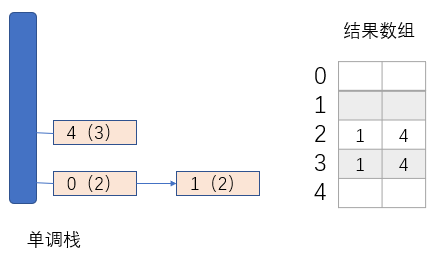
?当数组从3号位遍历到4号时,会将数组元素5和6所对应的下标压入栈中。如下图示:
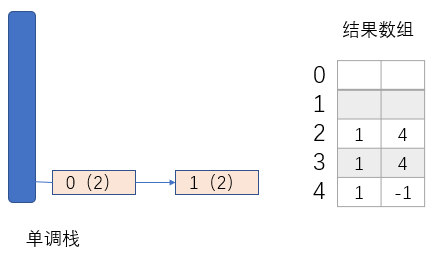
?当数组遍历到5号位时,发现arr[5]小于栈顶中元素4所对应的数组元素6,那么弹出栈顶元素并记录其左右比arr[5]小且最近的元素的下标。同理,新的栈顶也会被弹出。然后压入元素2的下标5。如下图示:
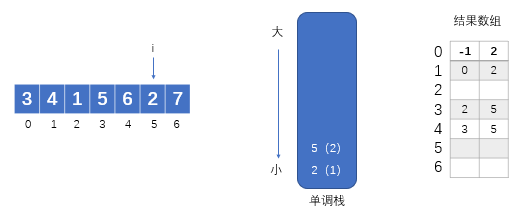
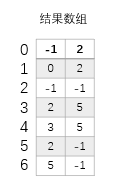
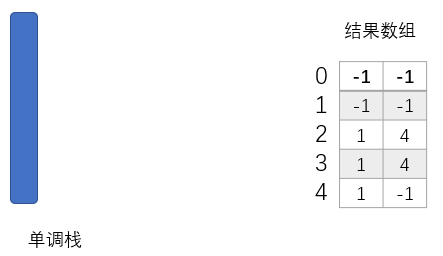
?当数组遍历到6号位时,发现arr[6]大于栈顶元素5所对应的arr[5],即2,那么直接压入下标6。自此,数组遍历结束,栈和结果数组的状态如下图所示:
?接着,我们循环的弹出栈顶元素idx,并记录arr[idx]的左边和右边最近且比arr[idx]小的元素下标,我们可以发现左边最近且比arr[idx]小的元素的下标为新的栈顶元素(若不存在则为-1),右边最近且比arr[idx]小的元素的下标不存在,即为-1。最后我们得到如下结果数组:
对应代码:
#include<iostream> #include<stack> #include<vector> using namespace std; int main(){ int n; cin>>n; vector<int>arr(n); for(int i=0;i<n;i++){ cin>>arr[i]; } stack<int>stk; vector<vector<int>>ans(n,vector<int>(2));//保存答案 for(int i=0;i<n;i++){ while(!stk.empty()&&arr[stk.top()]>arr[i]){ int cur=stk.top(); stk.pop(); int leftIndex=stk.empty()?-1:stk.top();//左边比它小的 //右边比它小的就是当前的下标i ans[cur][0]=leftIndex; ans[cur][1]=i; } stk.push(i); } while(!stk.empty()){ int rightIndex=-1;//结算阶段右边一定没有比当前数要小的 int cur=stk.top();//当前位置可以结算 stk.pop(); int leftIndex=stk.empty()?-1:stk.top();//看当前位置下面是否还压着数 ans[cur][0]=leftIndex; ans[cur][1]=rightIndex; } //打印结果 for(int i=0;i<n;i++){ printf("%d %d\n",ans[i][0],ans[i][1]); } }
?2.2单调栈进阶
题目描述:
分析本题和上题不一样的是有重复的元素:那么就有可能入栈的元素和当前栈顶的元素相等那么当前栈顶元素右边比它小的无法正确的结算。
所以此时我们需要对单调栈的结构进行改造:将栈中存在下标的整型改成链表单调性依然不变。下面以这组数据为例:数组arr[2,2,4,4,3]
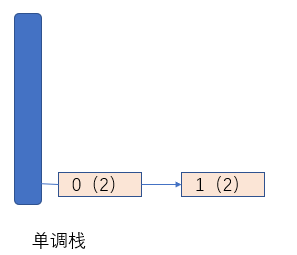
1.当遍历到数组的0号位时,由于栈为空,那么将下标0添加进链表中,然后将链表压入栈中;
当遍历到数组的1号位时,发现栈不为空,且因为arr[1]等于链表元素0所对应的arr[0],即都等于2,那么则将下标1添加进栈顶的链表中,如下图示:
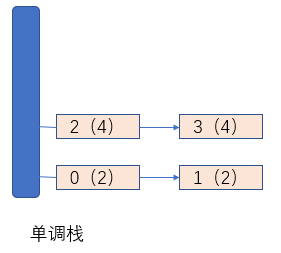
2.接着数组遍历到2号时,发现arr[2]大于栈顶链表元素0所对应的arr[0],那么直接将下标2添加进新的链表中,然后将链表压入栈中。另外,当数组遍历到3号位时同当遍历到数组的1号位时的情况一样,如下图示:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
当数组遍历到4号位时,发现arr[4]小于栈顶链表元素2所对应的arr[2],那么则将栈顶的链表弹出,然后遍历该链表,我们可以知道链表中的每个元素idx所对应的arr[idx]的左边和右边离其最近且小于arr[idx]的元素的下标分别为新的栈顶链表最右的元素(这里是3)和当前遍历到的数组元素的下标(这里是4)。然后重复上述过程,直到arr[4]小于或等于新的栈顶链表元素idx所对应的arr[idx]才停止。
如果arr[4]等于新的栈顶链表元素idx所对应的arr[idx]时,那么就将arr[4]添加到该栈顶链表中,否则就将arr[4]添加进新的链表,然后再将该链表添加进栈中。由于arr[4]不等于栈顶链表元素2所对应的arr[2],那么我们将arr[4]添加进新的链表,然后再将该链表添加进栈中。如图所示:
?接下来我们开始循环的弹出栈中的链表,然后遍历该链表,我们可以知道链表元素4所对应的arr[4]的左边离其最近且小于arr[4]的元素的下标为新的栈顶链表最右的元素的下标1,右边的则不存在,默认为-1。
我们继续弹出栈顶链表,然后遍历该链表。我们发现无新的栈顶,那么我们说明当前链表元素idx所对应的arr[idx]左边无离其最近且小于arr[idx]的元素,我们默认下标为-1,而右边的也不存在,默认为-1。
?对应代码:
#include<iostream> #include<vector> #include<stack> #include<list> using namespace std; int main(){ int n; cin>>n; vector<vector<int>>ans(n,vector<int>(2));//保存答案 vector<int>arr(n); stack<list<int>>stk;//栈中存储链表 for(int i=0;i<n;i++){ cin>>arr[i]; while(!stk.empty()&&arr[i]<arr[stk.top().front()]){ //不满足单调性 list<int>tmp=stk.top();//当前节点可以结算了 stk.pop(); int leftIndex=stk.empty()?-1:stk.top().back();//左边比他小的元素下标 for(auto x:tmp){ ans[x][0]=leftIndex; ans[x][1]=i;//右边比他小的下标对应的元素就是当前的i } } if(!stk.empty()&&arr[stk.top().front()]==arr[i]){ //如果相等加入栈顶元素的链表中 stk.top().push_back(i); } else{ stk.push({i}); } } while(!stk.empty()){//结算阶段右边比他小的没有了 list<int>tmp=stk.top(); stk.pop(); int leftIndex=stk.empty()?-1:stk.top().back(); for(auto x:tmp){ ans[x][0]=leftIndex; ans[x][1]=-1; } } //输出结果 for(int i=0;i<n;i++){ printf("%d %d\n",ans[i][0],ans[i][1]); } }
?2.3最大矩形面积
题目描述:
?解题思路:
本题的解题思路:
利用单调栈,求每个柱子作为矩形高度时的面积,取最大。
即要找到左右两侧比该柱子矮的两个柱子的坐标(最近的),面积为两侧矮柱子之间的宽度乘以该柱子的高度。
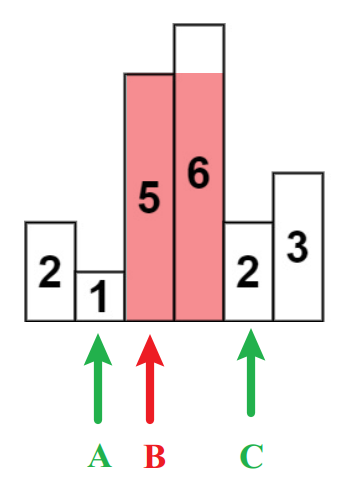
如图,柱子B两侧比它矮的最近的柱子为柱A、C,则以柱子B为矩形高度时的面积为
(C坐标-A坐标-1) * B高度
特殊情况:
1、所求柱子左侧无比它矮的,则计算宽度时,将上述公式的 A坐标 改为 -1 计算即可
2、所求柱子右侧无比它矮的,则计算宽度时,将上述公式的 C坐标 改为 heights.length 计算
对应代码:
class Solution { public: int largestRectangleArea(vector<int>& arr) { stack<int>stk; int Maxans=0;//记录答案 for(int i=0;i<arr.size();i++){ while(!stk.empty()&&arr[i]<=arr[stk.top()]){//等于 int cur=stk.top(); stk.pop(); int leftIndex=stk.empty()?-1:stk.top();//看自己底下是否压着东西 int curArea=(i-leftIndex-1)*arr[cur]; maxans=max(maxans,curArea);//看是否需要更新答案 } stk.push(i); } //结算阶段 while(!stk.empty()){ int j=stk.top(); stk.pop(); int leftIndex=stk.empty()?-1:stk.top(); int curArea=(arr.size()-leftIndex-1)*arr[j]; //当前的面积 maxans=max(maxAns,curArea); } return maxans; } };注意这里如果遇到相等的元素可以将其从栈中弹出虽然弹出的结果没用算对但是进来了一个和它一样的只要它算对了即可。
?2.4最大矩形
?题目描述:
?分析:
暴力枚举:枚举每个左上角和每个右下角,复杂度是O(n^2)*O(n^2),再枚举这个区域内是否存在0,复杂度为O(n^2),总共的时间复杂度为O(n^6)。过不了的
方法二单调栈:
我们可以枚举:子矩阵必须以第0行做地基的情况下那个子矩阵包含的1最多,在枚举子矩阵必须以第1行做地基的情况下那个子矩阵包含的1最多,重复上述过程答案一定在其中
2.5统计全为1的子矩阵数量
?
解题思路:
参考上一题的解题思路,必须以第0行做地基的情况下子矩阵全为1的个数,必须以第1行做地基的情况下子矩阵全为1的个数.重复上述过程最后不就求出来了吗?利用的技巧和上题一样空间压缩。
假设我们将其压缩为一个这样的直方图我们要求其子矩阵全为1的数量,首先对于b来说现找到左边比它小的和右边比它小的一共有多少个呢?假设5到6之间的长度为n一共有(n*(n+1)/2)*(5-2)个。为什么不是减1呢那是因为他之前已经算过了。
对应代码:
class Solution { public: int numSubmat(vector<vector<int>>& mat) { int res=0; vector<int>height(mat[0].size()); for(int i=0;i<mat.size();i++){ for(int j=0;j<mat[0].size();j++){//枚举第i行做地基子矩阵组中全为1的个数 height[j]=mat[i][j]==0?0:height[j]+1; } res+=countFromBottom(height); } return res; } int countFromBottom(vector<int>&height){ int nums=0; stack<int>stk; for(int i=0;i<height.size();i++){ while(!stk.empty()&&height[stk.top()]>=height[i]){ int cur=stk.top(); stk.pop(); if(height[cur]>height[i]){//如果和你相等后面再算法 int leftIndex=stk.empty()?-1:stk.top(); int n=i-leftIndex-1; int down=max(leftIndex==-1?0:height[leftIndex],height[i]);//取两者中最小的一个后面同一算 //最小的那个的时候统一算 nums+=num(n)*(height[cur]-down);//总的方法 } } stk.push(i); } while(!stk.empty()){ int cur=stk.top(); stk.pop(); int leftIndex=stk.empty()?-1:stk.top(); int n=height.size()-leftIndex-1; int down=leftIndex==-1?0:height[leftIndex]; nums+=(height[cur]-down)*num(n); } return nums; } int num(int n){//根据数学方法计算 1+2+....n return (n*(n+1))>>1; } };