写在前面
大噶好哇,我是秋刀鱼,因为要复习考研的内容所以现在码代码的时间越来越少了,不过这也无法磨灭了一个即将秃顶的程序员热爱代码的心,去NND考研我要开摆!
不知不觉呢蓝桥杯每日打卡的第七天了,因为今天LeetCode题目还有打卡题目还算简单所有有时间来写写题解,希望看完后能对你在做题上能有所帮助。?( ′・?・` )比心

相乘
解题思路:
枚举区间 [ 1 , 1000000007 ] [1,1000000007] [1,1000000007]的所有数值,如果该值乘2021后取余1000000007 后值为 999999999 ,输出并返回。
public class Main {
public static void main(String[] args) {
long num = 0;
for (long i = 1; i <= 1000000007; i++) {
if (i * 2021 % 1000000007 == 999999999) {
num = i;
System.out.println(num);
return;
}
}
}
}
空间
解题思路:
这里需要知道计算机的基础知识: 1 M B = 1024 K B = 1024 ? 1024 B = 1024 ? 1024 ? 8 b i t 1MB = 1024 KB = 1024*1024B = 1024*1024*8 bit 1MB=1024KB=1024?1024B=1024?1024?8bit
计算机中常说的"位"也就是bit单位,所以算出
256
M
B
256MB
256MB共有多少个位。因为不需要考虑其他的因素,所以直接将位数目除以32就是存储32位二进制整数的数量。
注意溢出,要使用long long 型数据存储结果。
#include <iostream>
using namespace std;
int main()
{
cout<<256L*1024*1024*8/32;
return 0;
}
发现环
解题思路:
一道典型的双向拓扑排序问题,如果不了解拓扑排序的小伙伴一定要自行学习后再做这道题。
- 定义
inNode[]存储每一个节点的入度,因为网络路径是双向路径,因此在添加一条新的路径时,路径两端的点入度都需要加上一 - 定义
arr[][]存储路径,arr[from][0]=to || arr[from][1] =to都能表示from节点与to节点相连接- 为什么需要的是一个二维数组呢?因为路径中增加了一条线路,导致必定会有一个结点与两个结点相连接,因此使用一个二维数组来存储
对于拓扑排序,定义一个队列存储遍历的元素,首先将入度为1的边缘结点放入队列中,并使其入度减小1,随后在队列中取出结点的索引,遍历该结点相连的结点,使其入度减小1,如果入度为1则将该相连的结点加入队列中,最终入度>1的结点,也就是没有被存入队列的结点,就是环中的结点。
// 1:无需package
// 2: 类名必须Main, 不可修改
import java.io.*;
import java.util.LinkedList;
import java.util.Queue;
public class Main {
public static void main(String[] args) throws IOException {
PrintWriter writer = new PrintWriter(new OutputStreamWriter(System.out));
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(reader);
in.nextToken();
int n = (int) in.nval;
int[][] arr = new int[n + 1][2];
int[] inNode = new int[n + 1];
for (int i = 1; i <= n; ++i) {
in.nextToken();
int to = (int) in.nval;
in.nextToken();
int from = (int) in.nval;
// 入度+1
inNode[to]++;
inNode[from]++;
// 保存方向
if (arr[from][0] != 0) {
arr[from][1]=to;
}else{
arr[from][0] = to;
}
if (arr[to][0] != 0) {
arr[to][1]=from;
}else{
arr[to][0] = from;
}
}
Queue<Integer> queue = new LinkedList<>();
for (int i = 1; i <= n; ++i) {
// 将入度为1的元素放入队列
if (inNode[i] == 1) {
queue.add(i);
inNode[i]--;
}
}
while (!queue.isEmpty()) {
int cur = queue.poll();
// 遍历其相邻结点
for (int t = 0; t <= 1; ++t) {
int nx = arr[cur][t];
if (nx != 0) {
arr[cur][t] = 0;
inNode[nx]--;
if (inNode[nx] == 1) {
queue.add(nx);
}
}
}
}
for (int i = 1; i <= n; ++i) {
if (inNode[i] > 1) {
writer.print(i + " ");
}
}
writer.flush();
}
}
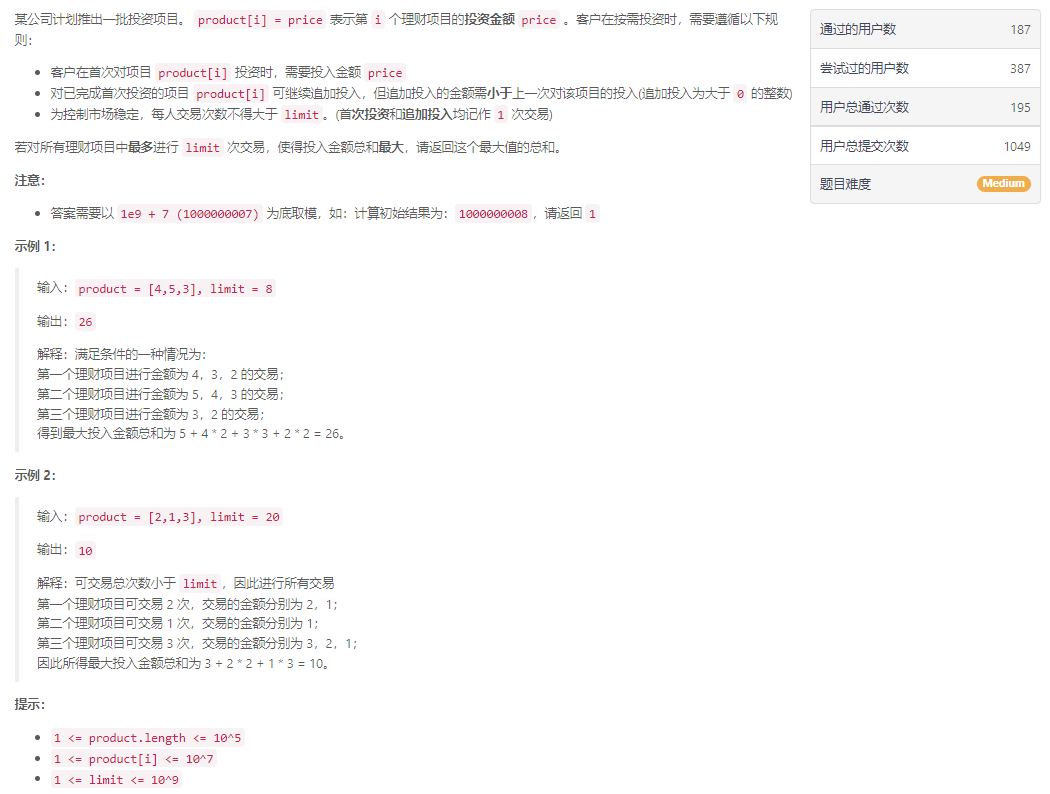
LeetCode 周赛 银联-03. 理财产品
好久没有看leetCode周赛的题目了,昨天也是没有时间所以没能够参加,今天抽空看了看后两道题,看到第四题的通过率低的离谱直接选择放弃,看了看第三题还是有些把握,于是乎就有了第三题的题解。
其实这道题还算是一道简单的模拟题,读题是想到可以使用优先队列取回、放入的操作实现,但是一看limit的范围 [ 1 , 1 0 9 ] [1,10^9] [1,109]好家伙直接排除,想了想还是只有模拟的方法靠谱。
为了使投入的金额总和最大,那么根据贪心的思想每次参与的项目一定是投资金额最大的项目,因此我们可以将product中的数据进行一个排序,大的值放在后面,那么我们优先拿后面的元素一定是符合题意的。
但是只拿最后一个元素远远不够,因为一个项目被投入后其资金会减小1,因此核心思想是:尽可能多的拿取最大值,那么最后一个元素一定是最大值时,会有一个临界值,该值就是当最后的元素值与次最大值相等时,此时我们可以选择拿取最后一个元素与次最大值。
那么为了记录排序后前一个元素与后一个元素的差值,我们定义一个差值数组gap来存储差值,
g
a
p
[
i
]
=
p
r
o
d
u
c
t
[
i
+
1
]
?
p
r
o
d
u
c
t
[
i
]
gap[i]=product[i+1]-product[i]
gap[i]=product[i+1]?product[i],定义最后一个元素gap值为0。
拿数据 【2,4,5,6,8】来举例,那么那么gap数组的值为:【2,1,1,2,0】
开始时候,拿取最后元素值,直到与次最大值相同,也就是拿取【8,7】,此时数组为:【2 4 5 6 6】
因为最大值6有两个项目,那么这时我们再拿取就是【6,6】,此时数组为【2 4 5 5 5】
此时最大值5有三个项目,那么此时我们再拿取就是【5,5,5】,此时数组为【2 4 4 4 4】
此时最大值4有四个项目,那么此时我们再拿取就是 【4,4,4,4】【3,3,3,3】,数组为【2,2,2,2,2】
不知道你有没有发现规律,就是拿取一次后,下一次可拿取的数量每次都会增加1,也就是最大值是原来拿取最大值+1,且每次能够拿取到的最小值,就是次最大值+1, 能拿取的值【最大值,最大值-1,最大值-2,…,次最大值+1】
-
定义
idx指向次最大值的索引 -
定义
num为可以拿取的最大数量,也就是数组中最大值的数量 -
定义
gapNum最大值到次最大值的差值
那么此时编写cost函数用于消费limit,具体细节看注释。
class Solution {
final long MOD = 1000000007;
long ans = 0;
long limit;
public void cost(long num, long value,long gapNum) {
// 可用拿下本轮所有值
if (limit >= num * gapNum) {
// 等差数列求和公式
ans += num * ((long) (value + (value - gapNum + 1)) * gapNum / 2);
limit -= num * gapNum;
}
// 无法拿下所有值
else {
// 能够投入的组数,例如【4,4,4,4】就是一组,【3,3,3,3】也是一组,
long groupSize = limit / num;
// 剩余无法投入完一组但是能投入剩下的部分,例如【2,2,2,2】中消费【2,2】
long restSize = limit % num;
// 剩余部分投入的值
long restValue = value - groupSize;
// 等差数列求和公式
ans += num * ((value + (long) (value - groupSize + 1)) * groupSize / 2);
ans += (long) restValue * restSize;
limit=0;
}
ans %= MOD;
}
public int maxInvestment(int[] product, int limit) {
long n = product.length;
this.limit = limit;
long[] gap = new long[(int) n];
Arrays.sort(product);
for (int i = 0; i < n - 1; ++i) {
gap[i] = product[i+1] - product[i];
}
long idx = n - 2;
while (idx >= 0 && this.limit > 0) {
// 递减数
long gapNum = gap[(int) idx];
// 当前可用最大值
long value = product[(int) (idx + 1)];
// 个数
long num = n - 1 - idx;
cost( num, value, gapNum);
ans %= MOD;
--idx;
}
// 判断如果 limit > 0
if (this.limit > 0) {
// gapNum = product[0] ,因为最小值到0,所以与次最小值0的差为改值本身
// num = n
// value = procduct[0] 因为此时剩下的项目金额均相同,最大值是product[0]
cost(n, product[0], product[0]);
}
return (int) ans;
}
}