[数据结构与算法]838. 堆排序

堆是一棵完全二叉树。

手写一个堆，实现：

1. 插入一个数。 $O(logn)$
2. 求集合中的最小值。 $O(1)$
3. 删除最小值。 $O(logn)$
4. 删除任意一个元素 。 $O(logn)$
5. 修改任意一个元素。 $O(logn)$

其中4,5 STL 中的priority_queue无法直接实现。

一维数组求堆。x的左儿子， 2 * x，x的右儿子 2 * x+1。

1. down $O(logn)$和 up $O(logn)$ 操作维护一个小根(大根)堆。

2. 下标从1开始，因为0*2还是0

1. 插入一个数。

   堆的最后一个位置插入 x 。

   heap[++size]=x,up(size);
   

2. 求集合中的最小值。

   heap[1]
   

3. 删除最小值。

   用堆的最后一个元素覆盖第一个元素，然后down(1)
   heap[1]=heap[size]
   size--;
   down(1);
   

4. 删除任意一个元素 。

   heap[k]=heap[size];size--;
   不用讨论更新后的值是变大了还是变小了，up和down只会操作一次。
   down(k);
   up(k);
   

5. 修改任意一个元素。

   heap[k]=x;
   down(k);
   up(x);
   

6. 建立一个堆：

   1. $O(nlogn)$ n个数每次使用插入操作。

      void up(int u){
          while(u>1&&h[u]>h[u/2]){//小根堆
              swap(h[u],h[u/2])
              u/=2;
          }
      }
      for(int i=1;i<=n;i++){
          h[i]=x;
          up(x);
      }
      
      

   2. $O(n)$ 输入完整数数组之后，down 一遍

      void down(int u){ // 写的不熟练
          if(u*2>n)return ;//叶节点
          int t = u;
          if(u*2<=sz&&h[t]>h[u*2]){//注意是sz不是n   !!! 写错多次 
              t=u*2;
          }
          if(u*2+1<=sz&&h[t]>h[u*2+1]){
              t=u*2+1;
          }
          if(u!=t){
      	    swap(h[u],h[t]);        
              down(t);
          }
      }
      for(int i=1;i<=n;i++){
          h[i]=x;
      }
      for(int i=n/2;i;i--)down(i);
      

   一个完全二叉树，非叶子节点是 n/2 (下取整) ， 叶子节点是 n - n / 2

   for(int i=n/2;i;i--)down(i);
   所以的叶子节点因为没有子孙不用down调整。 
   

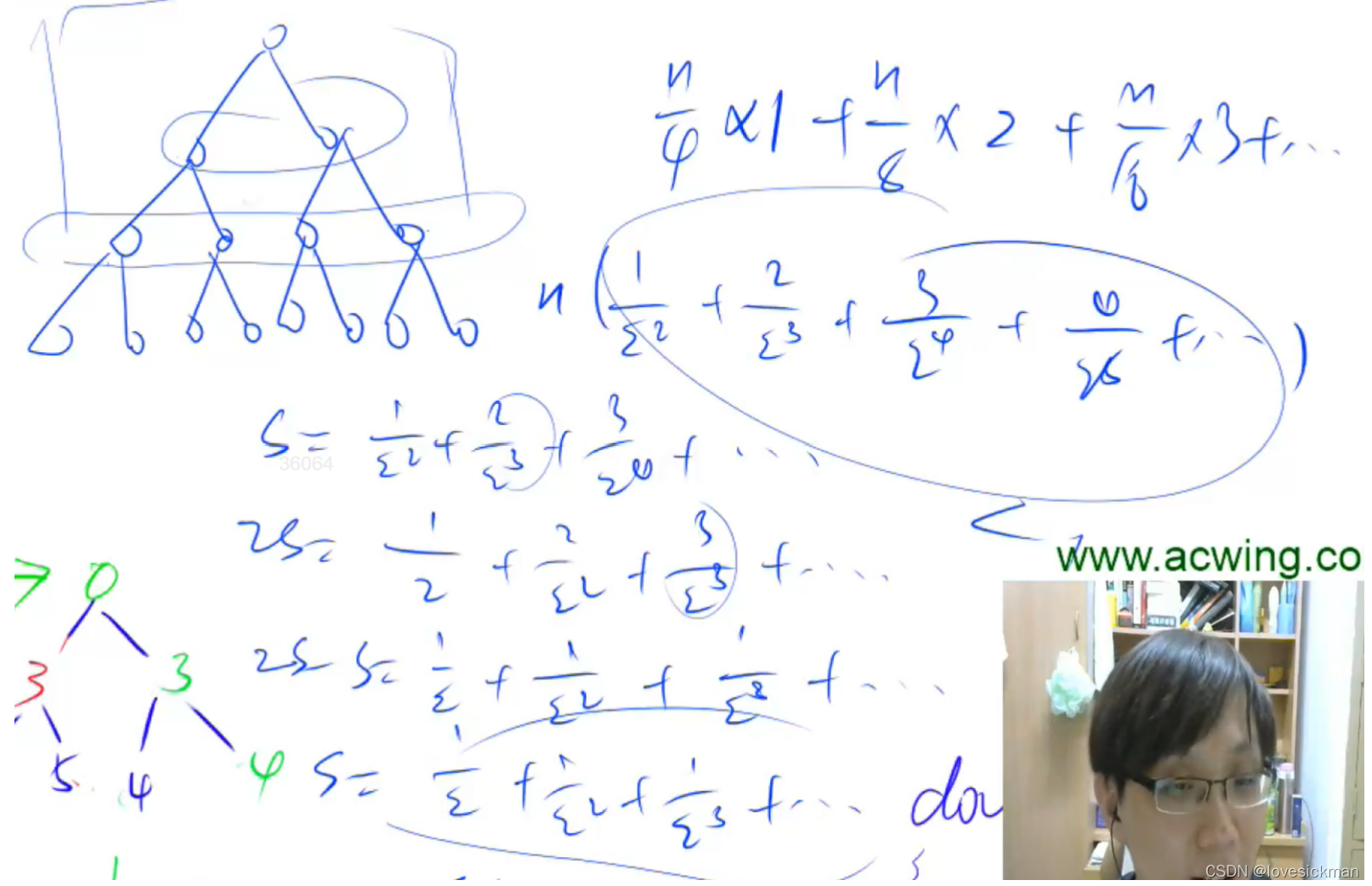
倒数第二层 n/4 节点，down一次，倒数第二层 n/8 节点，down两次，…,

第一次挑战模式：失败！2022年3月14日19点36分

#include<iostream>
using namespace std;
const int N=1e5+10;
int h[N],n,m,sz;

int down(int u){
    int t = u;
    if(u*2<=n&&h[u*2]<h[u])t = u*2;
    if((u*2+1)<=n&&h[u*2+1]<h[t])t = u*2+1;
    if(t!=u){
        swap(h[u],h[t]);
        down(t);
    }
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        int x;cin>>x;
        h[++sz]=x;
    }
    for(int i=n/2;i;i--)down(i);
    while(m--){
        cout<<h[1]<<" ";
        h[1]=h[sz];
        sz--;
        down(1);
        // sz--;
    }
}

错误原因：

int down(int u){
    int t = u;
    if(u*2<=n&&h[u*2]<h[u])t = u*2; // 应该是if(u*2<=sz&&h[u*2]<h[t]) t = u*2;
    if((u*2+1)<=n&&h[u*2+1]<h[t])t = u*2+1;// 应该是if(u*+1<=sz&&h[u*2+1]<h[t])t = u*2 +1
    if(t!=u){
        swap(h[u],h[t]);
        down(t);
    }
}