[数据结构与算法]红黑树【自平衡的二叉搜索树】

首先

红黑树虽然本质上是一棵二叉查找树，但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡，从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。加快检索速率。

AVL 数的平衡是指左右节点的高度的绝对值不能超过1，而红黑树的平衡界定是指左右节点的深度不超过1倍。

红黑树的5个性质：

1. 节点的颜色只能是红色或者黑色；
2. 根节点是黑色的；（根性质）
3. NIL 节点的颜色是黑色；
4. 如果节点的颜色是红色，则其子节点均为黑色；（红性质）
5. 从任一节点到其后代任一叶子节点的路径上的黑色节点的数量相同；（黑性质）

红黑树的旋转：

• 如果你插入的时候只有一个父结点那么就不要任何操作直接插入即可
  

• 右右型RR：先左旋再变色

  如何判断是RR型，那么就要看刚插入的结点在爷爷结点的左边还是右边，如果是右边那么就是右右型，左边就是左左型
  

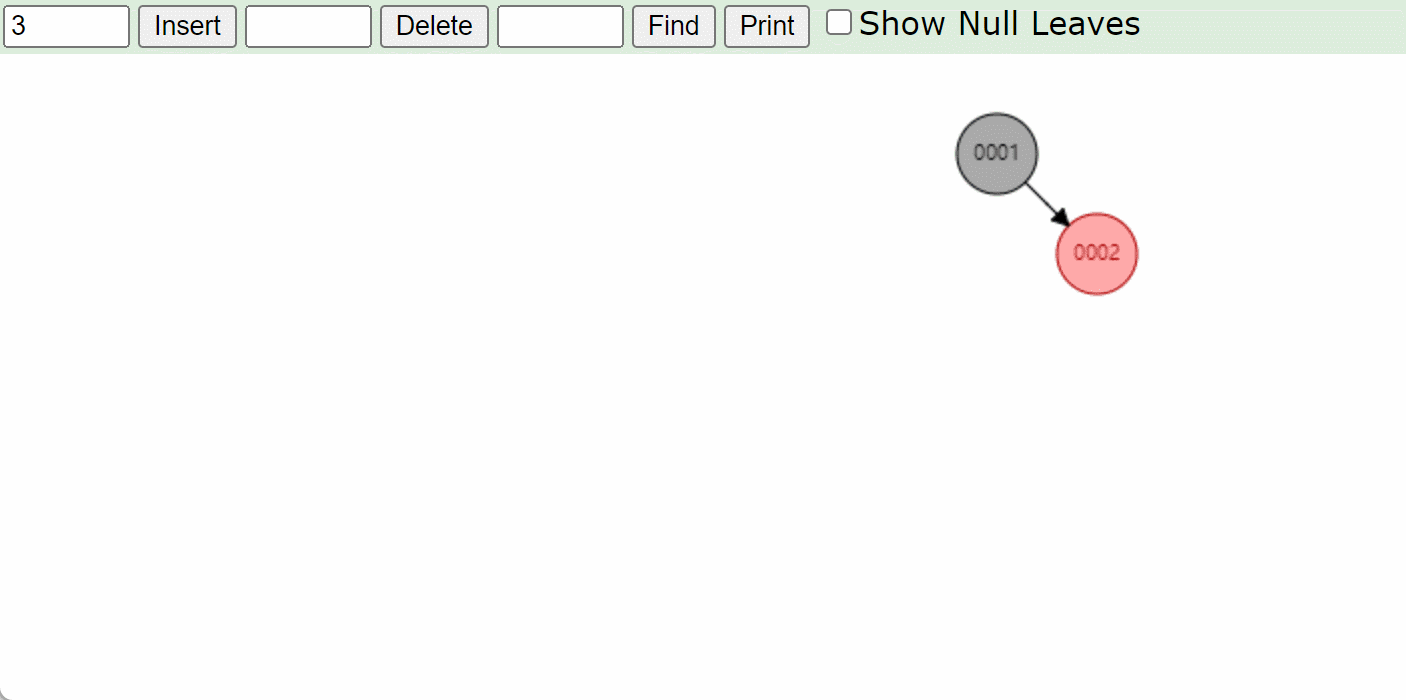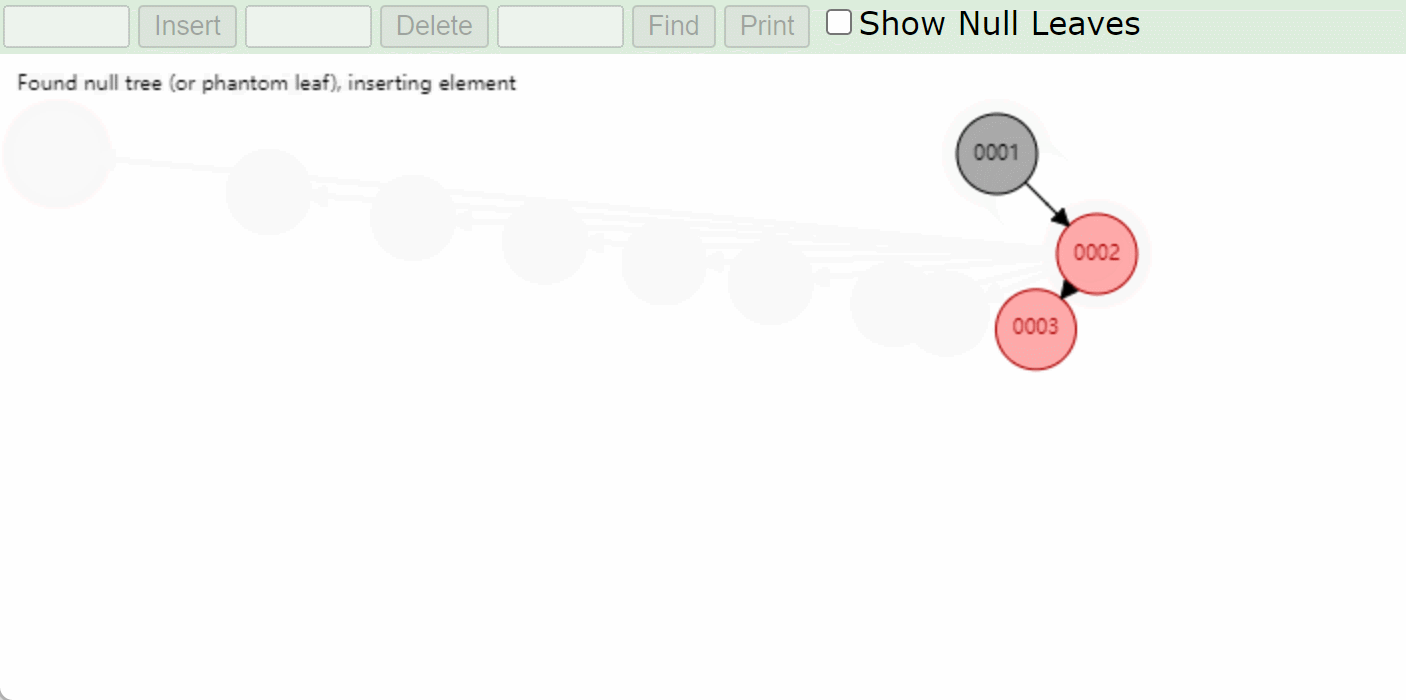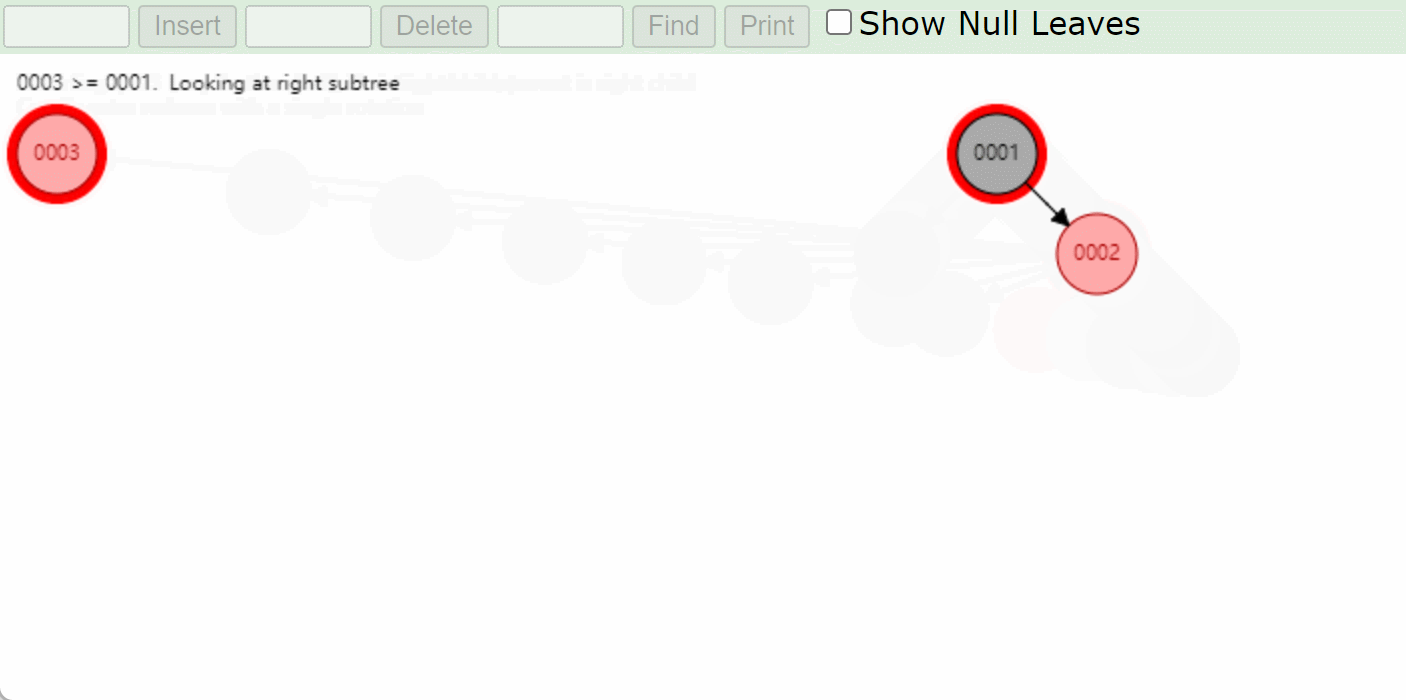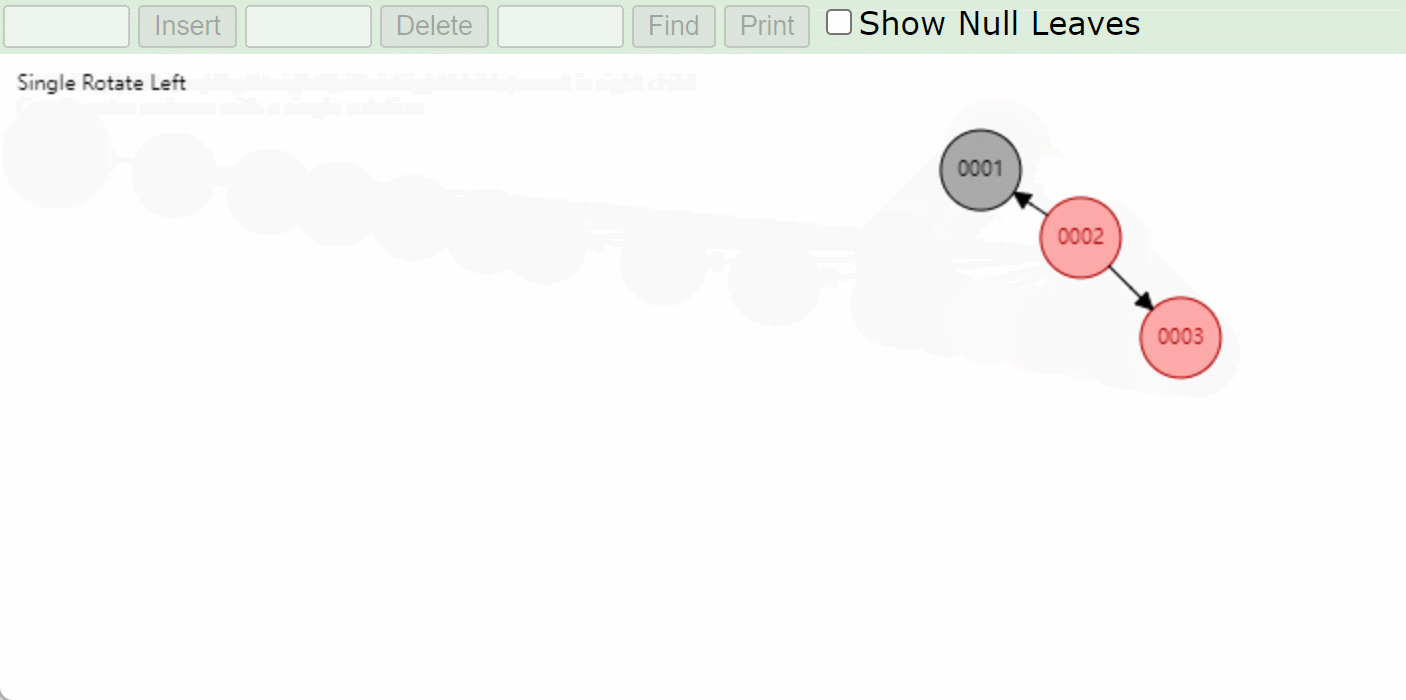
• 父结点和叔叔结点都是红色的：父叔结点都要变黑，祖父变红。祖父变成当前节点，因为根结点不能为红所以就把他变成黑。
  

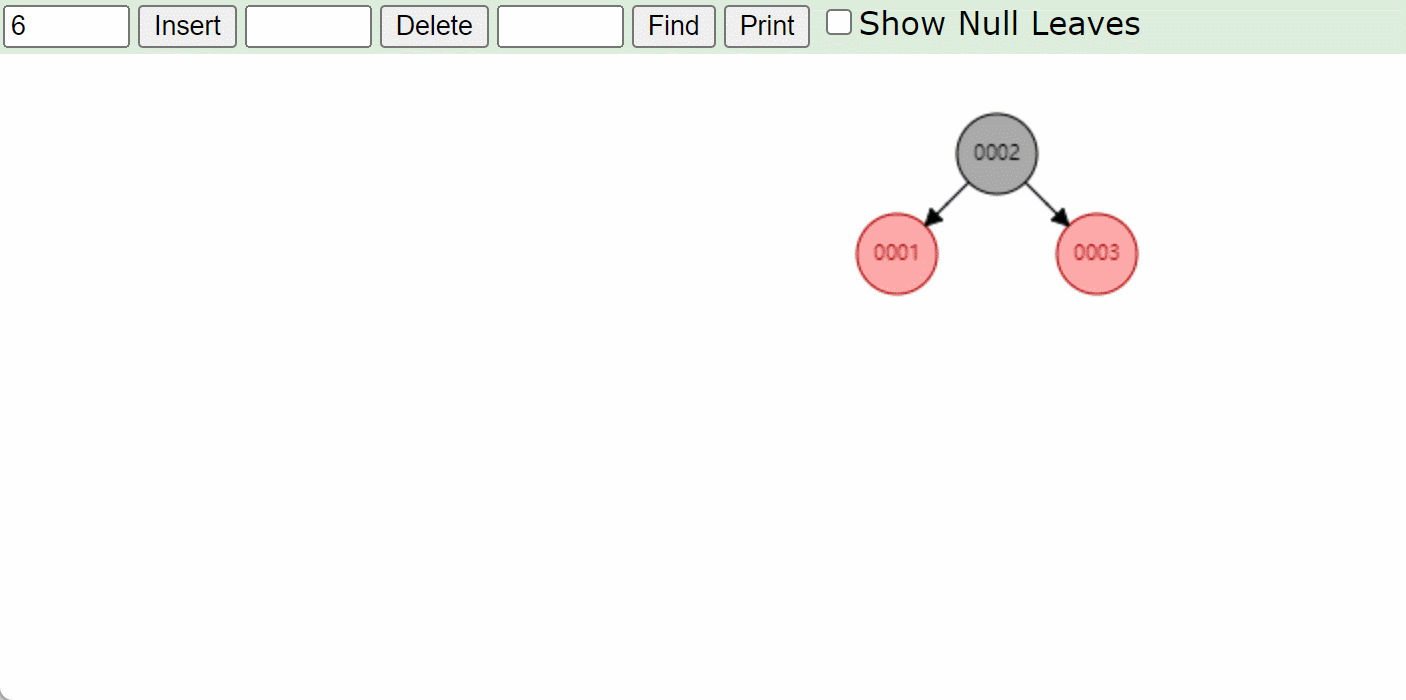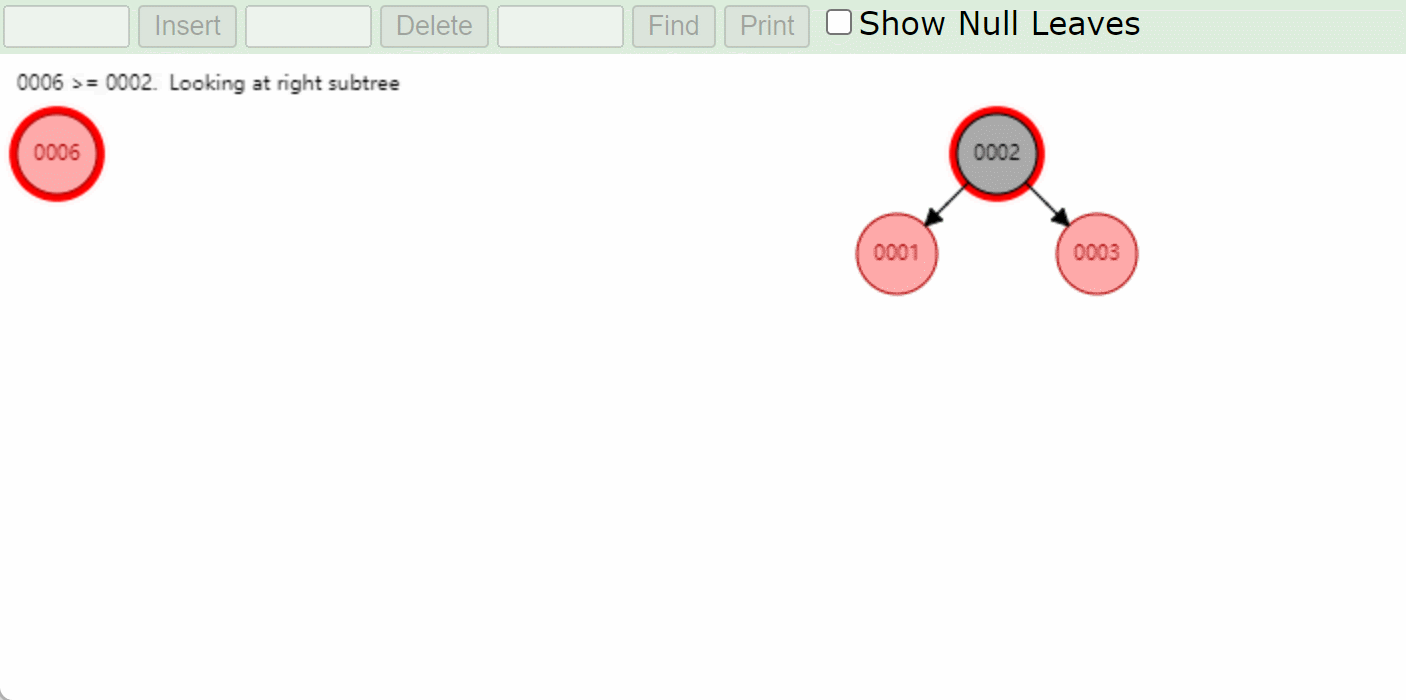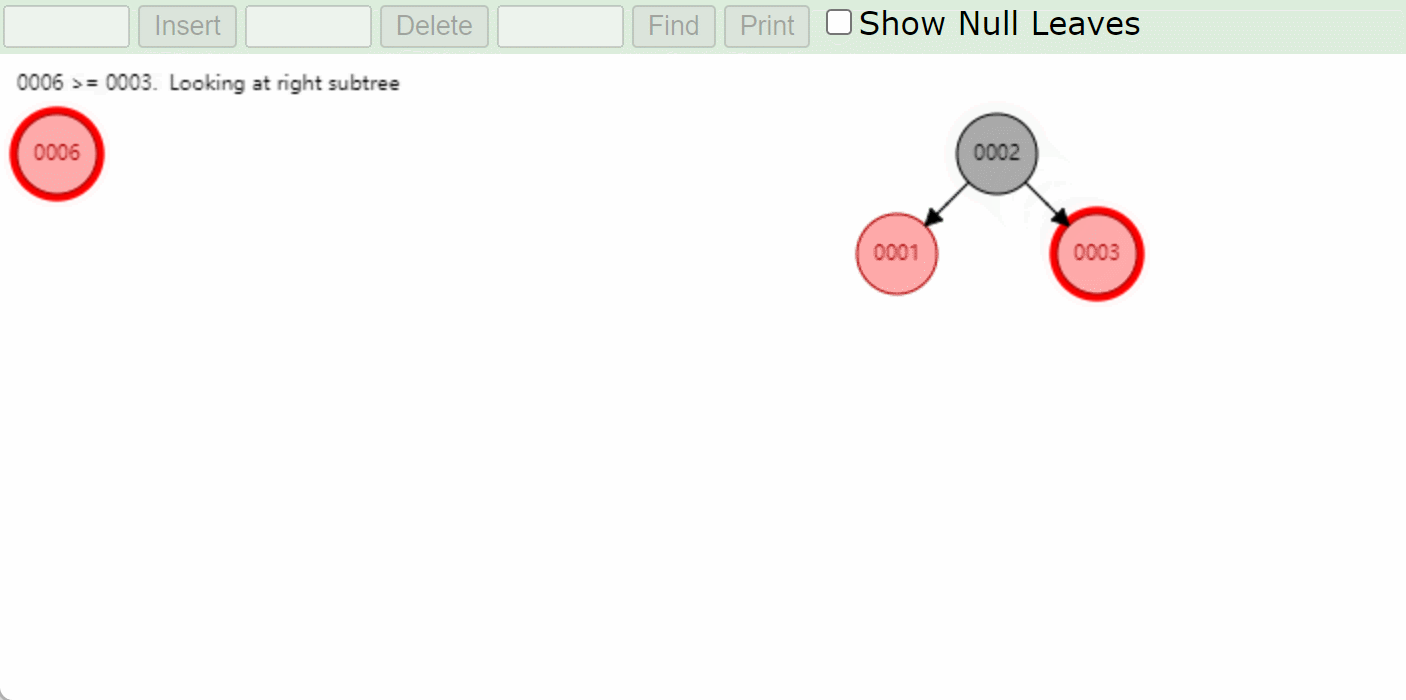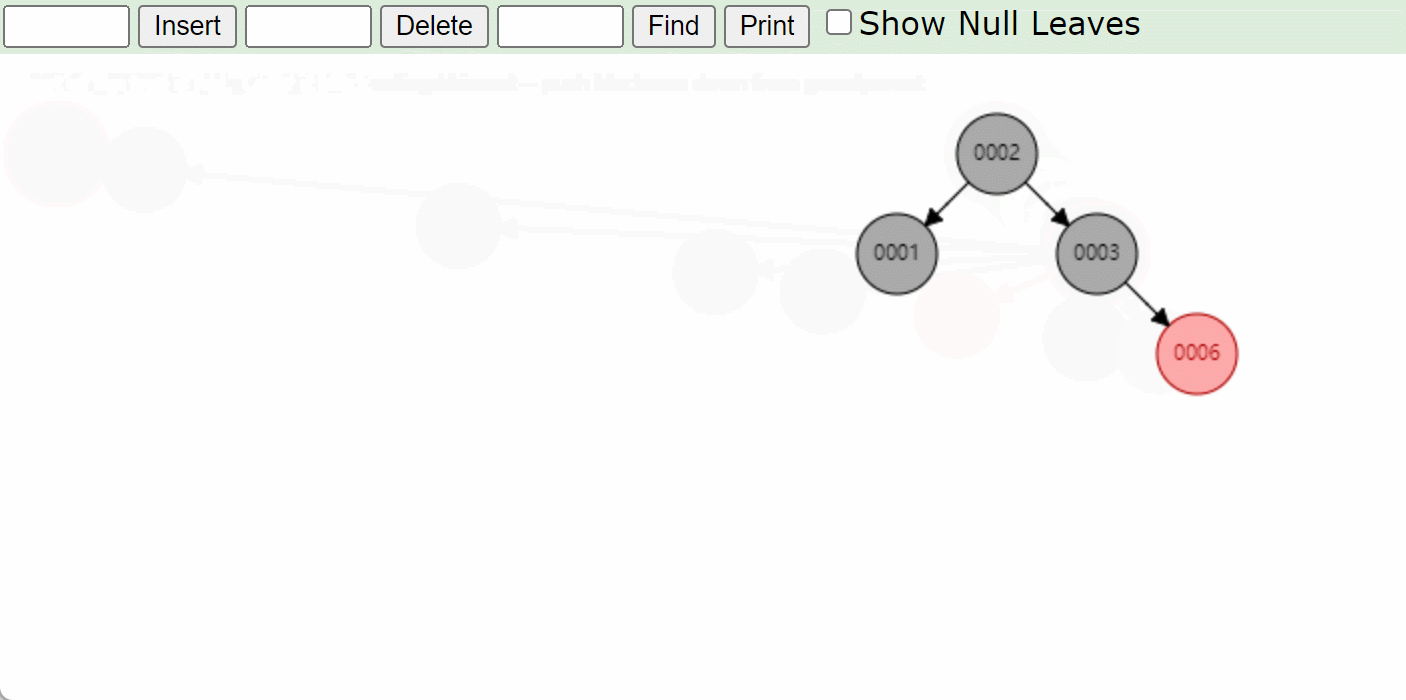
• 右左型RL：先右旋将模型转成右右类型RR，将6这个结点变成新输入的结点然后再左旋然后变色。
  
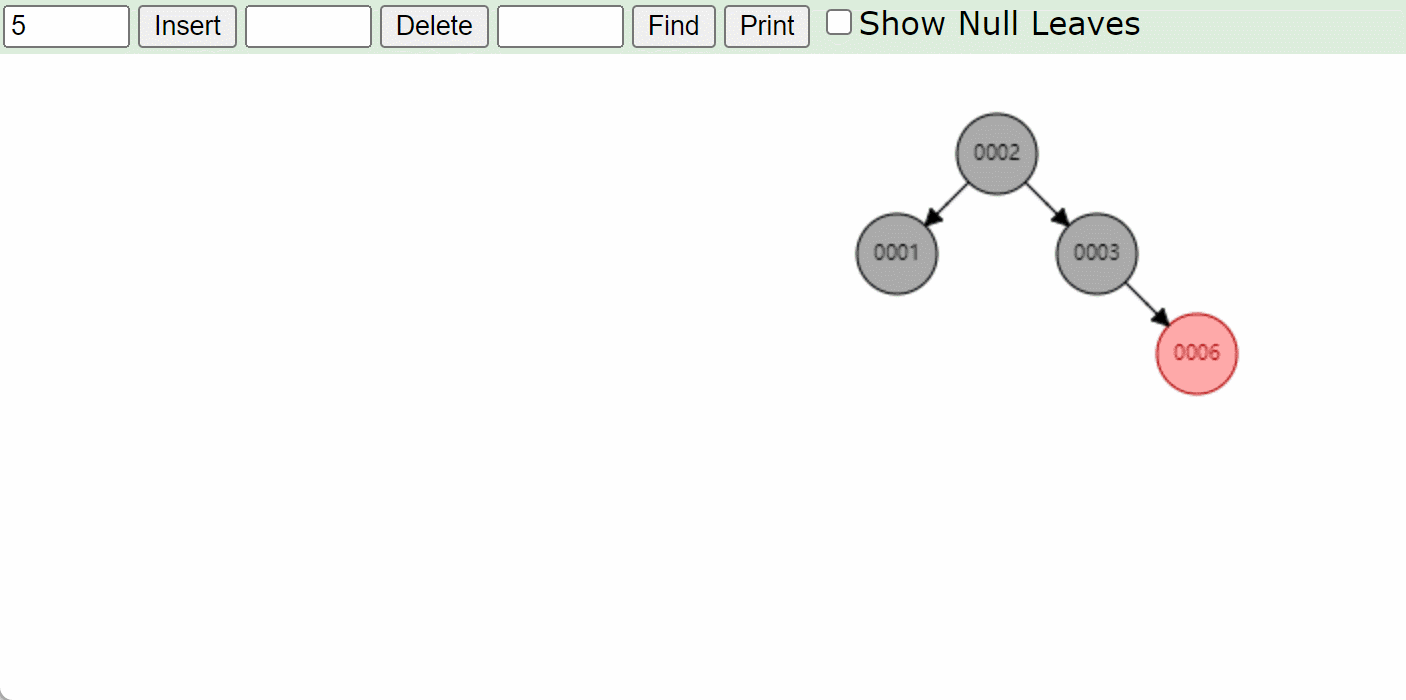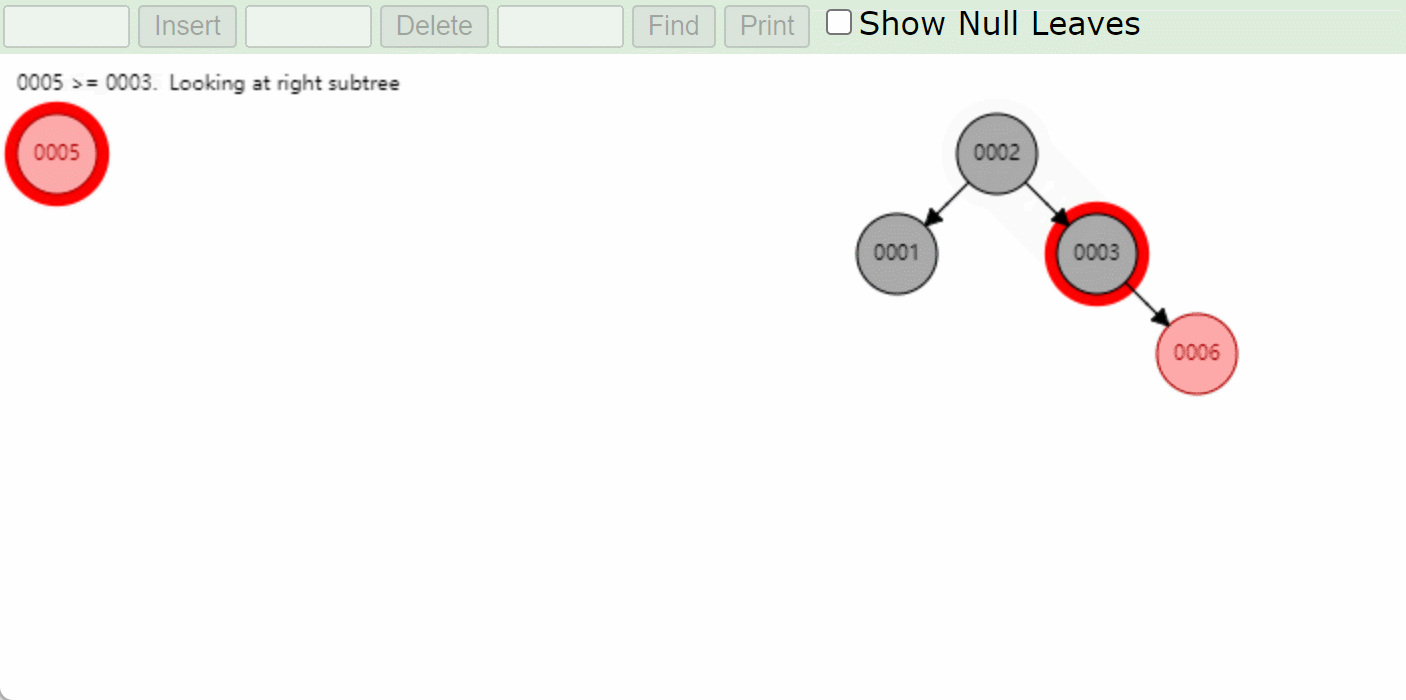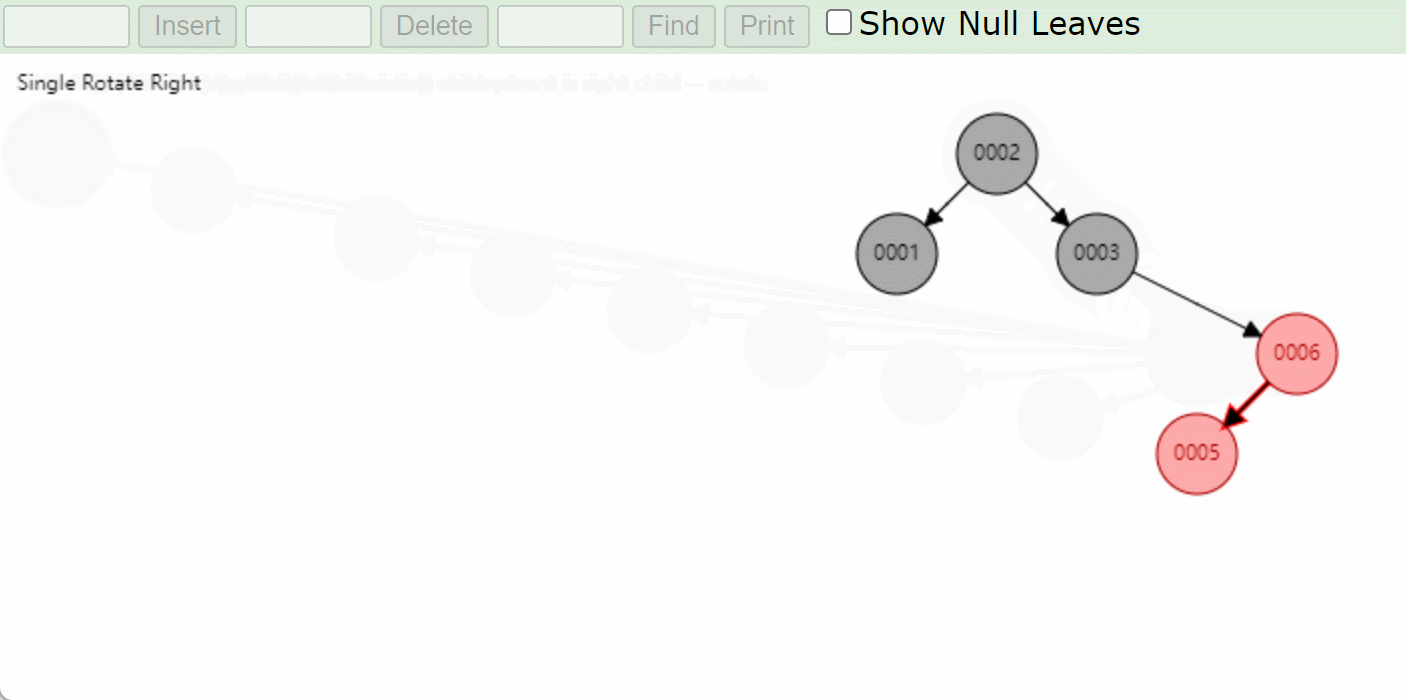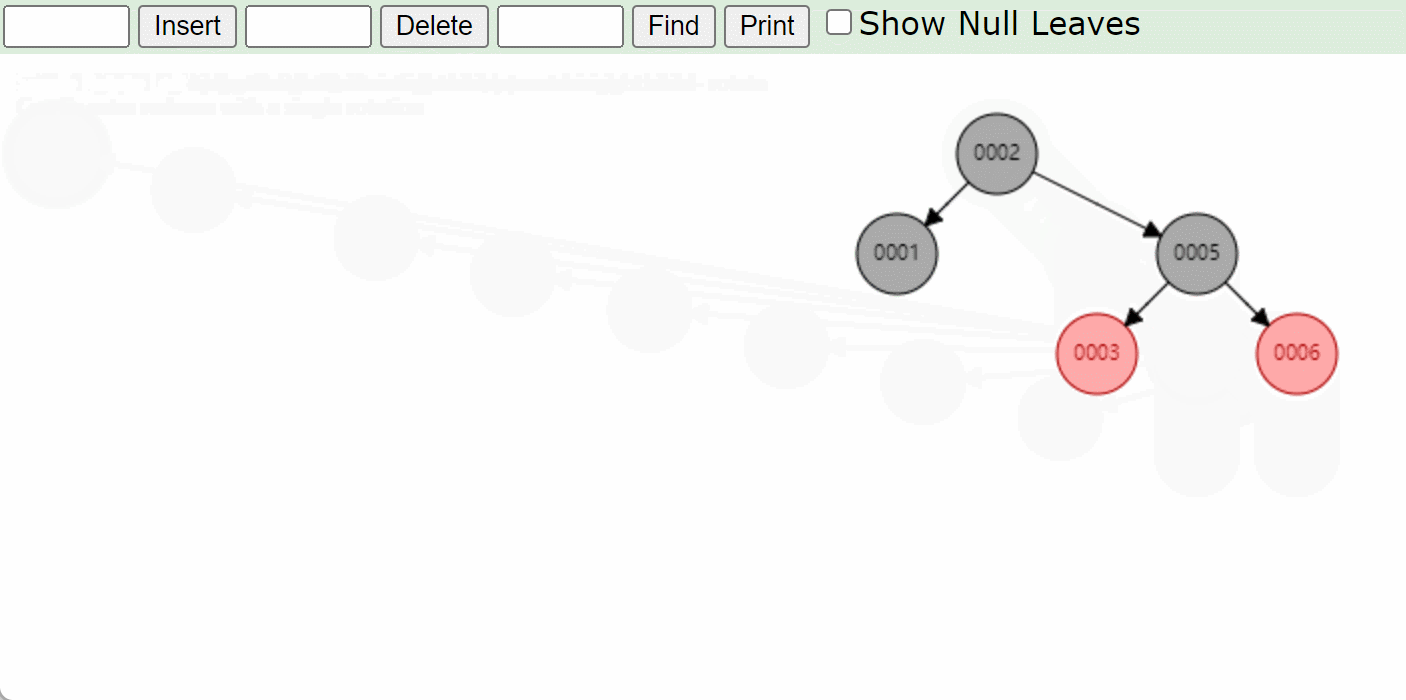
  注意：左左和左右型都是和上面的基本上是一样的知识变换了一下位置而已所以这里就不在赘述了！

最后

最后一点需要说明的时候红黑树是很重要的一个知识点，在大厂的面试中特别喜欢问红黑树相关的知识点，尤其是他是如何自平衡的和AVL树的自平衡有什么区别！！
好了，红黑树的自平衡整理的差不多收工！

彩蛋

如果说看着我这个动图还是不了解的同学，给你们推荐一个网站，可以自己动手去实现！这样更快上手！希望对你的理解有更大的帮助！
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html