[数据结构与算法][CQOI2014] 危桥（网络流）

problem

luogu-P3163

solution

这是一道网络流好题，看的着摸不着吃不着。

初读完题，就知道这是一道“脱光了”的最大流。

建图基础版本：

• 建立额外源汇点。

• 无向边相同于两条有向边，直接建不影响，危桥流量设成 $2$ ，否则 $\infty$ 即可。

• $s\to a_1$ 流量 $a_n?2$，$s\to b_1$ 流量 $b_n?2$，$a_2\to t$ 流量 $a_n?2$ ，$b_2\to t$ 流量 $b_n?2$。

  网络流不能跑环流，所以一次往返我们就拆成两次单向的，反正边也是无向边。

然后 通过样例？ 其实建完就会觉得有点不对劲。因为我们很容易想到其实危桥会被走 $4$ 次。但是又不能将两条有向边的流量变成 $1$，因为万一需要从同一个方向走两边呢？
所以我们想到了类比拆点。

进阶建图版本：

• 建立源汇点。
• 无向边仍看作两条有向边。
• 危桥边，拆成 $x,x+1$，然后 $u,v\to x$ 流量无穷，$x\to x+1$ 流量为 $2$，$x+1\to u,v$ 流量无穷。
• $s\to a_1$ 流量 $a_n?2$，$s\to b_1$ 流量 $b_n?2$，$a_2\to t$ 流量 $a_n?2$ ，$b_2\to t$ 流量 $b_n?2$。

咦~~成功过了样例。一跑大样例，直接寄寄，全是 yes。然后就随便找了一个小的。

4 0 2 1 3 1 1
XOXX
OXNX
XNXO
XXOX

输出中间数据，我惊奇发现路径是从 $a_1$ 到 $b_2$ 的。完全不是一个东西！！

这就是初中语文老师说的，这个政策的投票是否有没有取得压倒性优势，你凭什么让是一定和有配对，凭什么不能是和没有配对？

然后我就想到先只让 $a_1,a_2$ 跑一遍，然后再残余网络上再跑一遍 $b_1,b_2$ 。还是没过，啊~我傻了，第二遍不还是调整了第一遍的流量路径，拆不拆开根本不影响。

我就陷入了无尽的沉思。。。。。。

我不断画图，得出其实无非就是出现了如图的路径不匹配：
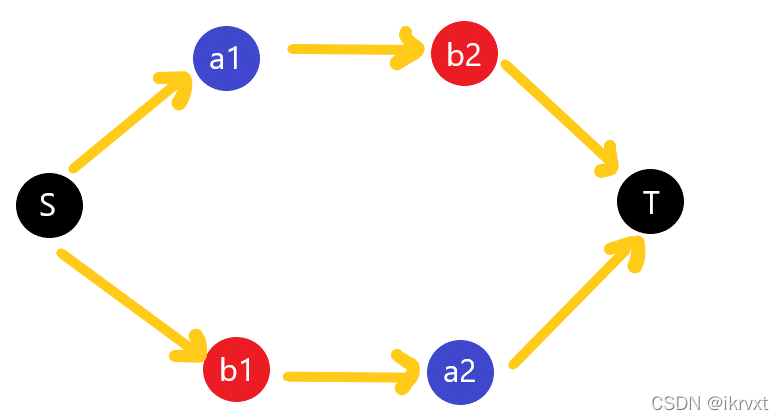两人像是用了魔法门互相传送在走。

很妙的做法是 第一遍不变跑一次，第二遍将 $a_1,a_2$ 换一下，变成从 $a_2$ 到 $a_1$，当且仅当两遍的最大流均为 $a_n+b_n$ 时才为 $yes$ 。

终极建图版本：

• 建立源汇点。
• 无向边仍看作两条有向边，流量无穷。
• 危桥仍看作两条有向边，流量均为 $1$。
• 第一遍 $s{\to }^{a_n}{a}_1,s{\to }^{b_n}{b}_1,a_2{\to }^{a_n}t,b_2{\to }^{b_n}t$。
  第二遍交换 $a_1,a_2$ 其余不变。

之所以这样是正确的前提就是这个边是无向边，所以如果真的是有解的话，我的起终点地位就是等价的，是可以互换的。

别把 $a_1,a_2,b_1,b_2$ 同时换了，负负得正，等于白换。

我只是在进阶版本拆开反思部分，恰好写错了，然后肉眼查出来就改了，改了过不了我就突然想起这个写错的部分，想着试一下，欸他过了

code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define mod 12345678
int n, m, ans;
int px[10], py[10];
char ch[10][10];
int vis[10][10];
int f[1 << 10][30];

bool inside( int x, int y ) {
    if( x < 0 or x >= n or y < 0 or y >= m ) return 0;
    else return 1;
}

int calc() {
    memset( f, 0, sizeof( f ) );
    int tot = 0;
    for( int i = 0;i < n;i ++ )
    for( int j = 0;j < m;j ++ )
        if( ch[i][j] == 'X')
            px[tot] = i, py[tot] = j, ++ tot;
    f[0][0] = 1;
    for( int s = 0;s < (1 << tot);s ++ ) {
        memset( vis, 0, sizeof( vis ) );
        for( int i = 0;i < tot;i ++ )
            if( ! (s >> i & 1) )
                for( int x = -1;x <= 1;x ++ )
                for( int y = -1;y <= 1;y ++ )
                    if( inside( px[i] + x, py[i] +  y) )
                        vis[px[i] + x][py[i] + y] = 1;
        int cnt = n * m;
        for( int i = 0;i < n;i ++ )
        for( int j = 0;j < m;j ++ )
            cnt -= vis[i][j];
        for( int i = 0;i <= cnt;i ++ )
            if( f[s][i] ) {
                ( f[s][i + 1] += f[s][i] * ( cnt - i ) ) %= mod;
                for( int j = 0;j < tot;j ++ )
                    if( ! (s >> j & 1) )
                        ( f[s | (1 << j)][i + 1] += f[s][i] ) %= mod;
            }
    }
    return f[(1 << tot) - 1][n * m];
}

void dfs( int x, int y, int k ) {
    if( x >= n ) return ( ans += k * calc() ) %= mod, void();
    if( y >= m ) dfs( x + 1, 0, k );
    else {
        dfs( x, y + 1, k );
        bool flag = 1;
        for( int i = -1;i <= 1;i ++ )
        for( int j = -1;j <= 1;j ++ )
            if( inside( x + i, y + j ) and ch[x + i][y + j] == 'X' )
                flag = 0;
        if( flag ) {
            ch[x][y] = 'X';
            dfs( x, y + 1, -k );
            ch[x][y] = '.';
        }
    }
}

signed main() {
    scanf( "%lld %lld", &n, &m );
    for( int i = 0;i < n;i ++ )
        scanf( "%s", ch[i] );
    for( int i = 0;i < n;i ++ )
    for( int j = 0;j < m;j ++ )
        if( ch[i][j] == 'X' ) 
            for( int x = -1;x <= 1;x ++ )
            for( int y = -1;y <= 1;y ++ )
                if( ( x or y ) and inside( i + x, j + y ) and ch[i + x][j + y] == 'X' )
                    return puts("0"), 0;
    dfs( 0, 0, 1 );
    printf( "%lld\n", ( ans + mod ) % mod );
    return 0;
}