[数据结构与算法] 蓝桥杯学习记录||ALGO-996 车的放置

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 蓝桥杯学习记录||ALGO-996 车的放置 -> 正文阅读

[数据结构与算法]蓝桥杯学习记录||ALGO-996 车的放置

车的放置

问题描述
　在一个n*n的棋盘中，每个格子中至多放置一个车，且要保证任何两个车都不能相互攻击，有多少中放法(车与车之间是没有差别的)
输入格式

包含一个正整数n

输出格式

一个整数，表示放置车的方法数

样例输入

2

样例输出

7

数据规模和约定

n<=8【样例解释】一个车都不放为1种，放置一个车有4种，放置2个车有2种。

解析：从样例可以看出‘车’是被放在格子里面的，而不是点上。我们可以自由选择摆放车的个数，以达到最多的摆法。

解法：其实可以用概率论的方法解题
当棋盘为n * n 时，我们可以选择的棋子数为0 ~ n ,
　棋子数为0 这算一种
　棋子数为i 可以摆法的种数：
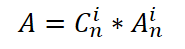
在这里插入图片描述
在n行格子中选择i行进行摆放就是C(i,n)
然后在摆放i个棋子时，第一个棋子有n种选择（n个列可以选），第二个有n-1种选择…就是A(i,n)

写代码时公式可以化简为下图；cal（）就是A的计算函数
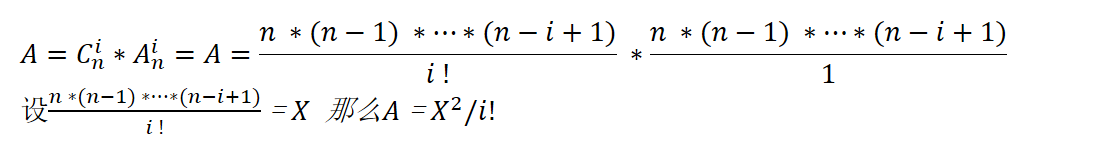
在这里插入图片描述

#include<stdio.h>
int n;
int sum = 0;
//看上图
int cal(int x){
	int factor=1,i;
	for(i=n;i>n-x;i--){ //求分子
		factor*=i;
	}
	factor *= factor; //分子平方
	for(i=x;i>=1;i--){ //除于i的阶层
		factor/=i;
	}
	return factor; //求出A
} 
 
int main(){
	int i;
	scanf("%d",&n);
	sum=1 + n*n; //先把摆放0个和摆放1个的加上
	for(i=2;i<=n;i++){
		sum+=cal(i);//表示用 i 个车 
	}
	printf("%d",sum);
	return 0;
}