[数据结构与算法]平衡二叉树的c++实现

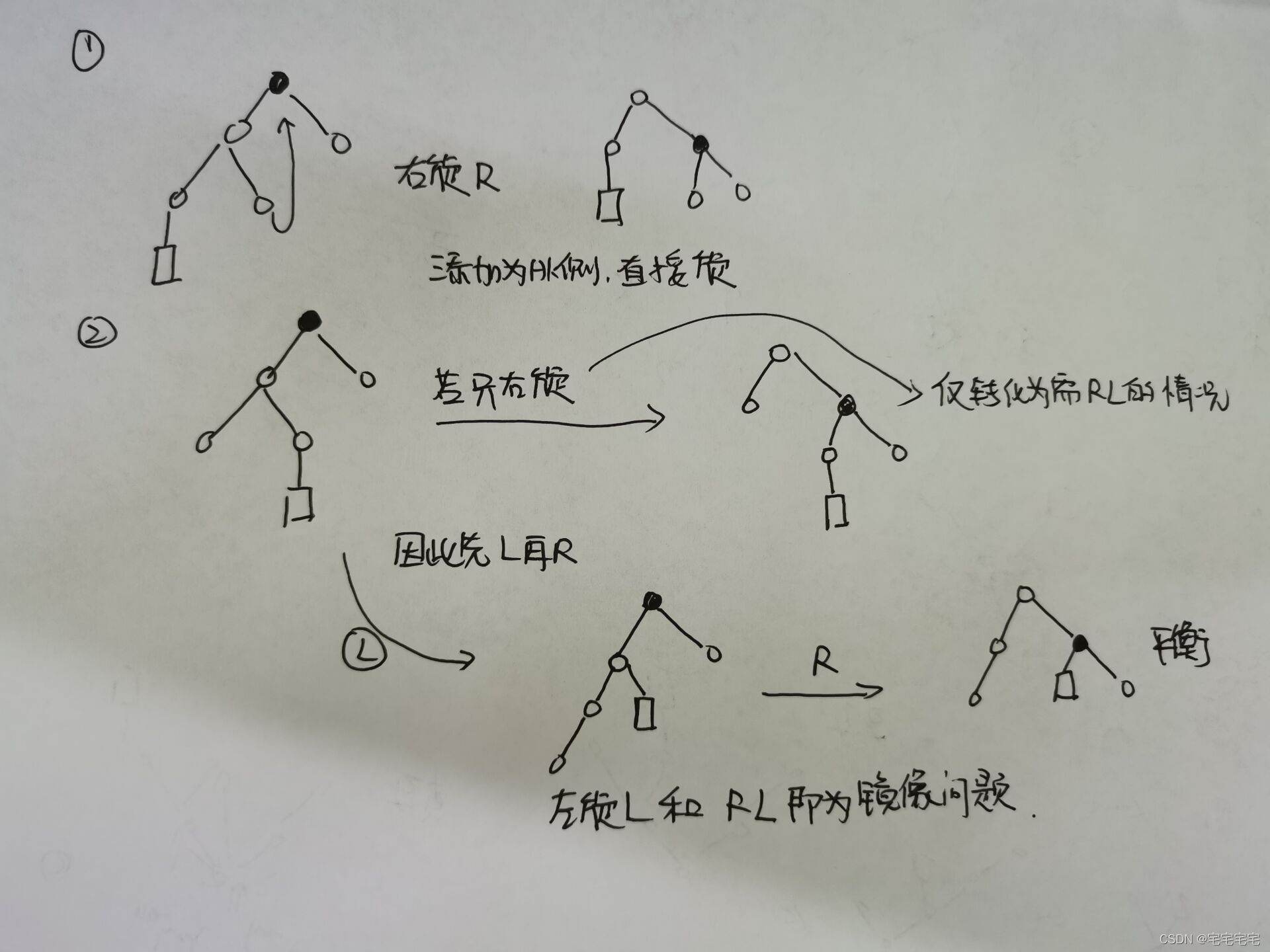
插入节点：
(为什么可以将其移动到另一方作为子树，考虑其左小于父节点以及右大于父节点的性质，即可理解可移动)

二叉树删除节点：
1.若删除节点为叶子节点==》直接删除
2.欲删除节点只有一个子树，删除该head,把子树移到head位置
3.欲删除节点有双子树，（右子树的最左节点为大于且最接近欲删除节点的值）找到该最接近节点node将其与欲删除节点交换，问题转换为{
删除右子树中，值为node->key的节点（该节点为叶子节点或只有右子树的节点）<即转换为1，2情况>
}

AVLTree.hpp

#pragma once
#include <iostream>
using namespace std;

template <typename T>
struct Node
{
    T key;
    int height;
    Node *left, *right;
    Node(T x)
    {
        key = x;
        height = 1;
        left = nullptr, right = nullptr;
    }
};

template <typename T>
class AVLTree
{
public:
    AVLTree();
    int getN();
    void insert(T x);
    void remove(T x);
    bool search(T x);
    void inorder();

private:
    int n;
    Node<T> *root;
    int height(Node<T> *head);

    Node<T> *leftRotation(Node<T> *head);
    Node<T> *rightRotation(Node<T> *head);
    Node<T> *insertUtil(Node<T> *head, T &x);
    Node<T> *removeUtil(Node<T> *head, T &x);
    Node<T> *searchUtil(Node<T> *head, T &x);
    void inorderUtil(Node<T> *head);
};

AVLTree.cpp

#pragma onces
#include "AVLTree.hpp"
#include <iostream>
using namespace std;

template <typename T>
AVLTree<T>::AVLTree()
{
    root = nullptr;
}
template <typename T>
void AVLTree<T>::insert(T x)
{
    root = insertUtil(root, x);
}

template <typename T>
void AVLTree<T>::remove(T x)
{
    root = removeUtil(root, x);
}

template <typename T>
bool AVLTree<T>::search(T x)
{
    return searchUtil(root, x) != nullptr;
}

template <typename T>
void AVLTree<T>::inorder()
{
    inorderUtil(root);
    cout << endl;
}

template <typename T>
int AVLTree<T>::height(Node<T> *head)
{
    if (head == nullptr)
        return 0;
    return head->height;
}

template <typename T>
Node<T> *AVLTree<T>::leftRotation(Node<T> *head)
{
    Node<T> *newhead = head->right;
    head->right = newhead->left;
    newhead->left = head;
    head->height = 1 + max(height(head->left), height(head->right));
    newhead->height = 1 + max(height(head->left), height(head->right));
    return newhead;
}
template <typename T>
Node<T> *AVLTree<T>::rightRotation(Node<T> *head)
{
    Node<T> *newhead = head->left;
    head->left = newhead->right;
    newhead->right = head;
    head->height = 1 + max(height(head->left), height(head->right));
    newhead->height = 1 + max(height(head->left), height(head->right));
    return newhead;
}

template <typename T>
Node<T> *AVLTree<T>::insertUtil(Node<T> *head, T &x)
{
    if (head == nullptr)
    {

        Node<T> *tmp = new Node<T>(x);
        return tmp;
    }
    if (x > head->key)
    {
        head->right = insertUtil(head->right, x);
    }
    else
    {
        head->left = insertUtil(head->left, x);
    }
    head->height = 1 + max(height(head->left), height(head->right));
    // adjust balance
    int balance = height(head->left) - height(head->right);
    if (balance > 1)
    {
        if (x > head->left->key)
        { // LR
            head->left = leftRotation(head->left);
            return rightRotation(head);
        }
        else
        { // R
            return rightRotation(head);
        }
    }
    else if (balance < -1)
    {
        if (x > head->right->key)
        { // L
            return leftRotation(head);
        }
        else
        { // RL
            head->right = rightRotation(head->right);
            return leftRotation(head);
        }
    }
    return head;
}

template <typename T>
Node<T> *AVLTree<T>::removeUtil(Node<T> *head, T &x)
{
    if (head == NULL)
        return NULL;
    if (x < head->key)
    {
        head->left = removeUtil(head->left, x);
    }
    else if (x > head->key)
    {
        head->right = removeUtil(head->right, x);
    }
    else
    {
        Node<T> *r = head->right;
        if (head->right == NULL)
        {
            Node<T> *l = head->left;
            delete (head);
            head = l;
        }
        else if (head->left == NULL)
        {
            delete (head);
            head = r;
        }
        else
        {
            while (r->left != NULL)
                r = r->left;
            head->key = r->key;
            head->right = removeUtil(head->right, r->key);
        }
    }
    if (head == NULL)
        return head;
    head->height = 1 + max(height(head->left), height(head->right));
    int bal = height(head->left) - height(head->right);
    if (bal > 1)
    {
        if (height(head->left->left) >= height(head->left->right))
        {
            return rightRotation(head);
        }
        else
        {
            head->left = leftRotation(head->left);
            return rightRotation(head);
        }
    }
    else if (bal < -1)
    {
        if (height(head->right->left) >= height(head->right->right))
        {
            head->right = rightRotation(head->right);
            return leftRotation(head);
        }
        else
        {
            return leftRotation(head);
        }
    }
    return head;
}

template <typename T>
void AVLTree<T>::inorderUtil(Node<T> *head)
{
    if (head == nullptr)
        return;
    inorderUtil(head->left);
    cout << head->key << " ";
    inorderUtil(head->right);
}

template <typename T>
Node<T> *AVLTree<T>::searchUtil(Node<T> *head, T &x)
{
    if (head == nullptr)
        return nullptr;
    if (head->key == x)
        return head;
    if (head->key > x)
        return searchUtil(head->left);
    return searchUtil(head->right);
}

main.cpp

#include "AVLTree.hpp"
#include "AVLTree.cpp"
#include <iostream>
using namespace std;
int main()
{
    AVLTree<float> *t = new AVLTree<float>();
    t->insert(1);
    t->insert(2);
    t->insert(3);
    t->insert(4);
    t->insert(5);
    t->insert(6);
    t->insert(7);
    t->insert(8);
    t->inorder();
    t->remove(7);
    t->inorder();
    return 0;
}

平衡二叉树删除/插入节点需要调整平衡的次数为查找栈O（logn）。
所以需要引入红黑树，每次插入/删除只调整最多两次。
注意每次左旋右旋调整，不平衡父节点都会调动，因此leftRotation和leftRotation都需要返回Node *node新父节点;