[数据结构与算法]【蓝桥杯冲刺 day8】题目全解析 ---附上LeetCode 每日一题

大家好呀，我是秋刀鱼，今天给大家带来的还是蓝桥杯冲刺刷题的题目解析。春色满园关不住，一枝红杏出墙来，不知不觉呢春天气息已经到来，希望大家能够如初春的花朵一样，朝气蓬勃欣欣向荣，也希望大家能每天都有好心情。

??神奇算式

题目传送门

难度：????

知识点：数学模拟

解题思路：

题目给出只需要从 $0?9$ 选出不同的四个数组成一个乘法算式，选数的操作可以使用递归来实现。因为选中的数字不能重复，因此定义数组 used[10] 存放每一个数的选择情况，保证不会有数被重复选中。

当递归选择完四个数后，假设选中的数分别是 1,2,3,4，那么可能的乘法情况分别有：1 *234、12*34、123*4，对于不同的情况需要逐次地判断，判断在代码中的体现是judge()函数，函数依次获取乘号左侧、右侧的数值，并得到相乘后的结果，为了判断相乘后的值由选中的数字组成，可以使用一个set集合存储构成相乘结果的数，再判断每一个选中的数是否在set集合中出现，如果均出现则表明选中的4个数符合题意。

最后别忘了排除掉乘法交换产生的重复情况，也即是让结果值除以二输出。

#include <iostream>
#include <string.h>
#include <set>
using namespace std;
int arr[4];
bool used[10];
int ans = 0;
// 获取arr数组中的值
int getValue(int i, int j) {
    int val = 0;
    for (; i <= j; ++i) {
        val *= 10;
        val += arr[i];
    }
    return val;
}
void judge() {
    for (int i = 0; i < 3; ++i) {
         // 依次获取乘法左右两侧的值
        int left = getValue(0, i);
        int right = getValue(i + 1, 3);
        int value = left * right;
        // set用于去重并判断结果是否符合题意
        set<int>s;
        while (value) {
            s.insert(value % 10);
            value /= 10;
        }
        bool find = true;
        for (int i = 0; i < 4; ++i) {
            if (!s.count(arr[i])) {
                find = false;
            }
        }
        if (find) {
            ++ans;
        }
    }
}
void dfs(int idx) {
    if (idx == 4) {
        judge();
        return;
    }
    for (int i = 0; i < 10; ++i) {
        if (used[i] || (i == 0 && idx == 0)) {
            continue;
        }
        used[i] = true;
        arr[idx] = i;
        dfs(idx + 1);
        used[i] = false;
    }
}
int main()
{
    memset(arr, 0, sizeof(arr));
    memset(used, false, sizeof(used));
    dfs(0);
    // 处理乘法交换次序重复的情况
    cout << ans/2;
    return 0;
}

??缩位求和

题目传送门

难度：????

知识点：字符串与递归

解题思路：

编写递归函数dfs用于执行一次字符串逐位求和。

如果传入的字符串长度为1，直接返回字符串的第一个元素值，注意需要将其转换为int类型。

否则将该字符串逐位相加，并将结果值转为string 类型继续调用dfs函数，实现递归运算。

#include <iostream>
#include <string.h>
#include <string>
using namespace std;

int dfs(string str) {
    if (str.size() == 1) {
        return str[0] - '0';
    }
    int ans = 0;
    for (char c : str) {
        ans += (c - '0');
    }
    return dfs(to_string(ans));
}
int main() {
    string str;
    cin >> str;
    cout << dfs(str);
    return 0;
}

🌀积木大赛

题目传送门

难度：??????

知识点：逻辑分析

题目解析：

题目要求使建造的操作数最小，那么每一次建造都尽可能地去建造更宽的范围。

可以思考，对于任意一段区间上的大厦，假设其最高高度为$MAX$，那么建造这一段的最少操作数是多少呢？**很显然答案是$MAX$，因为不管怎么样我们都需要将木块搭到$MAX$的高度，也就是说最少需要搭$MAX$次。**有了这个前提我们就可以进行接下来的推导。

对于该情况，因为最大值为$MAX$，在铺设$1?MAX$ 块的过程中，通过一层一层铺设，一定能够铺设完剩余的积木块，因此结果是$MAX$，也就是说：对于一段递增到递减的区间内，能够铺设完的最少次数是该区间的最大值。

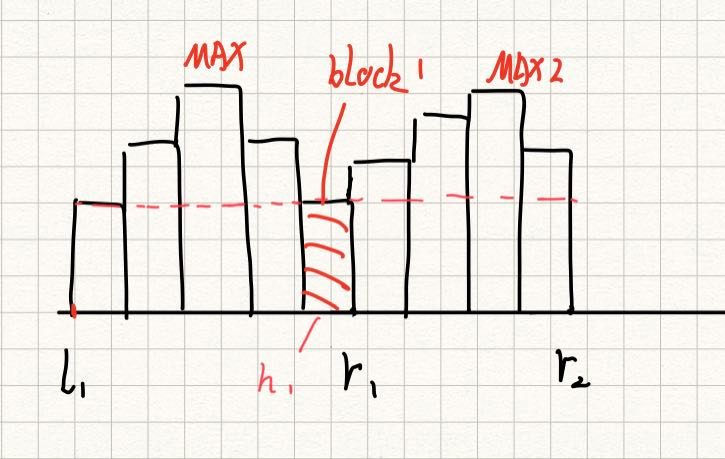
对于上图情况，有多个递增到递减的区间，如果希望铺设的次数最少，我们希望前面的铺设中尽可能大范围地铺设。对于$l_1?r_1$至少需要铺设$MAX$的高度，那么我们希望在这$1?MAX$次铺设中，尽可能帮助区间$r_1?r_2$区间的铺设。那么能够帮助铺设的最大高度，就是两递增递减区间的交界处的高度，也就是图中红色区域高度为 $h_1$ ，对于$r_1?r_2$区间，实际铺设的高度就只有$MAX2?h_1$。

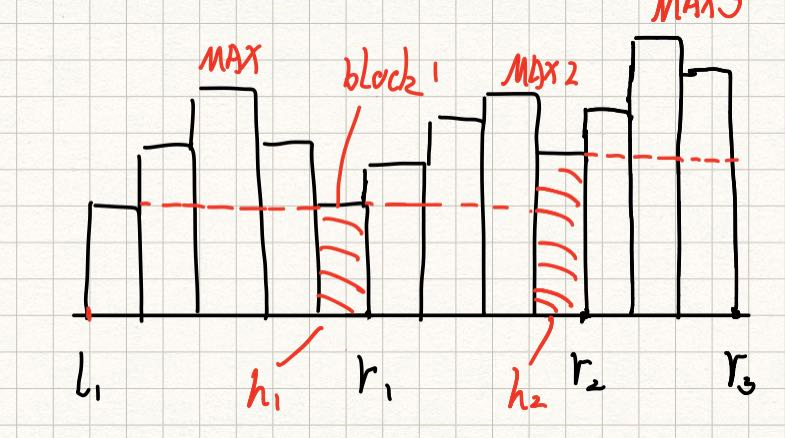
同样对于上面的情况，$r_1?r_2$区间的铺设尽可能多地铺设到$r_2?r_3$区间，在铺设$MAX?MAX2$次时，能够帮助$r_2?r_3$铺设的高度，就是两区间相接部分的高度，也就是$h_2$，实际上铺设$r_2?r_3$的高度为 $MAX3?h2$。

综上所述我们能得到结论：对于每一个递增到递减区间的铺设，假设其最高高度为$MA{X}_i$ ，假设其与前一个递增到递减区间交界方块高度为$h_{i?1}$，那么实际铺设的高度为：$MA{X}_i?h_{i?1}$

于是乎我们可以得到下面的代码：

#include <iostream>
#include <vector>
using namespace std;

int main() {
	int n;
	cin >> n;
	long long ans = 0;
    // 与上一个区间的交界处高度
	int preMin = 0;
    // 上一个方块高度
	int pre = 0;
    // 输入参数，这里在所有方块前放入了一个高度为0的哨兵
	vector<int>query(n+1, 0);
	for (int i = 0; i < n; ++i) {
		int height;
		cin >> height;
		query[i] = height;
	}
    
	for (int i = 0; i <= n; ++i) {
        // 找到了递增到递减区间 开始递减的第一个方块
        // 此时pre 保存的是该递增递减区间的最大高度
		if (query[i] < pre) {
            // 找到交界方块
			while (i < n && query[i] > query[i + 1]  ) {
				++i;
			}
            // 最高高度 - 交界高度
			ans += (long long) pre - preMin;
            // 更新交界高度
			preMin = query[i];
		}
		pre = query[i];
	}
	cout << ans;
	return 0;
}

??LeetCode 每日一题 统计按位或能得到最大值的子集数目

题目传送门

难度：??????

知识点：或操作与位运算

解题思路：

这题的核心点是：某个数组集合的子集合执行或运算的最大值，就是该集合所有元素相或，其实这也是或运算递增性的一种体现。

直接将所有元素相或得到题目要求的最大值，在使用递归遍历所有的子集，将子集或运算结果值与最大值比较，最终得到答案。

class Solution {
    int target = 0;
    int ans = 0;
    public void dfs(int idx,int val,int []nums){ 
        if(idx==nums.length){
            if(val==target){
                ++ans;
            }
            return;
        }
        dfs(idx+1,val|nums[idx],nums);
        dfs(idx+1,val,nums);
    }
    public int countMaxOrSubsets(int[] nums) {
        for(int val:nums){
            target|=val;
        }
        dfs(0,0,nums);
        return ans;
    }
}