目录
链表基础知识
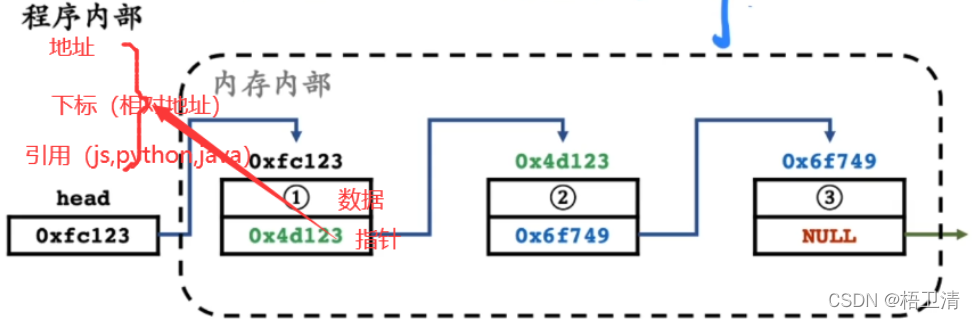
1.链表中的每个节点至少包含两个部分:数据域和指针域;
2.链表中的每个节点,通过指针域的值,形成一个线性结构;
3.复杂度:查找节点O(n),插入节点O(1),删除节点O(1);
4.不适合快速的定位数据,适合动态的插入和删除数据的应用场景。
几种经典的链表实现方法
第1种方法:传统方法
//struct结构体对应了Java或JS中的一个对象,相当于JS中的class,Java中的引用变量
//结构体代表了链表中的一个节点,一个节点中含有数据域和指针域,是链表的结构。
//C语言中的指针相当于Java中的引用
struct Node {
//Node的构造函数,构造Node类的对象的时候,传入一个int类型的data数据。data为当前链表节点存储的值。
Node(int data): data(data),next(NULL){}
int data; //节点数据域,整型;
Node *next; //节点指针域,指向下一个地址
};
int main(){
Node *head = NULL; //头结点
head = new Node(1); //head指向下一个节点
head->next = new Node(2); // head下一个节点的下一个节点
head->next->next = new Node(3);
head->next->next->next = new Node(4); //构建了一条四个节点的链表:1->2->3->4->
//遍历链表,从头开始
Node *p = head;
while(p != NULL) { //当指针p所指的链表不为空时,依次往后遍历
printf("%d->", p->data);
p = p->next;
}
printf("\n");
return 0;
}//第2种方式:
//将链表拆成两个数组,一个装数据域,另一个装指针域
int data[10]; //数据域
int next[10]; //指针域,存储节点下标,相当于相对地址
//添加节点的函数,在相关节点index后添加指针下标为p、值为val的节点
void add(int ind, int p, int val){
next[ind] = p; //next[ind]指向p
data[p] = val; //data中存储的值是val
return ;
}
int main(){
int head = 3; //头结点为3
data[3] = 0; //3节点中存储的是0
add(3, 5, 1); //在3节点后添加指针下标为5、值为1的节点
add(5, 2, 2); //在5节点后添加指针下标为2、值为2的节点
add(2, 7, 3);
add(7, 9, 100); //以上代码构建了一个链表
int p = head; //遍历链表
while (p !=0) {
printf("%d->", data[p]);
p = next[p];
}
printf("\n");
return 0;
}//第2种方式。
//实现可以从链表中间插入节点
//将链表拆成两个数组,一个装数据域,另一个装指针域
int data[10]; //数据域
int next[10]; //指针域,存储节点下标,相当于相对地址
//添加节点的函数,在相关节点index后添加指针下标为p、值为val的节点
void add(int ind, int p, int val){
next[p] = next[ind]; //添加此句使得可以从中间插入节点
next[ind] = p; //next[ind]指向p
data[p] = val; //data中存储的值是val
return ;
}
int main(){
int head = 3; //头结点为3
data[3] = 0; //3节点中存储的是0
add(3, 5, 1); //在3节点后添加指针下标为5、值为1的节点
add(5, 2, 2); //在5节点后添加指针下标为2、值为2的节点
add(2, 7, 3);
add(7, 9, 100); //以上代码构建了一个链表
add(5, 6, 123); //在5和2之间插入节点123
int p = head; //遍历链表
while (p !=0) {
printf("%d->", data[p]);
p = next[p];
}
printf("\n");
return 0;
}经典面试题
LeetCode141环形链表
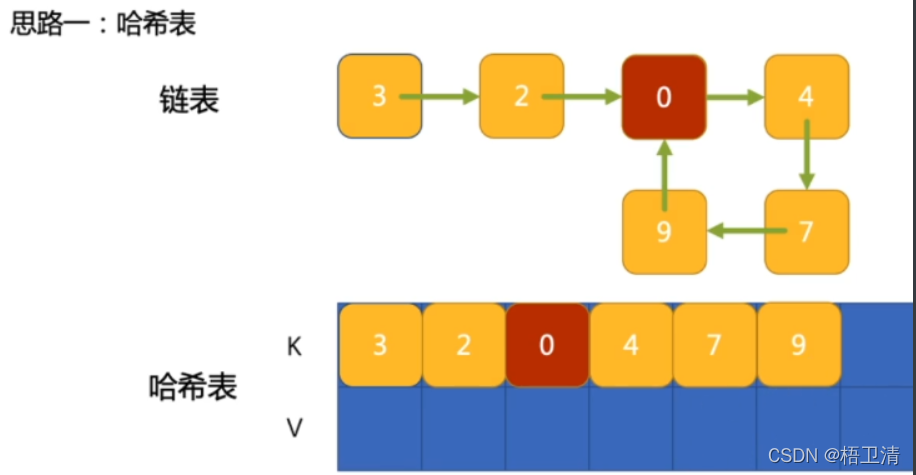
思路1:借助额外存储区
????????依次遍历整个链表,并创建一个哈希表来存储遍历过的节点。在存入哈希表之前,先判断哈希表中是否存在该节点,如果不存在,则存入哈希表。如果已存在,说明遍历到了重复节点,链表有环。如果遍历到next节点为null的节点,说明没有环。
思路2:快慢指针
????????定义两个指针,一个慢指针(用红色标记),一个快指针(用黄色标记),并且,一开始,慢指针指向head节点,快指针指向head.next节点。
????????然后,快指针每次向前移动两步,慢指针每次向前移动一步,进行遍历整个链表。
????????当快指针的next节点为null,或者快指针本身节点为null时,说明该链表没有环,遍历结束。
????????如果链表有环,那么快慢指针一定会相遇,指向同一个节点,当指向同一个节点时,遍历结束。
bool hasCycle(ListNode *head) {
if (head == nullptr) return false; //首先判断,链表是否为空,链表为空则无环
ListNode *p = head, *q = head->next; //定义快慢指针,p慢指针,q快指针
//在p!=q、q和q-next不为空时,p每次走一步,q每次走两步
while (p != q && q && q->next) {
p = p->next;
q = q->next->next;
}
return q && q->next; //如果q不为空节点,说明p,q相遇才退出的循环,说明链表有环
}LeetCode142寻找环形链表起点位置
????????快慢指针相遇后,将其中一个指针放置到起始处,另一个指针放在相遇处,两个指针同时向后移动,每次移动1步,两个指针相遇位置即为环的起点处。根据是,从起始位置到环起点处的距离与环起点处到相遇位置的距离相等。
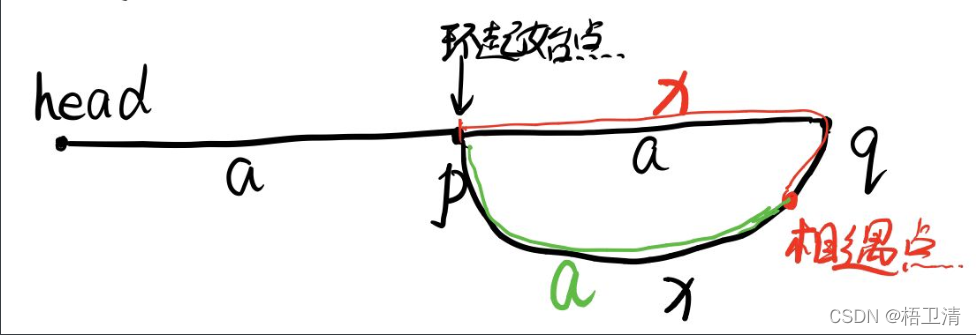
思路分析: ?
(1)假设此时慢指针p位于环起始点,p与head之间的距离为a,即环起始点距离head为a,则此时,q距起始点为2a。
(2)设此时q前行绕环到环起始点距离为x,即快指针q与慢指针p之间距离为x,环的长度为(a+x)。因此,p与q消除完x的距离差之后将会相遇,即p往前走x,q往前走2x,二者将会相遇,此时,相遇点与环起始点的距离(p->q方向)为x,(q->p方向)为a,因为之前已经得知环的长度为(a+x)。
(3)最后可知,head到环起始点与相遇点到环起始点距离相等,这里都等于a。
ListNode *detectCycle(ListNode *head) {
if(head == nullptr) return nullptr; //首先判断链表是否为空,为空则没有环,返回空地址
ListNode *p = head, *q = head->next; //p为慢指针,指向头结点;q为快指针,指向头结点的下一个节点
//首先判断是否有环
//当p != q,q和q->next都不为空时,p每次往后走1步,q往后走两步
while (p != q && q && q->next) {
p = p->next;
q = q->next->next;
}
if(q == nullptr || q->next == nullptr) return nullptr; //当q或q->next为空时,说明没环,返回空地址
//如果执行完以上代码后,未返回,说明链表有环
p = head->next; //将p、q重新放位置,p、q不能放在同一个起点位置,假设都放在head位置,则while下面的while循环将无法执行。
q = head->next->next; //这里不能写成 p = head; q = head->next;
while(p != q) { //链表有环时,此时只需判断p!=q,当p=q时说明二者相遇了
p = p->next;
q = q->next->next;
}
/*
//以上判断p、q相遇点的代码可以使用do while循环实现
p = q = head;
do {
p = p->next;
q = q->next->next;
} while(p != q)
*/
//执行完上面的while循环说明p和q在相遇点相遇了
p = head; //p、q相遇后,将p放回到head。
while(p != q) { //p、q相遇后,p放回到head,然后让p和q同时向后走,第二次相遇点即为环的起始点
p = p->next;
q = q->next;
}
return q; //此时p、q相遇在环起始点,返回所在位置即为环起始点
}简洁版代码
ListNode *detectCycle(ListNode *head) {
if(head == nullptr) return nullptr; //首先判断链表是否为空,为空则没有环,返回空地址
ListNode *p = head, *q = head; //p为慢指针,q为快指针,都指向头结点
if (q->next == nullptr) return nullptr; //判断是否有环,q->next == nullptr说明只有1个节点,无环返回空地址
//首先判断是否有环
do {
p = p->next;
q = q->next->next;
} while (p != q && q && q->next); //当p != q,q和q->next都不为空时,p每次往后走1步,q往后走两步
if(q == nullptr || q->next == nullptr) return nullptr; //当q或q->next为空时,说明没环,返回空地址
//如果执行完以上代码后,未返回,说明链表有环
p = head; //p、q相遇后,将p放回到head。
while(p != q) { //p、q相遇后,p放回到head,然后让p和q同时向后走,第二次相遇点即为环的起始点
p = p->next;
q = q->next;
}
return q; //此时p、q相遇在环起始点,返回所在位置即为环起始点
}