并查集
简介
并查集是一种简单的用途广泛的集合,是一种树形的数据结构,可以实现较快的元素合并和元素是否在某一集合的判断,应用很多,如求无向图的连通个数,带限制的作业排序,实现kruskar算法求解最小生成树等。
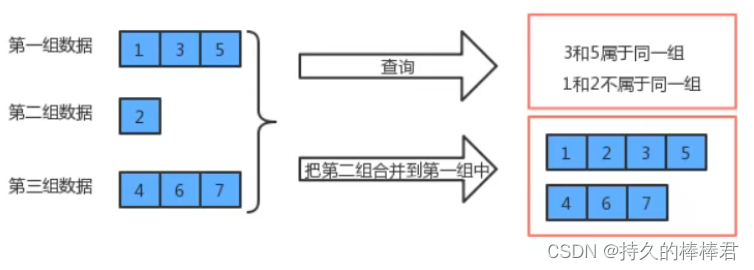
并查集时钟树形结构,但由于二叉树、红黑树、B数不一样,要求比较简单:
1、每一个元素都唯一的对应一个结点
2、每一组数据中的多个元素都在同一棵树中
3、一个组中的数据对应的树和另外一个组中的树之间没有任何联系
4、元素在树中并没有子父级关系的硬性要求
例如:
这是一组,里面有三个元素
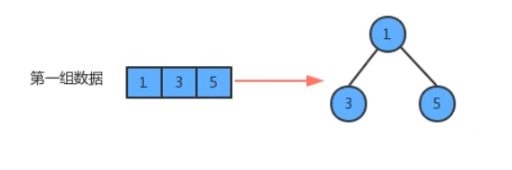
单个元素也可以是一组

因为没有子父级关系,所以可以随便排:
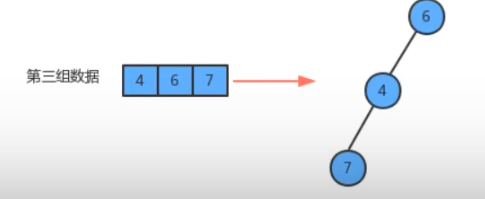
(1)查两个数据是否在同一组可以转换为查看两个数据是否在同一棵树上,而判断两个数据是否在同一棵树上则是判断两个数据结点的根结点是否是同一个
(2)将两个组合并在一起主要是通过将其中一棵树的根结点的指针指向另一棵树的根结点。
主要方法介绍
1、构造方法实现说明:
(1)初始情况下,每个元素都在一个独立的组中,所以在初始情况下,并查集中的数据默认分为N个组(传进N个数据就分成N组)
(2)初始化数组eleAndGroup,把eleAndGroup数组的索引看做是每个结点存储的元素,把eleAndGroup数组每个索引处的值当做索引所在的分组(初始化情况下,i索引处存储的值就是i)
2、union(int p, int q)合并方法实现
(1)如果p和q已经在同一个分组中,则无需合并
(2)如果p和q不再同一个分组,则只需要将p元素所在组的左右的元素的组标识符改为q元素所在组的表示符
(3)每次合并后,分组的数量就会减少一个。
代码实现:
public class UF {
//记录结点元素和该节点所在分组的标识
private int[] eleAndGroup;
//记录并查集中数据的分组个数
private int count;
//初始化并查集
public UF(int N){
//初始化分组的数量,默认情况下有N个分组
this.count = N;
//初始化eleAndGroup数组
this.eleAndGroup = new int[N];
//初始化eleAndGroup中的元素及其所在的组的标识符,
//数组eleAndGroup中的索引作为并查集中每个结点的元素,且让数组每个索引处的值为索引,即eleAndGroup[i]=i;
for (int i = 0; i < eleAndGroup.length; i++) {
eleAndGroup[i] = i;
}
}
//获取并查集中有多少个分组
public int count(){
return count;
}
//元素p所在分组的标识符
public int find(int p){
return eleAndGroup[p];
}
//判断并查集中元素p和元素q是否在同一分组中
public boolean connected(int p, int q){
return find(p) == find(q);
}
//把p元素所在分组和q元素所在分组合并
public void union(int p, int q){
//判断元素q和p是否已经在同一分组中,如果已经在同一分组中,则结束方法
if(connected(p,q)){
return ;
}
//找到p所在分组的标识符
int pGroup = find(p);
//找到q所在分组的标识符
int qGroup = find(q);
//合并后,让p所在组的所有元素的组标识符变为q所在分组的表示符
for (int i = 0; i < eleAndGroup.length; i++) {
if(eleAndGroup[i] == pGroup){
eleAndGroup[i] = qGroup;
}
}
//分组个数减一
this.count--;
}
}
测试代码:
public class UF_test {
public static void main(String[] args) {
UF uf = new UF(5);
//从控制台录入两个要合并的元素,调用union方法进行合并
Scanner sc = new Scanner(System.in);
while(true){
System.out.println("请输入第一个要合并的元素:");
int p = sc.nextInt();
System.out.println("请输入第二个要合并的元素:");
int q = sc.nextInt();
//判断两个元素是否已经在同一组了
if(uf.connected(p,q)){
System.out.println("元素" + p + "和元素" + q + "已经在同一组了");
continue;
}
uf.union(p,q);
System.out.println("当前并查集中还有" + uf.count() + "个分组");
}
}
}
结果:
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
0
当前并查集中还有4个分组
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
2
当前并查集中还有3个分组
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
2
元素1和元素2已经在同一组了
直到最后合并到只剩下一组。。。
算法优化
优化原因:union方法中使用for循环遍历了所有的元素,很明显,合并算法的时间复杂度是O(n^2),当N非常大的时候,它是不合适的。
优化过程:为了提升union算法的性能,需要重新设计find方法和union方法,并且要对eleAndGroup数组的含义重新设定:
1、仍然让eleAndGroup数组的索引作为某个结点的元素;
2、eleAndGroup[i]的值不再标识当前结点所在的分组标识,而是该结点的父结点
find方法优化:
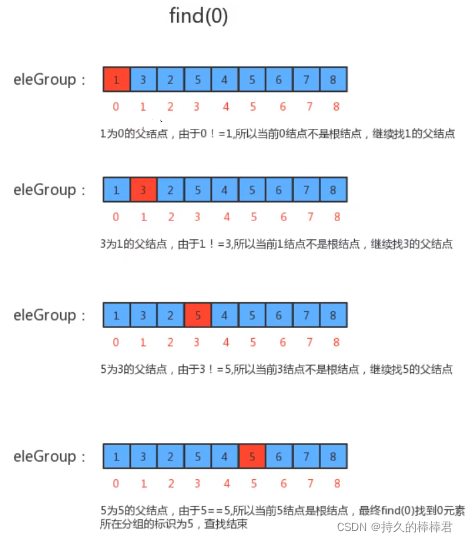
1、判断当前元素p的父结点eleAndGroup[p]是不是索引值,是,则证明自己是根结点了
2、如果当前元素p的父结点不是自己,则让q= eleAndGroup[p],继续找父结点的父结点,直到找到根节点位置。
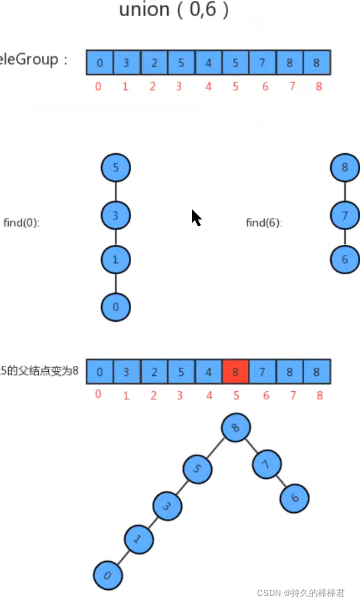
union方法优化
1、找到p元素所在树的根结点
2、找打p元素所在树的根结点
3、如果p和q已经在同一个树中,则无需合并
4、如果p和q不再同一个分组,则只需要将p元素所在树结点的父结点设置为q元素的根结点即可
5、分组数量减一
具体代码
find方法实现:
//找到元素所在分组的根结点
public int find(int p){
while(true){
//判断是不是根结点:根结点的索引和元素值一样(因为初始化数组的时候就是这么定的)
if(p == eleAndGroup[p]){
return p;
}
//这一步意思是:先一步步找到父结点,最后一个父结点即为分组的根结点。
p = eleAndGroup[p];
}
}
union方法实现:
public void union(int p, int q){
//找到p元素和q元素所在组对应的树的根结点
int pRoot = find(p);
int qRoot = find(q);
//判断是不是已经在一组了,是则不需要在进行合并
if(pRoot == qRoot){
return ;
}
//将q所在树的根结点指向p所在树的根结点(即让q的根结点成为p的根结点
eleAndGroup[pRoot] = qRoot;
this.count--;
}
可以发现,优化后的union方法中都没有了for循环,所以时间复杂度变为了O(1)。 但你会发现此时find方法中有添加了一个while(true)循环,而由此可能导致find方法的最坏情况下的时间复杂度是O(N),而所谓的最坏情况就是通过union合并所构成的树成线状,这种树的深度很大,如图:
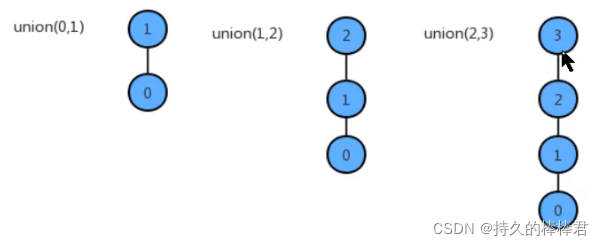
union调用了find方法后,最坏情况下union算法的时间复杂度仍为O(N^2)。这就是所谓的优化了还未完全优化嘛,哎。。。于是,我们要再度优化find方法,使其在遇到这类情况时,使得生成的树的深度尽可能的小,则达到了优化的最终效果。如图:

只要保证每次合并都能把小树合并到大树上,就能够压缩合并后的新树的路径。
最终代码如下:
public class UF_tree_last {
private int eleAndGroup[];
private int count;
private int[] sz; //用来存储每一个根结点对应的树中保存的结点的个数
public UF_tree_last(int N) {
this.count = N; //初始化数组的数量,默认情况系N个分组
this.eleAndGroup = new int[N]; //初始化数组
for (int i = 0; i < eleAndGroup.length; i++) {
this.eleAndGroup[i] = i; //初始化赋值
}
//默认情况下sz中每个索引处的值都是1
this.sz = new int[N];
for (int i = 0; i < sz.length; i++) {
sz[i] = 1;
}
}
public int count(){
return count;
}
//判断两个结点是不是在同一组
public boolean connected(int p, int q){
return find(p) == find(q);
}
//找到元素所在分组的根结点
public int find(int p){
while(true){
//判断是不是根结点:根结点的索引和元素值一样(因为初始化数组的时候就是这么定的)
if(p == eleAndGroup[p]){
return p;
}
//这一步意思是:先一步步找到父结点,最后一个父结点即为分组的根结点。
p = eleAndGroup[p];
}
}
public void union(int p, int q){
//找到p元素和q元素所在组对应的树的根结点
int pRoot = find(p);
int qRoot = find(q);
//判断是不是已经在一组了,是则不需要在进行合并
if(pRoot == qRoot){
return ;
}
// //将q所在树的根结点指向p所在树的根结点(即让q的根结点成为p的根结点
// eleAndGroup[pRoot] = qRoot;
//判断pRoot对应的树大还是qRoot对应的树大,最终需要把较小的树合并到较大的树中
if(sz[pRoot]<sz[qRoot]){
eleAndGroup[pRoot] = qRoot;
sz[qRoot] += sz[pRoot];
}else{
eleAndGroup[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
this.count--;
}
}