[数据结构与算法]堆排序(第二遍分析)

堆排序(第二遍分析)

1.堆排序的算法详解

1.堆排序需要的基础知识

? 1.完全二叉树：完全二叉树是一种特殊的二叉树，它里边的数据排列是要求以先从上到下，再从左到右的顺序进行排列。并且每一层都要从左到右的尽量被铺满，中间不允许出现空位，即使是最后一层铺不满，也要从左到右的尽量铺满。

? 2.大小顶堆：大顶堆指的是在完全二叉树的基础之上，这棵树中的任意一棵子树的根节点都大于或等于其左右孩子的值；小顶堆指的是在完全二叉树的基础之上，这棵树中的任意一棵子树的根节点都小于或等于其左右孩子的值。

2.堆排序算法概述

? 堆排序的整体算法大体上分为两个部分：堆创建部分，排序部分。排序部分又分为两个部分：取值排序部分，取值后的堆维护部分。其中堆维护部分与堆创建部分都用到了一个核心算法：子树根节点放置算法。这个算法名字是我自己取的，所以大家看看就得了，因为根据我的研究分析，发现这个算法的功能为：对于一棵只有两层的树，可以直接将这棵树转变为一个堆；对于两层以上的树，仅能保证将根节点放置在一个让这棵树尽量能符合成堆条件的合适位置上，此时它仅能操作一条路径，如果以该子树根节点的另一个孩子节点为根节点的子树不是堆，那这个算法将无法将这个更小的子树变为堆，关于这个算法，我们在讲完整体的算法流程之后再说，我们先来看看它的算法组成部分图解：

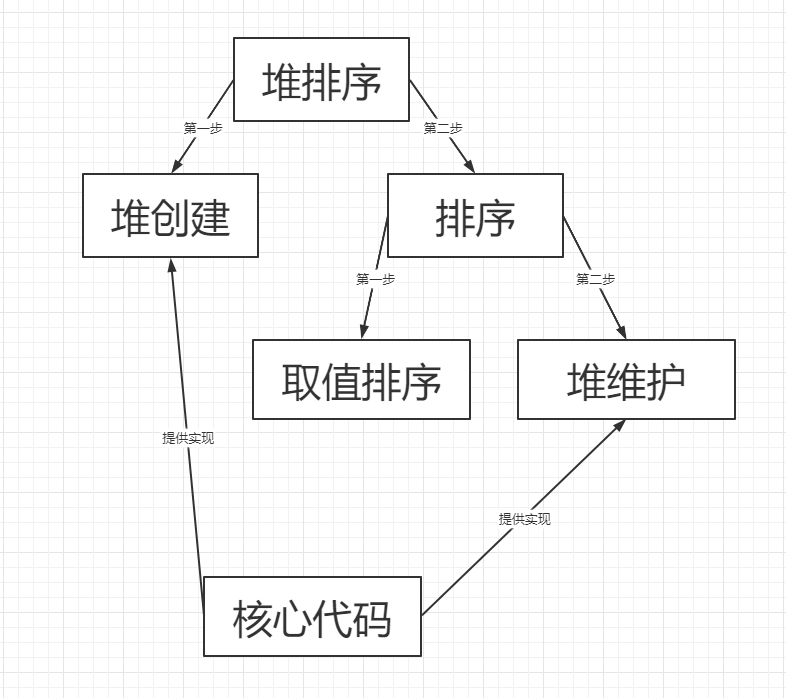
3.堆排序算法图解

? 在此，我们以数组：{1,8,2,5,14,3,7,25,11,6,4}，来进行实例讲解：

1.核心代码

? 我们首先讲解核心代码，这次我们根据已有的代码样例来讲解核心代码：

public static void adjestSort(int[] arr, int parent, int lenght) {//1
        int temp = arr[parent];//2
        int Child = 2 * parent + 1;//3
        while (Child < lenght) {//4
            if (Child + 1 < lenght && arr[Child] < arr[Child + 1]) {//5
                Child++;//6
            }//7
            if (temp >= arr[Child]) {//8
                break;//9
            }//10
            arr[parent] = arr[Child];//11
            parent = Child;//12
            Child = parent * 2 + 1;//13
        }//14
        arr[parent] = temp;//15
    }//16

? 核心代码的参数列表为：数组引用，parent变量，length变量。parent变量是什么？parent变量是一个int类型变量，它的中文意思是：父母，也就是双亲的意思，这里我们取其狭义为：根节点。也就是说parent是一个根节点，那它是怎样的根节点？是这棵树的根节点吗？答案是否定的，继续向下看的话，你会知道它将代表这棵树中某一棵子树的根节点，而在堆创建中，parent将不断的自减，它将依次成为这棵树中每棵子树的根节点，现在我们来看一下，这个核心算法是怎么用的，我们先将一个非常简单的数组{1,4,3,5}带入到里边去：

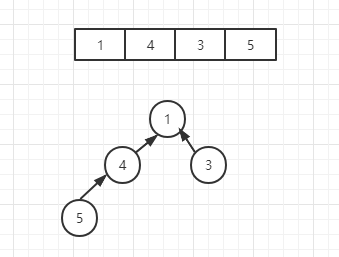
? 在这棵简单的完全二叉树中，我们使用核心算法算一算，我们将数组的首位置也就是树的根节点赋予给parent，数组长度赋予给length，数组引用赋予给arr，我看来看看这个算法会发生什么？

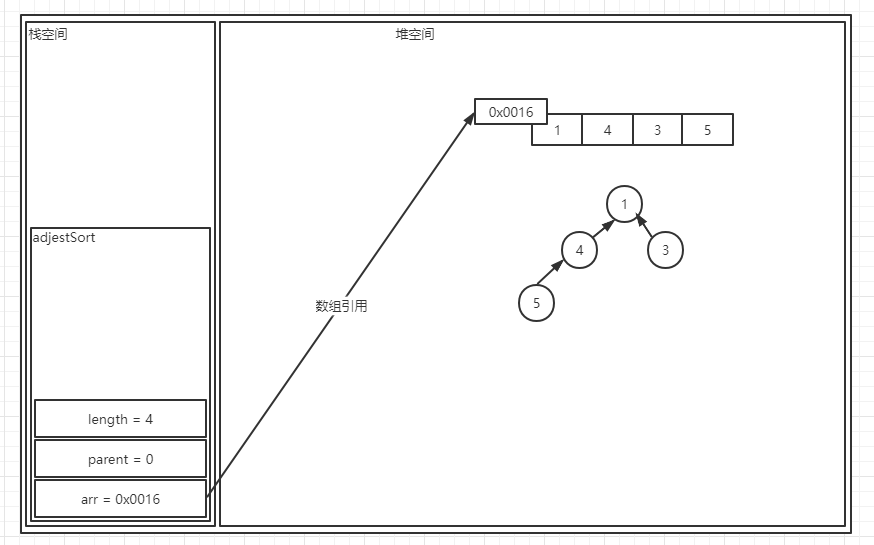
? 在方法刚开始的时候，Java运行时中的部分结构是这样的，之后算法开始执行，在算法运行到第二行第三行时，算法声明了两个变量，temp与Child，temp负责保存parent的值，Child则是指向了根节点左孩子的位置，如图所示：

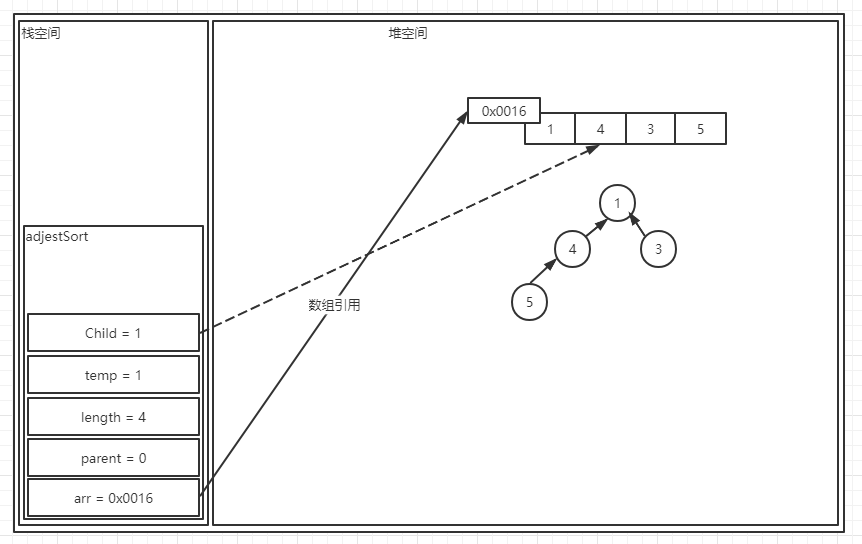
? 之后算法开始运行到第四行，第四行是一个while循环，括号中的条件询问语句的含义是：Child是否小于数组长度？也就是说再问左孩子是否存在？我们知道一个节点在完全二叉树中如果有孩子的话，那肯定是先有左孩子，再有右孩子的，如果没有左孩子那肯定是没右孩子，因此这里实际上是利用了这个规则，查看一下这个节点是否是非叶子节点，如果它有左孩子，那么就肯定是一个非叶子节点，如果连左孩子都没有，那一定是一个叶子结点，我们继续算法：算法现在来到了第五层，第五层是一个if条件语句，其中的询问语句含义比较复杂：Child+1的值是否小于数组长度，并且Child+1位置在数组中所对应的数值是否大于Child位置在数组中所对应的数值。这个语句的含义是在审查完当前节点是否有孩子节点之后，继续审查该节点是否有右孩子节点，如果有右孩子节点，则让其与左孩子节点进行比较，如果右孩子节点比左孩子节点大，那么我们将继续向下进行第六行代码，也就是将Child的数值增大1，孩子节点中和根节点交换的，只有最大的那个，因此如果右孩子节点更大，我们就将这个交换权利给右孩子节点，如果右孩子节点的值不大，那么Child就不变化，参与交换的仍然是左孩子节点。

? 之后我们将进行第八行代码，就是将我们拿到的两个孩子节点中更大的一个与temp也就是根节点的值进行比较，如果temp更大，那么将立即退出程序，因为这时我们将认为这是一个大顶堆，否则的话将要继续向下进行第十一行代码，第十一行代码是将这个孩子节点的值直接赋予给根节点，之后parent的指向发生变化，Child的指向也发生变化，如图：

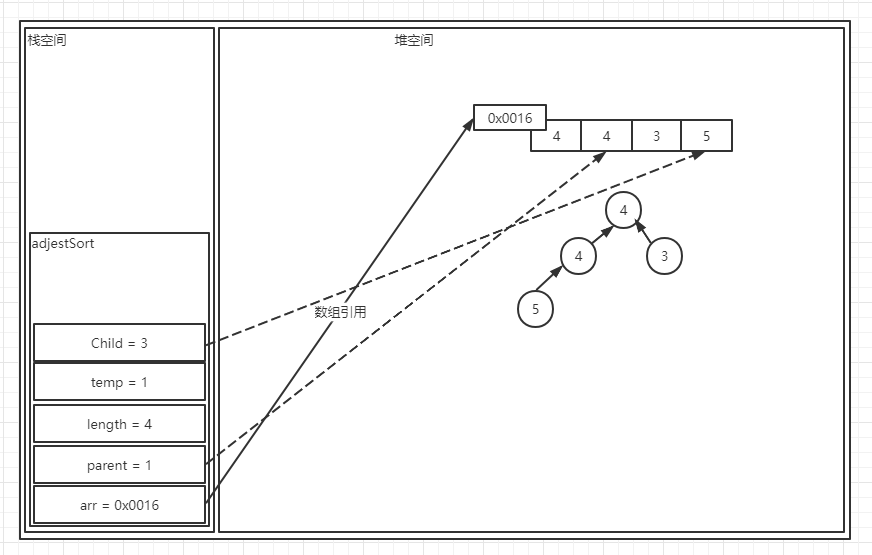
? 我们让parent变量的值变成了Child的值，在此之后我们更新了Child的值，变为了新的parent位置节点的左孩子的值，之后我们重复循环，首先循环条件仍然满足，所以我们继续进行这个比较过程，之后的过程就和上边的过程一样了，首先我们知道这个节点当然仍然是有左孩子，那么我们根据计算看看它有没有右孩子，答案是没有，所以我们只能让左孩子节点和temp进行比较，结果发现左孩子节点仍然是大于当前的temp也就是1的，因此我们直接将左孩子的值给到当前的parent位置上，并更新parent和Child：

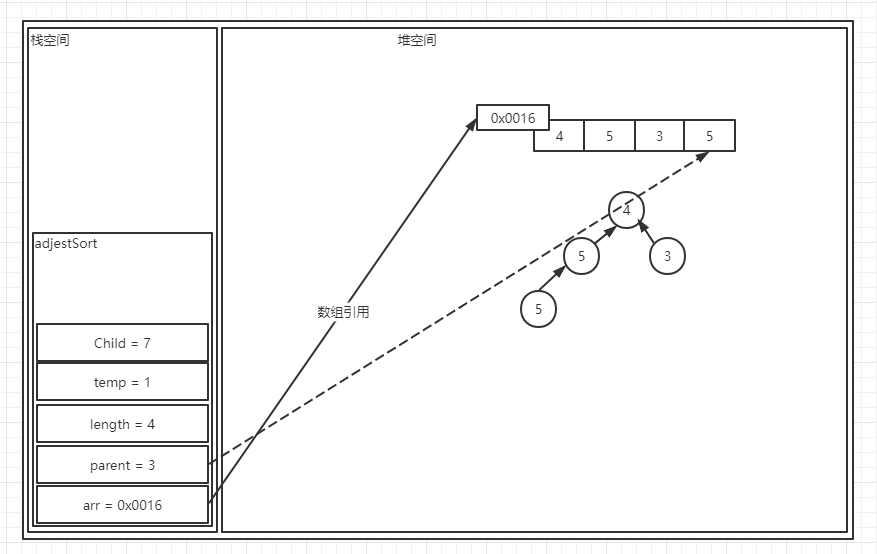
? 可见当前的Child的位置已经是超过length的大小了，因此循环将在下次结束。循环结束后，执行第15行代码，这行代码是将temp赋值给当前parent指向的位置，也就是当前数组中的最后一个位置：

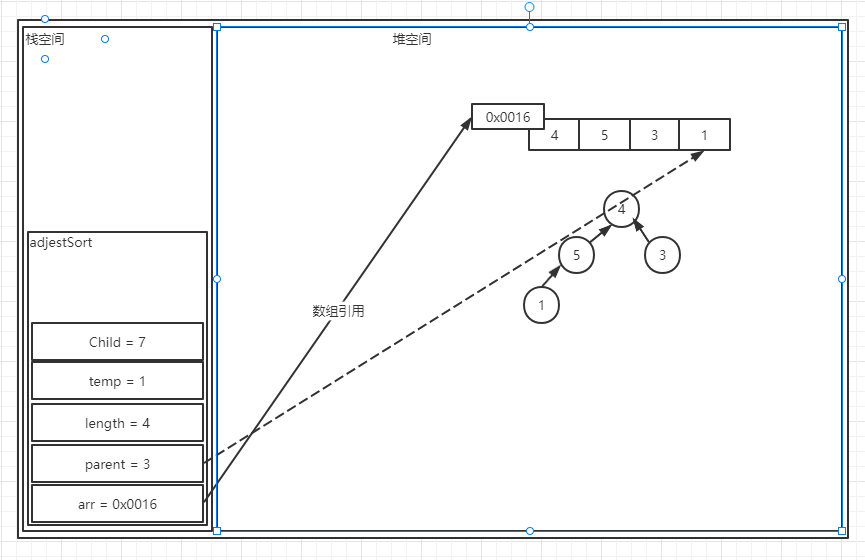
? 至此，一次该算法执行完毕。

? 根据研究该算法的执行，我们可以发现这个算法的基本流程：首先确定得到一个根节点，之后我们获得这个根节点的左孩子，在确定这个左孩子真实存在之后，我们取判断这个节点的右孩子是否存在，如果这个节点的右孩子也存在，那么我们比较两个孩子值的大小，大的将和根节点发生置换，而置换必将伴随着以置换点为根节点的子树可能不再成为堆，因此我们将parent指向发生置换的孩子节点处，继续这个检查与置换的过程，最终到检查到一个位置，这个位置上根节点大于左右孩子节点了，循环停止，这时我们已经确定好了这个算法中最初的根节点应该在的位置，这时我们将它放到这个位置上，算法停止。

? 我们可以发现，这个算法实际上针对的对象是最初的根节点的位置，这个算法运行一次即可以将传入的根节点放入到合适的位置中去，这个算法针对一个深度为二的二叉树可以将该二叉树变为堆，但是无法将深度超过二的二叉树变为堆，因为在这个算法中，参与交换的只有一个孩子节点，在进行这次交换之后会检查以这个孩子节点为根节点的更小的子树是否因为交换而变得不再是一个堆，但是，另一个孩子节点为根节点的子树它没有检查。所以在使用这个算法的时候我们需要保证另一个孩子节点为根节点的子树已经是一个堆了，这样算法才保险。所以这个算法只能是一趟算法，我们需要进行很多趟这个算法，先把底层的比较小的子树变为堆，然后再将上层的比较大的子树变为堆，如果比较小的子树已经是堆了，那么大的子树在进行这个算法的时候，就不必同时在乎两个孩子节点为根节点的子树问题了，所以，这个核心代码需要被套在大顶堆创建代码中。

2.堆创建代码

for (int i = arr.length - 1; i >= 0; i--) {
	adjestSort(arr, i, arr.length);
}

? 堆创建代码就是从后往前不断地调用上面的算法，这样就可以从小到大的来生成堆，并最终创建出一个堆了，接下来我们画图来模拟这个过程。

? 首先我们假设这个算法是运行在一个main函数中的，然后进行了这样的一个循环，循环中我们定义了一个变量i，i一开始的值是arr.length -，在此也就是10，简而言之就是指向了最后一个元素，同时我们是将这个数组看成一棵树的，因此我们在逻辑上是在操控一棵树，所以我们可以画出如下的内存图：

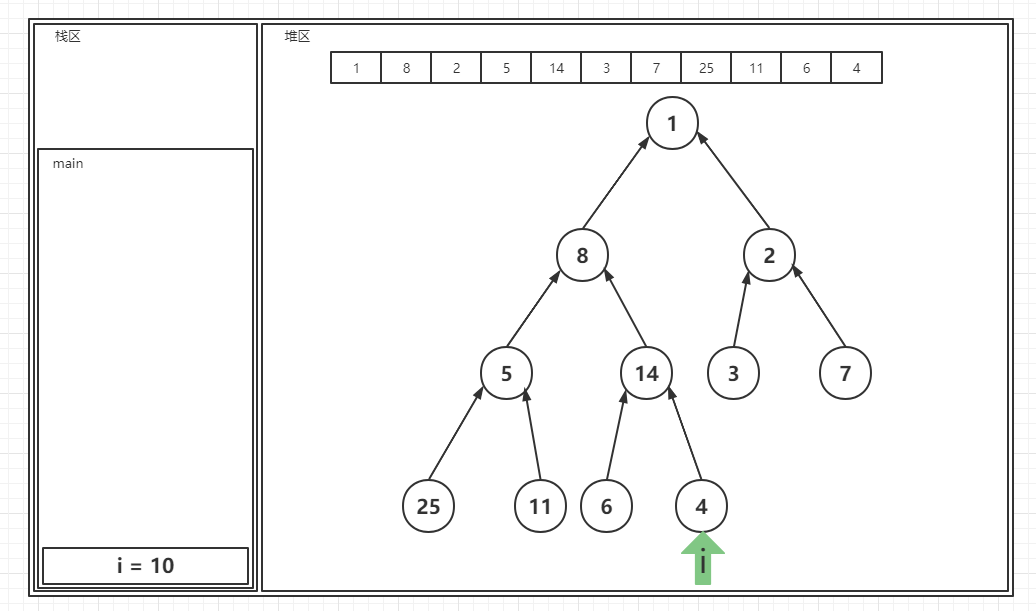
? 可见当前的i指向最后一个元素，图中的树结构是我们想象出来的逻辑结构，并不存在于堆区，存在于堆区的只有数组对象而已。之后我们开始调用核心方法了：在核心方法中，首先会读入i的值，并通过值传递的方式将这个值发送到方法中去：

? 1.

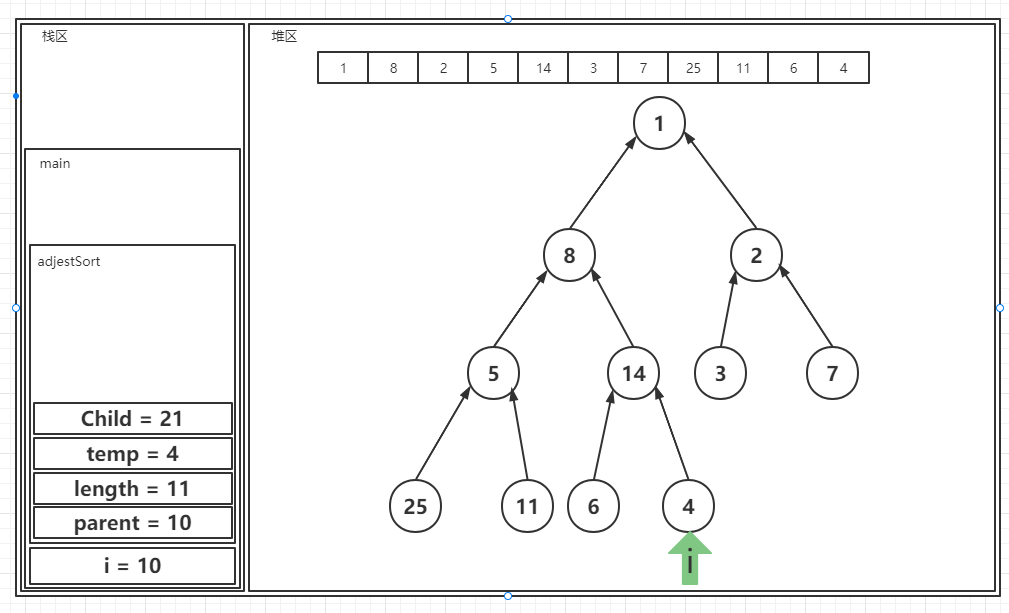
? 新方法入栈之后我们可以得到里边的一些变量的情况：parent指向的位置是10，length的值是11，temp是当前位置的值，而Child的值是21，之后在进行算法的时候，便会因为Child的值大于length的值而终止程序，也就是说当前节点因为仅仅是个叶子结点，所以不予考虑。

? 2.之后程序继续向下进行，i自减一次，指向位置9，如图：

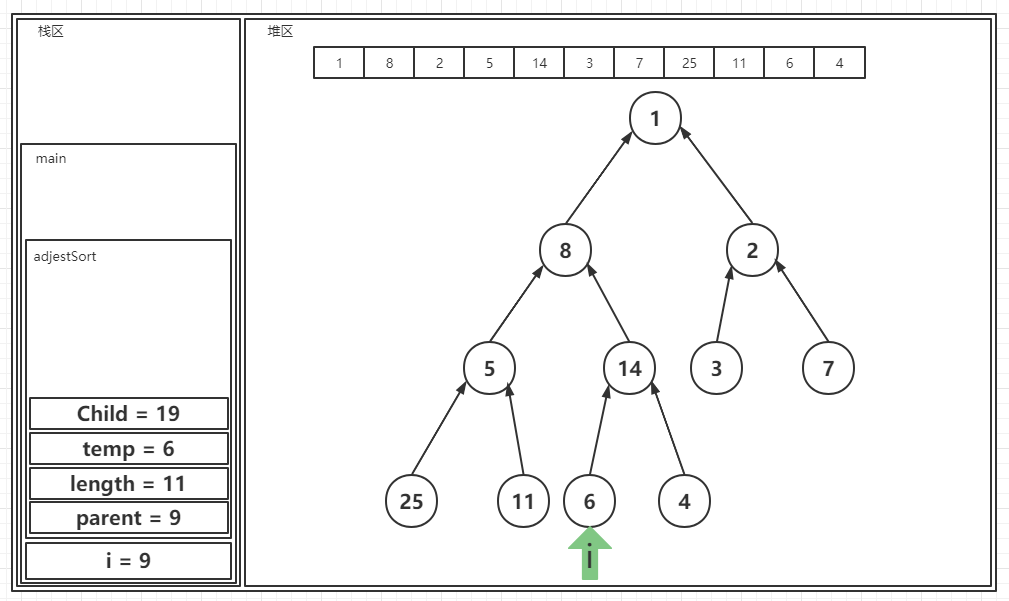
? 3.核心算法仍然不会被触发，因为Child仍然大于length值。继续向下执行：

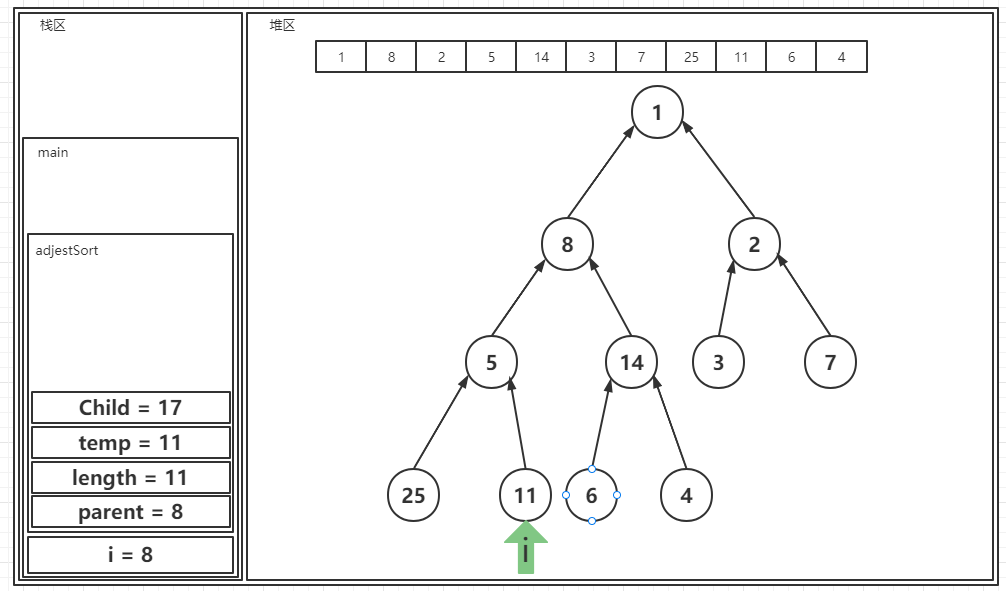
? 4.原因同上，核心方法不会被触发。继续执行：

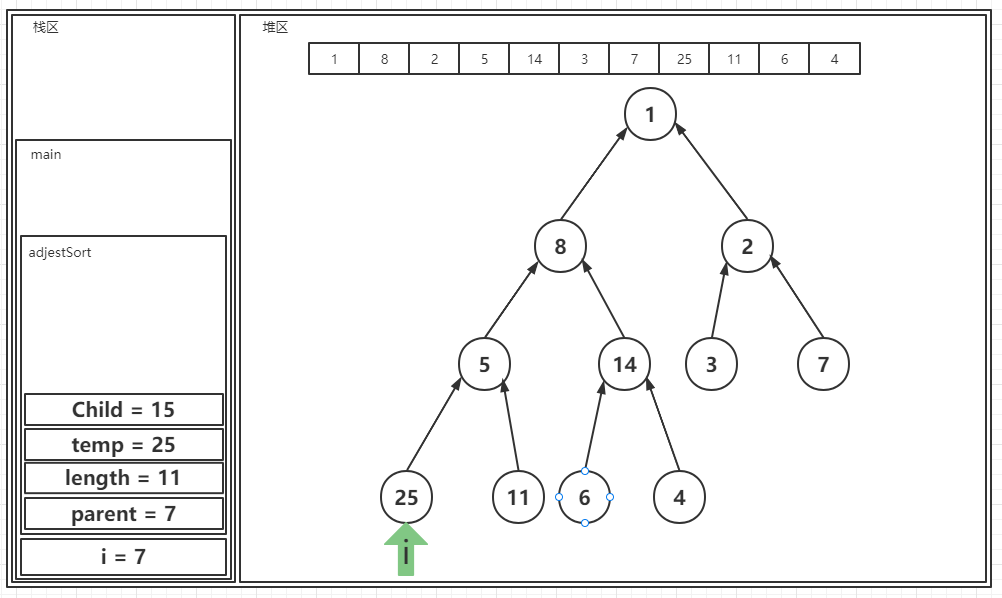
? 5.原因同上，核心方法不会被触发。继续执行：

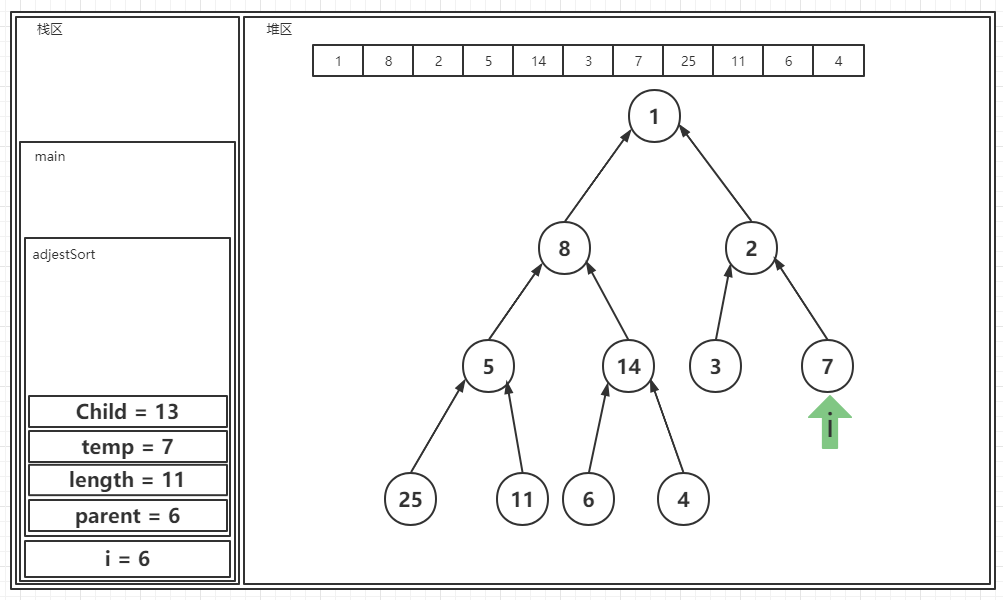
? 6.原因同上，核心方法不会触发，继续执行：

? 7.原因同上，核心方法不会被触发，继续执行：

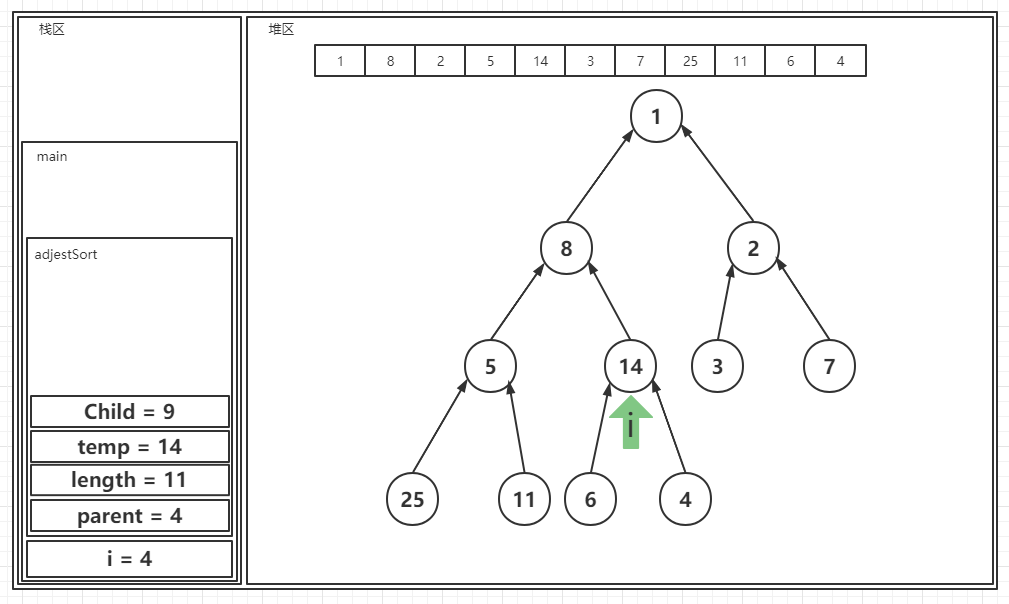
? 转机出现了，在运行到这个状态的时候，Child首次小于length，因此核心方法被触发，开始执行核心方法：首先我们取得Child的值，以此得到Child+1的值也就是10，让10和length对比，看右孩子节点有没有，答案是有，因此进入下一步的左右孩子比大小环节，根据对比是左孩子节点大，所以参与对比的是左孩子节点，Child不自增了。之后我们让temp的值和参与交换的孩子节点的值进行比较，发现temp大于Child位置上的值，所以我们认定这个子树是一个大顶堆，核心方法出栈，继续向下执行：

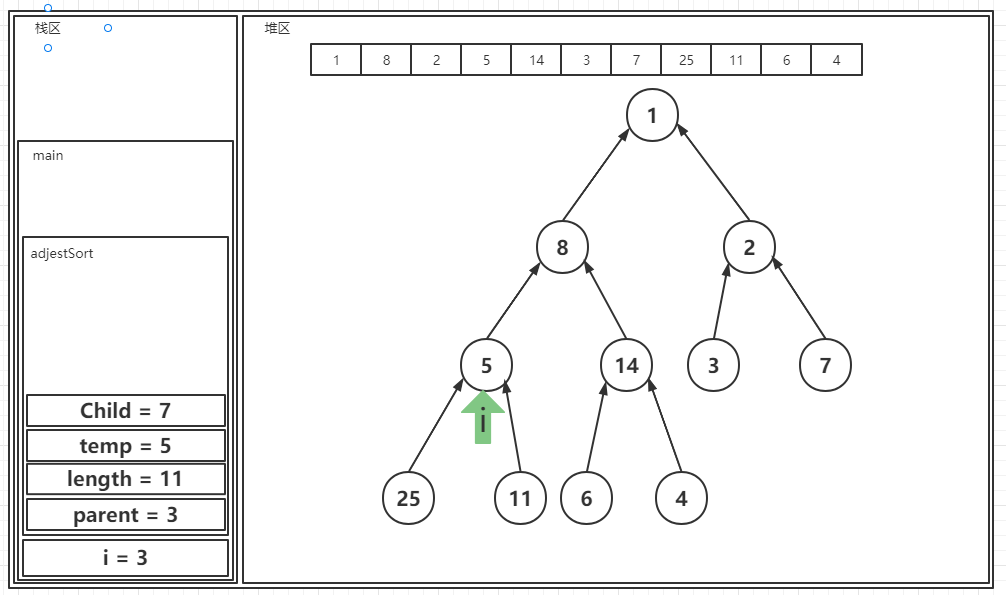
? 8.此时i指向了第四个位置，Child为7,7小于length，因此会触发核心方法，过程为：根据Child的位置来得到Child+1也就是右孩子的位置，然后和右孩子对比，这里的右孩子是11,25大于11因此参与交换的是左孩子，左孩子的值被拿来喝temp比较，发现左孩子的值更大，因此发生一次交换行为，左孩子的值直接被赋予给根节点，并且在此之后，考虑到交换导致的以左孩子为根节点的子树将不再是一个堆，因此parent将被刷新为当前左孩子的节点，而左孩子的值也将被刷新，如下图：

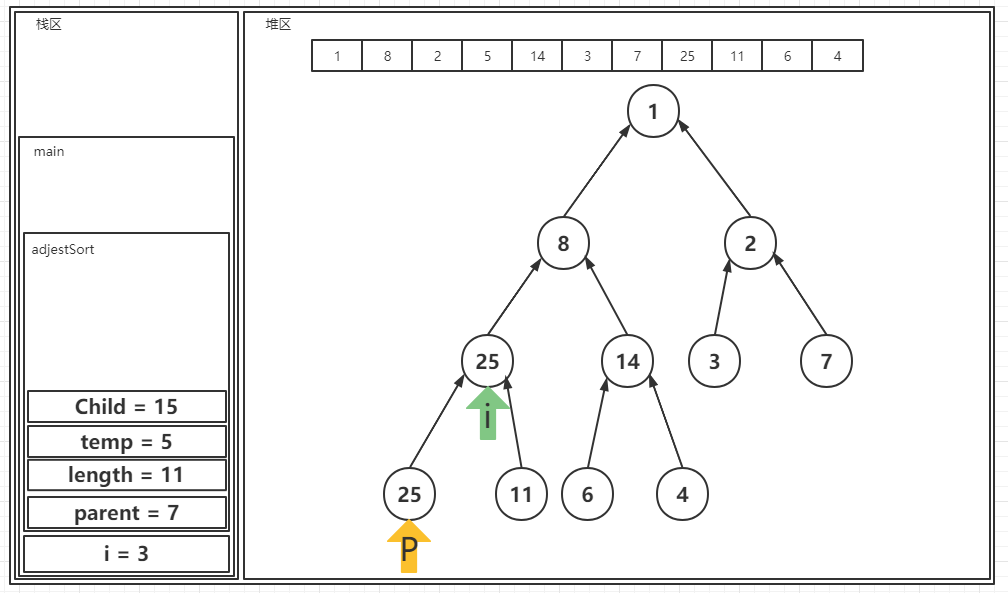
? 此时我们重新进行一轮新的循环，在循环开始的循环条件中，先会对Child的值和length做一次对比，我们会发现在此Child的值已经大于length了，因此循环将直接停止。在循环停止之后，会将temp的值直接赋予给当前parent指向的位置。这里需注意的是之前的图中没有画出parent标识，不是因为parent不存在，而是因为parent之前是和i位置重合的，这也引出了另一个新问题：i和parent的关系。i和parent的关系是，二者不是同一个，无论是从物理上还是从逻辑上，二者都不是同一个变量，parent是核心方法内的变量，i是核心方法外的变量，parent的变化不会影响到i的变化，我们需要注意到这一点。再将temp赋值给parent之后，之后我们继续向下执行：

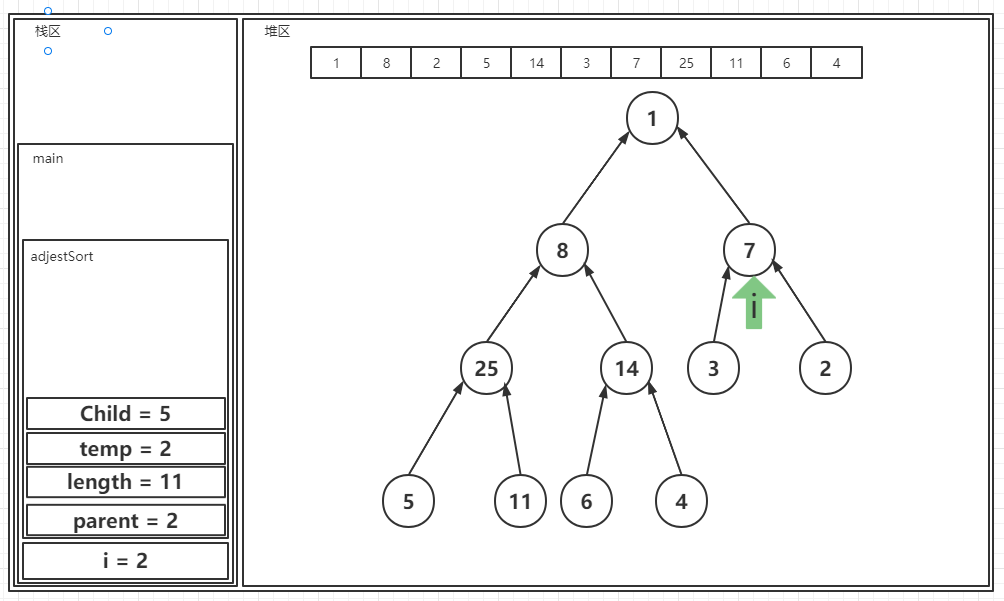
? 这次仍然会进入到核心方法中，进入到核心方法中之后，会发现右孩子节点是大于根节点的，因此发生交换，同时因为发生交换之后，右孩子节点没有子节点了，所以继续向下进行：

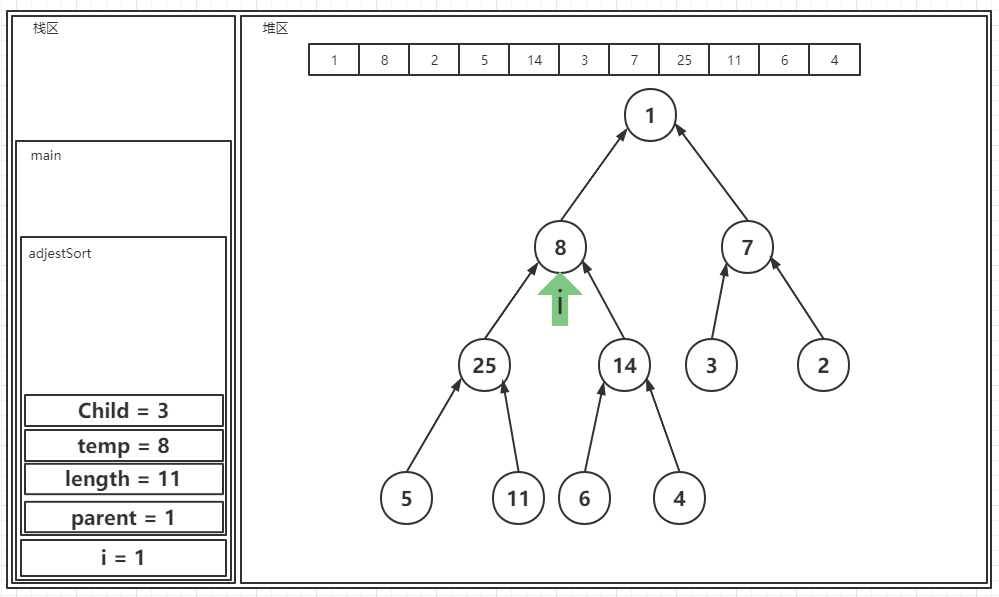
? 这时在进入到核心方法之后，首先会找到更大的左孩子节点，然后将其赋予到根节点的位置上，然后节点更新：

? 之后会再次进入一次循环，并且再次交换一次：

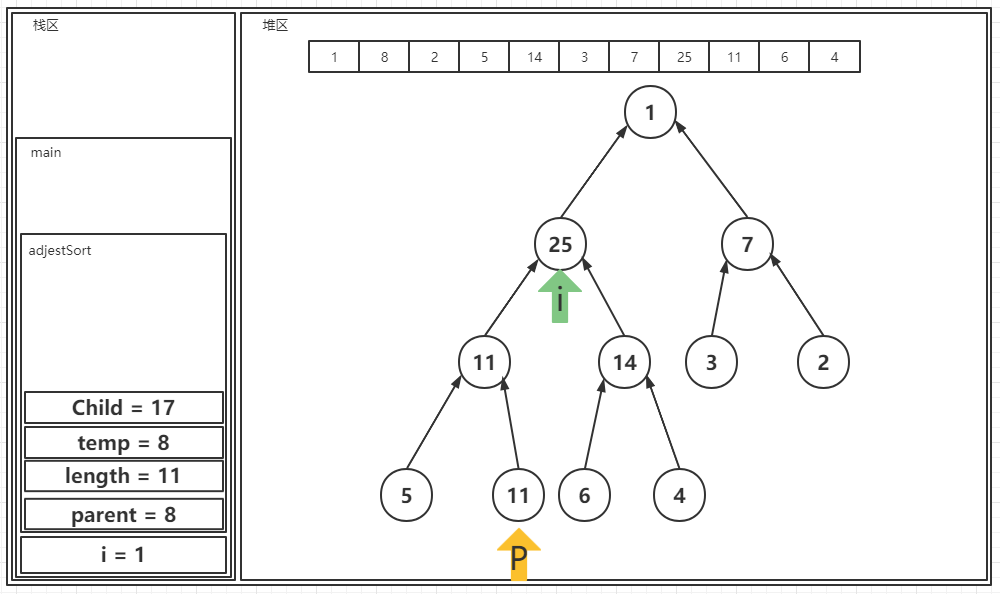
? 之后便不会再触发核心算法了，在最后将temp的值赋予给parent指向的节点：

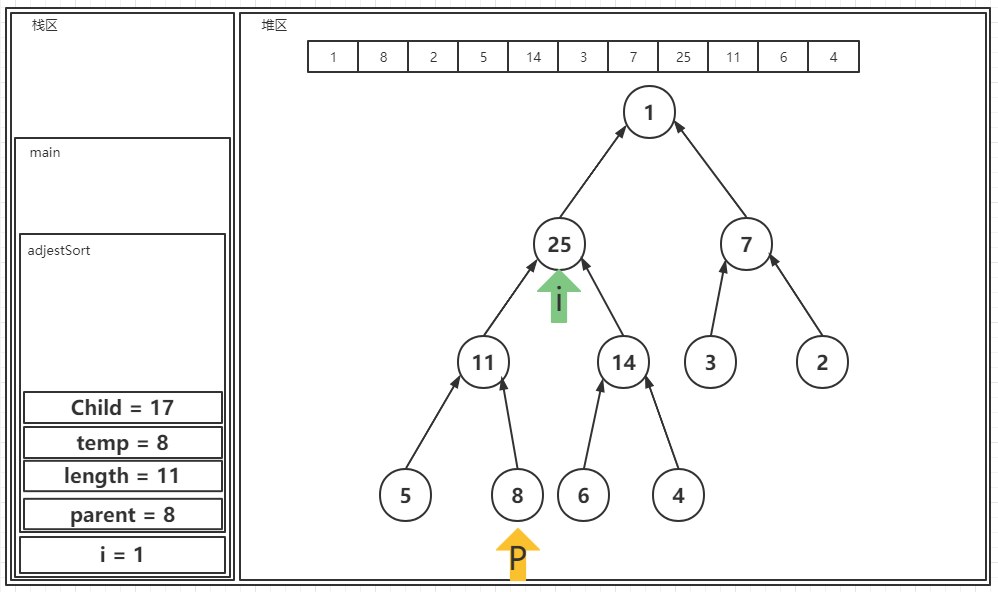
? 之后是对最后一个1进行比较：

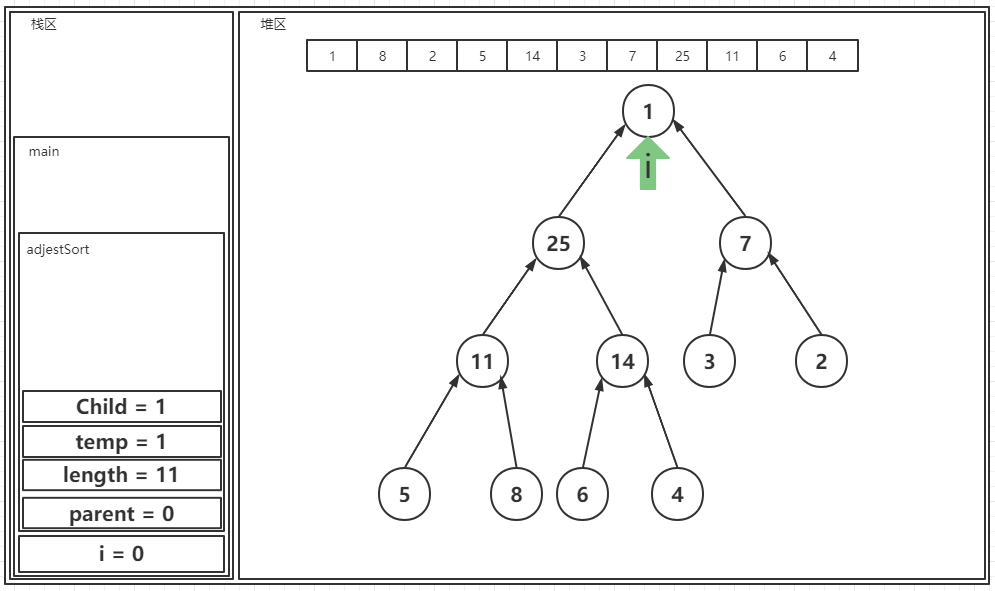
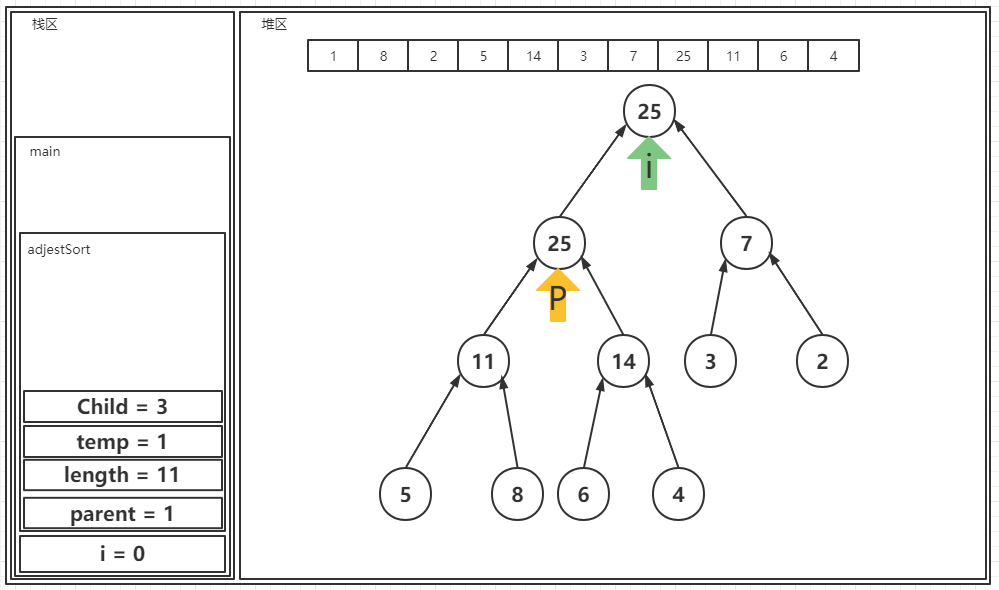
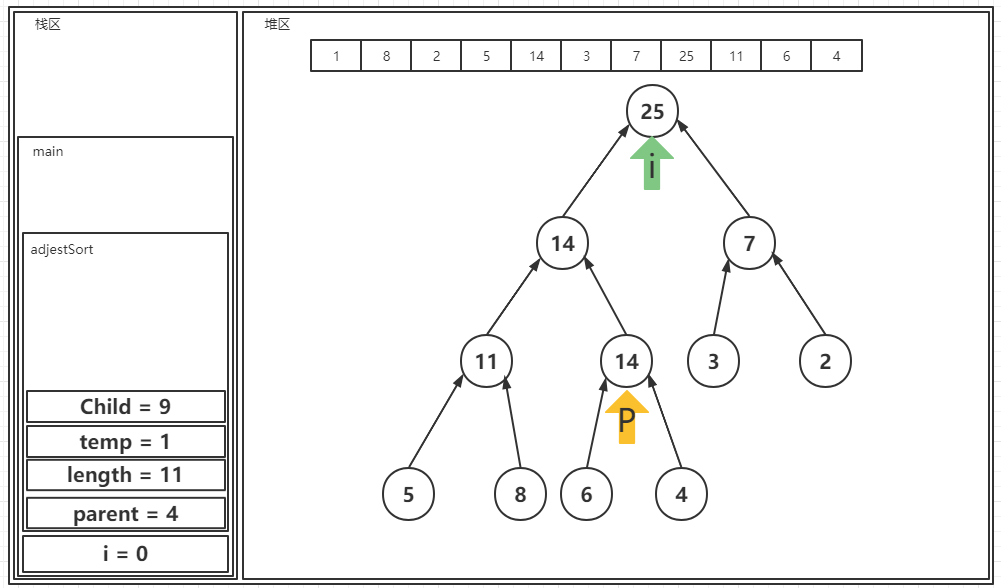
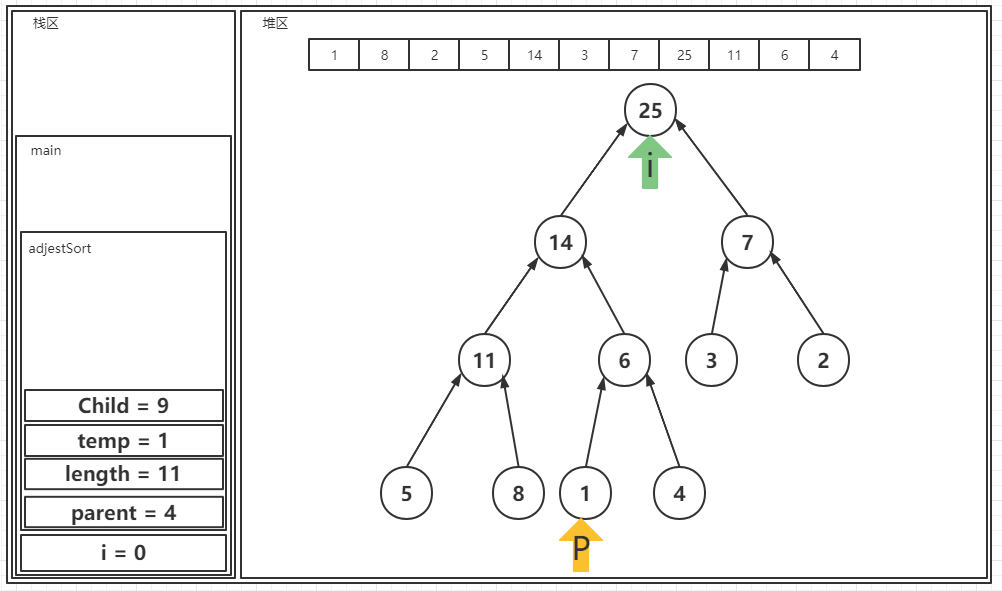
? 至此一个大顶堆完成。

3.堆排序过程

? 堆排序的过程就是先将堆顶元素和堆底元素进行交换：

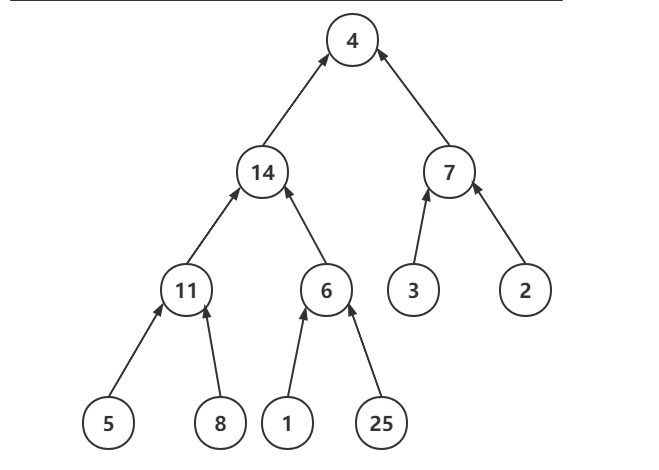
? 然后将排序规模缩小1，再对整个堆进行一次维护，重复这个过程即可。因为这次交换仅仅会让栈顶位置的数字变得不符合规则，因此仅仅使用一次维护就可以解决这个问题了。冠以堆排序以后我还会进行第三次和第四次学习。