开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 有上下界的（费用）网络流全解 -> 正文阅读

[数据结构与算法]有上下界的（费用）网络流全解

算法思想

一般的网络流只对边的容量要求上界，但是在一些模型中，边的容量被要求了下界，下界的出现要求流量不能从0开始，并且出现了新的问题，例如最小流，可行流等

无源汇上下界可行流

对于网络中的边 $< u, v >$ ，其可行流必然在上下界之内，为了解决网络中的可行流问题，首先就需要解决可行弧问题，即单条边的流量问题，但是由于下界的存在，使得一般的网络流处理方法无法使用，那么问题就变成了如何将下界进行转换使得原问题变成下界为0的普通网络流问题

举例如图，最左端点为源点，最右端点为汇点，左数值为下界，右数值为上界，定义必要弧 $C < u, v >$ 的容量为下界大小，则原网络就变成了下一张图的模样
在这里插入图片描述
在这张图中，下面三条边都为必要弧，上面三条边为原边上界-下界得到的数值，也就是可增量，因为必要弧的性质，那么对原问题可行流的求解就有了一个简单方法：在分离后的必要网络运行一次最大流算法，并且在走每条边的时候优先走必要流
但是，最大流算法在增广的时候选择边是盲目的，如果每次增广都要考虑是否有必要流，那么时间复杂度无疑会很大（因为会遍历）
在这里插入图片描述那么，现在问题就变成了如何能够修改网络结构使得必要弧本身就必须被经过？，也就是让必要弧本身必须满流
如果对网络流有过了解就可以知道，对于一个求解最大流的网络来说，源点的流量是必须满流的
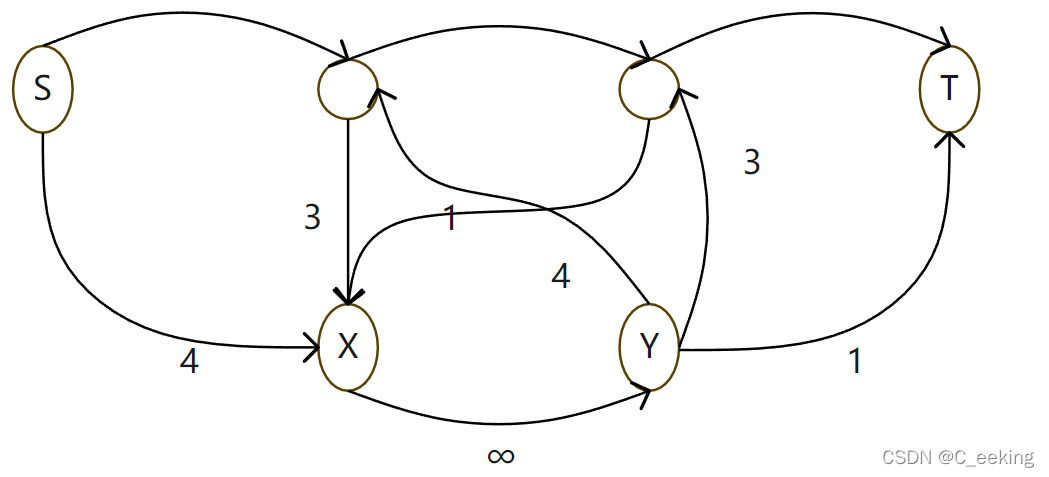
那么可以尝试添加一个源点X和汇点Y，假设一条不限上界的 $< X, Y >$ ，将所有必要弧 $< u, v >$ 拆成 $< u, X >, < Y, v >$ ，边的容量为必要弧容量，这样就建立出一个如下图的等价网络

在这里插入图片描述
去掉 $< X, Y >$ ，添加T到S的容量为∞的边，使得Y和X成为新的源点和汇点，则网络结构就变成了必要弧全部邻接于X与Y的普通网络，如下所示，必要弧满流便转化成最大流能够占满与Y相连的所有边的容量，则可行流的问题得到解决

在这里插入图片描述最大流的基础是可行流，在求解可行流的过程中就已经完成最大流求解的初始化，下面给出建图求解可行流及最大流的算法步骤（无源汇）

设以下变量：
$c a p (u, v) ：$ u->v的边容量
$u p (u, v) ：$ u->v上界
$l o w (u, v) ：$ u->下界
$s t (u) ：$ u所有出边下界和
$e d (u) ：$ u所有入边下界和

对于原有的网络 $G$ ，现在在 $G$ 的基础上构造附加网络 $D$
加入虚拟源/汇点 $S^{'}, T^{'}$
对于 $G$ 中的一条边 $(u, v)$ ，将 $(u, v)$ 加入 $D$ ， $c a p (u, v) = u p (u, v) ? l o w (u, v)$
对于 $G$ 中每个点 $u$ ，加入边 $(S^{'}, v)$ ， $c a p (S^{'}, v) = e d (v)$
对于 $G$ 中每个点 $u$ ，加入边 $(v, T^{'})$ ， $c a p (v, T^{'}) = s t (v)$
tflow为下界之和

求解 $S^{'}$ 到 $T^{'}$ 的最大流，如果最大流不等于tflow，则无可行流，若相等，代表至少可行流有解

代码（只包括了可行流实现，无源汇）

int ed[N],st[N],s,t,cnt,head[N],n,m,tflow,l[maxn];
 memset(head,-1,sizeof(head));
 for(int i=1; i<=m; i++) {
      int u,v,low,up;
      cin >>u>>v>>low>>up;
      Add(u,v,up-low,0);
      Add(v,u,0,0);
      st[u]+=low;
      ed[v]+=low;
      tflow+=low;
      l[i]=low;
  }
  s=0,t=n+1;
  for(int i=1; i<=n; i++) {//这里由于原图没有源点和汇点直接用虚拟节点了
      Add(s,i,ed[i],0);
      Add(i,s,0,0);
      Add(i,t,st[i],0);
      Add(t,i,0,0);
  }
  Add(t,s,inf,0);
  Add(s,t,0,0);
  //以上为建图
for(int i=1; i<=m; i++)//输出答案
       cout <<e[2*(i-1)].flow+l[i]<<endl;

有源汇上下界最大流

求解有源汇上下界最大流，需要先初始化图，利用可行流算法初始化，但是由于有源汇，需要在无源汇的基础上加入边(T,S)，容量为无穷大，判断完可行流后，之后为求解最大流，去掉所有和 $S^{'}$ ， $T^{'}$ 相连的边，双边都去掉，去掉(T,S)的附加边，其余边不变，包括流量，在这个去掉边的图中运行最大流算法即可，这种算法第一次得到的是可行流，第二次得到的是可行流基础上的最大流，需要将两者相加才能算出答案

当然也可以直接不删边跑源点到汇点的最大流，这样是直接算出来答案

有源汇上下界最小流

建立虚源汇和处理好下界分离之后，先跑一次最大流，然后源点和汇点接上无穷大的边，再跑一次最大流，最后最小流即为无穷大边的流量，因为整个图流量平滑，所以汇点的流入一定等于流出，但是t的出边只有这条无穷大边，所以最小流就是使得无穷大边流过的流量尽量小

由于第一次最大流时已经满足下界，那么再连上无穷大边之后，残余网络剩下的最大流就会尽可能小了

有源汇上下界最小费用可行流

有源汇上下界最小费用可行流，顾名思义，基于的模型是最小费用流与有源汇上下界最小流，如果把有源汇上下界最小流转换成一般的网络流，那么直接用最小费用流的模板就行了

先建一个有源汇上下界最大流的图，边权加上费用，然后加上所有的下界和对应费用的乘积之和，为了让有源汇上下界最大流的图中虚点间的边满流，就选用最小费用最大流，直接跑最小费用最大流即可，如果没有满流那就无解，最后答案是求出来的最小费用最大流的费用和+先前已经计算的下界和对应费用乘积之和

训练

LibreOJ #115

题目大意：略

思路：无源汇有上下界可行流模板题，注意答案输出的技巧

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e4+1212;
const int N=250;
const int inf=0x3f3f3f3f;
int ed[N],st[N],s,t,cnt,head[N],n,m,tflow,d[N],l[maxn],cur[N];
struct node {
    int next,to,cap,flow;
} e[maxn<<1];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;
}
bool BFS(int s,int t) {//分层
    memset(d,0,sizeof(d));
    for(int i=0; i<=n+1; i++)//复制每个点的head
        cur[i]=head[i];
    queue<int>q;
    q.push(s);
    d[s]=1;
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(!d[v]&&e[i].cap>e[i].flow) {//如果可以增流
                d[v]=d[u]+1;
                q.push(v);
                if(v==t)return 1;
            }
        }
    }
    return 0;
}
int DFS(int u,int flow,int t) {
    if(u==t)return flow;
    int res=flow;//res存储当前节点的可增流值
    for(int i=cur[u]; ~i&&res; i=e[i].next) {//遍历满足条件的邻边并增流
        cur[u]=i;//当前弧优化
        int v=e[i].to;
        if(d[v]==d[u]+1&&e[i].cap>e[i].flow) {
            int k=DFS(v,min(res,e[i].cap-e[i].flow),t);//获得最小的回溯流
            if(!k) {
                d[v]=0;
                continue;
            }
            e[i].flow+=k;//获得最小的回溯流后增流
            e[i^1].flow-=k;
            res-=k;//可增流值减少，因为已经有邻边增流
        }
    }
    return flow-res;//返回实际的总增流值
}
int Dinic(int s,int t) {
    int ans=0;//存储最大流
    while(BFS(s,t))for(int i=1;i<=n;i++)ans+=DFS(s,inf,t);
    return ans;
}
signed main() {
    //freopen("test.txt","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n>>m;
    memset(head,-1,sizeof(head));
    for(int i=1; i<=m; i++) {
        int u,v,low,up;
        cin >>u>>v>>low>>up;
        Add(u,v,up-low,0);
        Add(v,u,0,0);
        st[u]+=low;
        ed[v]+=low;
        tflow+=low;
        l[i]=low;//记录边的，不要求输出答案可以不要
    }
    s=0,t=n+1;
    for(int i=1; i<=n; i++) {
        Add(s,i,ed[i],0);
        Add(i,s,0,0);
        Add(i,t,st[i],0);
        Add(t,i,0,0);
    }
    if(Dinic(s,t)^tflow) cout <<"NO";
    else {
        cout <<"YES\n";
        for(int i=1; i<=m; i++)
            cout <<e[2*(i-1)].flow+l[i]<<endl;
    }
    return 0;
}

LibreOJ #116

题目大意：略

思路：有源汇上下界网络流模板题

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e4+1212;
const int N=250;
const int inf=0x3f3f3f3f;
int ed[N],st[N],s,t,sx,tx,cnt,head[N],n,m,tflow,d[N],cur[N];
struct node {
    int next,to,cap,flow;
} e[maxn<<1];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;
}
bool BFS(int s,int t) {//分层
    memset(d,0,sizeof(d));
    for(int i=0; i<=n+1; i++)//复制每个点的head
        cur[i]=head[i];
    queue<int>q;
    q.push(s);
    d[s]=1;
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(!d[v]&&e[i].cap>e[i].flow) {//如果可以增流
                d[v]=d[u]+1;
                q.push(v);
                if(v==t)return 1;
            }
        }
    }
    return 0;
}
int DFS(int u,int flow,int t) {
    if(u==t)return flow;
    int res=flow;//res存储当前节点的可增流值
    for(int i=cur[u]; ~i&&res; i=e[i].next) {//遍历满足条件的邻边并增流
        cur[u]=i;//当前弧优化
        int v=e[i].to;
        if(d[v]==d[u]+1&&e[i].cap>e[i].flow) {
            int k=DFS(v,min(res,e[i].cap-e[i].flow),t);//获得最小的回溯流
            if(!k) {
                d[v]=0;
                continue;
            }
            e[i].flow+=k;//获得最小的回溯流后增流
            e[i^1].flow-=k;
            res-=k;//可增流值减少，因为已经有邻边增流
        }
    }
    return flow-res;//返回实际的总增流值
}
int Dinic(int s,int t) {
    int ans=0;//存储最大流
    while(BFS(s,t))for(int i=1; i<=n; i++)ans+=DFS(s,inf,t);
    return ans;
}
signed main() {
    //freopen("test.txt","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n>>m>>s>>t;
    memset(head,-1,sizeof(head));
    for(int i=1; i<=m; i++) {
        int u,v,low,up;
        cin >>u>>v>>low>>up;
        Add(u,v,up-low,0);
        Add(v,u,0,0);
        st[u]+=low;
        ed[v]+=low;
        tflow+=low;
        //l[i]=low;
    }
    sx=0,tx=n+1;
    for(int i=1; i<=n; i++) {
        Add(sx,i,ed[i],0);
        Add(i,sx,0,0);
        Add(i,tx,st[i],0);
        Add(tx,i,0,0);
    }
    Add(t,s,inf,0);
    Add(s,t,0,0);
    if(Dinic(sx,tx)^tflow) cout <<"please go home to sleep";
    else 
        cout <<Dinic(s,t)<<endl;
    return 0;
}

LibreOJ #117

题目大意：略

思路：有上下界最小流模板

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e5+30000;
const int N=7e4+5;
const int inf=1e10;
int ed[N],st[N],s,t,sx,tx,cnt,head[N],n,m,tflow,d[N],cur[N];
struct node {
    int next,to,cap,flow;
} e[maxn<<1];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;
}
bool BFS(int s,int t) {//分层
    memset(d,0,sizeof(d));
    for(int i=0; i<=n+1; i++)//复制每个点的head
        cur[i]=head[i];
    queue<int>q;
    q.push(s);
    d[s]=1;
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(!d[v]&&e[i].cap>e[i].flow) {//如果可以增流
                d[v]=d[u]+1;
                q.push(v);
                if(v==t)return 1;
            }
        }
    }
    return 0;
}
int DFS(int u,int flow,int t) {
    if(u==t)return flow;
    int res=flow;//res存储当前节点的可增流值
    for(int i=cur[u]; ~i&&res; i=e[i].next) {//遍历满足条件的邻边并增流
        cur[u]=i;//当前弧优化
        int v=e[i].to;
        if(d[v]==d[u]+1&&e[i].cap>e[i].flow) {
            int k=DFS(v,min(res,e[i].cap-e[i].flow),t);//获得最小的回溯流
            if(!k) {
                d[v]=0;
                continue;
            }
            e[i].flow+=k;//获得最小的回溯流后增流
            e[i^1].flow-=k;
            res-=k;//可增流值减少，因为已经有邻边增流
        }
    }
    return flow-res;//返回实际的总增流值
}
int Dinic(int s,int t) {
    int ans=0;//存储最大流
    while(BFS(s,t))ans+=DFS(s,inf,t);
    return ans;
}
signed main() {
    //freopen("4.in","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n>>m>>s>>t;
    memset(head,-1,sizeof(head));
    for(int i=1; i<=m; i++) {
        int u,v,low,up;
        cin >>u>>v>>low>>up;
        Add(u,v,up-low,0);
        Add(v,u,0,0);
        st[u]+=low;
        ed[v]+=low;
        tflow+=low;
    }
    sx=0,tx=n+1;
    for(int i=1; i<=n; i++) {
        Add(sx,i,ed[i],0);
        Add(i,sx,0,0);
        Add(i,tx,st[i],0);
        Add(tx,i,0,0);
    }
    tflow-=Dinic(sx,tx);
    Add(t,s,inf,0);
    Add(s,t,0,0);
    tflow-=Dinic(sx,tx);
    if(tflow) cout <<"please go home to sleep";
    else
        cout <<e[cnt-2].flow;
    return 0;
}

LuoguP5192

题目大意：略

思路：题意很难理解，但是建的图还是很简单的，注意到汇点的边只有下界没有上界
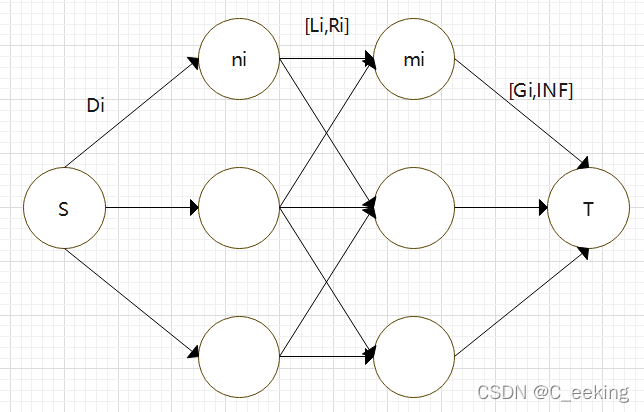
在这里插入图片描述

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int inf=0x3f3f3f3f;
const int maxn=4e5+5;
const int N=2121;
int ed[N],st[N],s,t,sx,tx,cnt,head[N],n,m,tflow,d[N],cur[N];
struct node {
    int next,to,cap,flow;
} e[maxn];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;
}
bool BFS(int s,int t) {//分层
    memset(d,0,sizeof(d));
    for(int i=0; i<=n+m+3; i++)//复制每个点的head，注意节点个数
        cur[i]=head[i];
    queue<int>q;
    q.push(s);
    d[s]=1;
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(!d[v]&&e[i].cap>e[i].flow) {//如果可以增流
                d[v]=d[u]+1;
                q.push(v);
                if(v==t)return 1;
            }
        }
    }
    return 0;
}
int DFS(int u,int flow,int t) {
    if(u==t)return flow;
    int res=flow;//res存储当前节点的可增流值
    for(int i=cur[u]; ~i&&res; i=e[i].next) {//遍历满足条件的邻边并增流
        cur[u]=i;//当前弧优化
        int v=e[i].to;
        if(d[v]==d[u]+1&&e[i].cap>e[i].flow) {
            int k=DFS(v,min(res,e[i].cap-e[i].flow),t);//获得最小的回溯流
            if(!k) {
                d[v]=0;
                continue;
            }
            e[i].flow+=k;//获得最小的回溯流后增流
            e[i^1].flow-=k;
            res-=k;//可增流值减少，因为已经有邻边增流
        }
    }
    return flow-res;//返回实际的总增流值
}
int Dinic(int s,int t) {
    int ans=0;//存储最大流
    while(BFS(s,t))
        ans+=DFS(s,inf,t);
    return ans;
}
signed main() {
    //freopen("test.txt","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(0);
    while(cin >>n>>m) {
        memset(head,-1,sizeof(head));
        memset(st,0,sizeof(st));
        memset(ed,0,sizeof(ed));
        cnt=tflow=0;
        s=0,t=n+m+1,sx=t+1,tx=t+2;//源汇和虚节点
        for(int i=1; i<=m; i++) {//和汇点连接
            int low,v=n+i;
            cin >>low;
            Add(v,t,inf,0);
            Add(t,v,0,0);
            st[v]+=low;
            ed[t]+=low;
            tflow+=low;
        }
        for(int u=1; u<=n; u++) {
            int c,f;
            cin >>c>>f;
            Add(s,u,f,0);//源点流量
            Add(u,s,0,0);
            while(c--) {//中间的流量
                int v,low,up;
                cin >>v>>low>>up;
                v=v+n+1;
                Add(u,v,up-low,0);
                Add(v,u,0,0);
                st[u]+=low;
                ed[v]+=low;
                tflow+=low;
            }
        }
        for(int i=s; i<=t; i++) {//增加虚点
            Add(sx,i,ed[i],0);
            Add(i,sx,0,0);
            Add(i,tx,st[i],0);
            Add(tx,i,0,0);
        }
        Add(t,s,inf,0);
        Add(s,t,0,0);
        if(Dinic(sx,tx)^tflow)cout <<"-1\n\n";
        else cout <<Dinic(s,t)<<endl<<endl;
    }
    return 0;
}

LuoguP4843

题目大意：略

思路：有源汇上下界网络流，注意建图，以及Dinic的节点数量

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e4+1212;
const int N=250;
const int inf=0x3f3f3f3f;
int ed[N],st[N],s,t,sx,tx,cnt,head[N],n,m,tflow,d[N],cur[N];
struct node {
    int next,to,cap,flow;
} e[maxn<<1];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;
}
bool BFS(int s,int t) {//分层
    memset(d,0,sizeof(d));
    for(int i=0; i<=n+3; i++)//复制每个点的head
        cur[i]=head[i];
    queue<int>q;
    q.push(s);
    d[s]=1;
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(!d[v]&&e[i].cap>e[i].flow) {//如果可以增流
                d[v]=d[u]+1;
                q.push(v);
                if(v==t)return 1;
            }
        }
    }
    return 0;
}
int DFS(int u,int flow,int t) {
    if(u==t)return flow;
    int res=flow;//res存储当前节点的可增流值
    for(int i=cur[u]; ~i&&res; i=e[i].next) {//遍历满足条件的邻边并增流
        cur[u]=i;//当前弧优化
        int v=e[i].to;
        if(d[v]==d[u]+1&&e[i].cap>e[i].flow) {
            int k=DFS(v,min(res,e[i].cap-e[i].flow),t);//获得最小的回溯流
            if(!k) {
                d[v]=0;
                continue;
            }
            e[i].flow+=k;//获得最小的回溯流后增流
            e[i^1].flow-=k;
            res-=k;//可增流值减少，因为已经有邻边增流
        }
    }
    return flow-res;//返回实际的总增流值
}
int Dinic(int s,int t) {
    int ans=0;//存储最大流
    while(BFS(s,t))ans+=DFS(s,inf,t);
    return ans;
}
signed main() {
    //freopen("test.txt","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n;
    memset(head,-1,sizeof(head));
    s=0,t=n+1,sx=t+1,tx=t+2;
    for(int u=1; u<=n; u++) {
        int m;
        cin >>m;
        Add(s,u,inf,0);
        Add(u,s,0,0);
        Add(u,t,inf,0);
        Add(t,u,0,0);
        st[u]+=m;
        while(m--) {
            int v;
            cin >>v;
            Add(u,v,inf,0);
            Add(v,u,0,0);
            ed[v]++;
        }
    }
    for(int i=1; i<=n; i++) {
        Add(sx,i,ed[i],0);
        Add(i,sx,0,0);
        Add(i,tx,st[i],0);
        Add(tx,i,0,0);
    }
    Dinic(sx,tx);
    Add(t,s,inf,0);
    Add(s,t,0,0);
    Dinic(sx,tx);
    cout <<e[cnt-2].flow;
    return 0;
}

LuoguP4043

题目大意：略

思路：带上界的费用流模板题，第一遍的时候只建立了结局与汇点的边，应该建所有的实点与汇点的边

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e4+5;
const int N=1212;
const int inf=0x3f3f3f3f;
int ed[N],st[N],s,t,sx,tx,cnt,head[N],n,m,tflow,dis[N],pre[N];
bool vis[N];
struct node {
    int next,to,cap,flow,pay;
} e[maxn<<1];
void Add(int from,int to,int cap,int flow,int pay) {
    e[cnt].to=to;
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].pay=pay;
    e[cnt].next=head[from];
    head[from]=cnt++;
}
bool SPFA(int s,int t) {
    queue<int>q;
    memset(vis,0,sizeof(vis));
    memset(pre,-1,sizeof(pre));
    memset(dis,0x3f,sizeof(dis));
    dis[s]=0;
    vis[s]=1;
    q.push(s);
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        vis[u]=0;
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(e[i].cap>e[i].flow&&dis[v]>dis[u]+e[i].pay) {
                dis[v]=dis[u]+e[i].pay;
                pre[v]=i;
                if(vis[v])continue;
                vis[v]=1;
                q.push(v);
            }
        }
    }
    return pre[t]!=-1;
}
int MCMF(int s,int t) {
    int mincost=0;
    while(SPFA(s,t)) {
        int d=inf,v=t;
        while(v!=s) {
            int i=pre[v];
            d=min(d,e[i].cap-e[i].flow);//可增加的流量
            v=e[i^1].to;//换点
        }
        v=t;
        while(v!=s) {
            int i=pre[v];
            e[i].flow+=d;
            e[i^1].flow-=d;//实流
            v=e[i^1].to;
        }
        mincost+=dis[t]*d;
    }
    return mincost;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n;
    memset(head,-1,sizeof(head));
    s=0,t=n+1,sx=t+1,tx=t+2;
    Add(s,1,inf,0,0),Add(1,s,0,0,0);
    for(int u=1; u<=n; u++) {
        cin >>m;
        while(m--) {
            int v,p;
            cin >>v>>p;
            Add(u,v,inf,0,p);
            Add(v,u,0,0,-p);
            st[u]++,ed[v]++;//这里的下界都是1
            tflow+=p;//加上1*p
        }
    }
    Add(t,s,inf,0,0);
    Add(s,t,0,0,0);
    for(int i=1; i<=n; i++) {
        Add(sx,i,ed[i],0,0);
        Add(i,sx,0,0,0);
        Add(i,tx,st[i],0,0);
        Add(tx,i,0,0,0);
        Add(i,t,inf,0,0);//需要与汇点连接，不要想当然
        Add(t,i,0,0,0);
    }
    cout <<MCMF(sx,tx)+tflow;
    return 0;
}

LuoguP4311

题目大意：略

思路：每一行每一列需要拆点，拆成入点和出点，拆点间不需要连接，根据每一行每一列的连通关系连接对应的出点与入点，入点有下界，出点有下界，详见代码

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e5+30000;
const int N=1e4+5;
const int inf=1e10;
int ed[N],st[N],s,t,sx,tx,k,cnt,head[N],n,m,tflow,d[N],cur[N];
int low[N],up[N];
bool vis[N][N];
struct node {
    int next,to,cap,flow;
} e[maxn<<1];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;
}
bool BFS(int s,int t) {//分层
    memset(d,0,sizeof(d));
    for(int i=0; i<=t+2; i++)//复制每个点的head
        cur[i]=head[i];
    queue<int>q;
    q.push(s);
    d[s]=1;
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(!d[v]&&e[i].cap>e[i].flow) {//如果可以增流
                d[v]=d[u]+1;
                q.push(v);
                if(v==t)return 1;
            }
        }
    }
    return 0;
}
int DFS(int u,int flow,int t) {
    if(u==t)return flow;
    int res=flow;//res存储当前节点的可增流值
    for(int i=cur[u]; ~i&&res; i=e[i].next) {//遍历满足条件的邻边并增流
        cur[u]=i;//当前弧优化
        int v=e[i].to;
        if(d[v]==d[u]+1&&e[i].cap>e[i].flow) {
            int k=DFS(v,min(res,e[i].cap-e[i].flow),t);//获得最小的回溯流
            if(!k) {
                d[v]=0;
                continue;
            }
            e[i].flow+=k;//获得最小的回溯流后增流
            e[i^1].flow-=k;
            res-=k;//可增流值减少，因为已经有邻边增流
        }
    }
    return flow-res;//返回实际的总增流值
}
int Dinic(int s,int t) {
    int ans=0;//存储最大流
    while(BFS(s,t))ans+=DFS(s,inf,t);
    return ans;
}
signed main() {
    //freopen("4.in","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n>>m>>k;
    s=0,t=2*(n+m)+1,sx=t+1,tx=t+2;//源点，汇点，虚源汇
    memset(head,-1,sizeof(head));
    for(int i=1; i<=n+m; i++) {
        cin >>low[i];
        up[i]=i<=n?m:n;//初始化上界
    }
    for(int i=1; i<=k; i++) {
        int x,y;
        cin >>x>>y;
        up[x]--;//上界-1
        up[y+n]--;
        vis[x][y]=1;
        vis[y][x]=1;
    }
    for(int i=1; i<=n+m; i++) {
        Add(s,i,up[i]-low[i],0);
        Add(i,s,0,0);
        Add(i+n+m,t,up[i]-low[i],0);
        Add(t,i+n+m,0,0);
        Add(i,i+n+m,inf,0);
        Add(i+n+m,i,0,0);
        st[s]+=low[i],st[i+n+m]+=low[i];//源点和出点都有下界流
        ed[i]+=low[i],ed[t]+=low[i];
        tflow+=2*low[i];
    }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++) {
            if(!vis[i][j]) {//入点和出点连接
                Add(i,j+n+m,1,0);
                Add(j+n+m,i,0,0);
                Add(j+n,i+n+m,1,0);
                Add(i+n+m,j+n,0,0);
                vis[i][j]=vis[j][i]=1;
            }
        }
    for(int i=0; i<=2*(n+m)+1; i++) {
        Add(sx,i,ed[i],0);
        Add(i,sx,0,0);
        Add(i,tx,st[i],0);
        Add(tx,i,0,0);
    }
    tflow-=Dinic(sx,tx);
    Add(t,s,inf,0);
    Add(s,t,0,0);
    tflow-=Dinic(sx,tx);
    if(tflow) cout <<"JIONG!";
    else
        cout <<e[cnt-2].flow/2;
    return 0;
}

LuoguP4194

题目大意：略

思路：题面的具体意思可以参考文章末的题解，这里只说一下建图
考虑二分答案，那么就是求 $|\sum A_{i,j}-\sum B_{i,j}|\le mid$ ，可以得到 $\sum B_{i,j}$ 的范围： $[|\sum A_{i,j}-mid,\sum A_{i,j}+mid|]$ ，每一行B的和在A行之和上下加mid间
对每一行每一列单独使用一个点，源点向每一行连下界为A行之和-mid，上界为A行之和+mid，每一列同理，然后每一行与每一列连下界L，上界R的边

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+1212;
const int N=2121;
const int inf=1e10;
int ed[N],st[N],s,t,sx,tx,ss,cnt,head[N],n,m,tflow,d[N],cur[N],val[N],k,L,R;
int sumh[N],suml[N];
vector<int>graph[N];
struct node {
    int next,to,cap,flow;
} e[maxn<<1];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;
}
bool BFS(int s,int t) {//分层
    memset(d,0,sizeof(d));
    for(int i=0; i<=tx; i++)//复制每个点的head
        cur[i]=head[i];
    queue<int>q;
    q.push(s);
    d[s]=1;
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(!d[v]&&e[i].cap>e[i].flow) {//如果可以增流
                d[v]=d[u]+1;
                q.push(v);
                if(v==t)return 1;
            }
        }
    }
    return 0;
}
int DFS(int u,int flow,int t) {
    if(u==t)return flow;
    int res=flow;//res存储当前节点的可增流值
    for(int i=cur[u]; ~i&&res; i=e[i].next) {//遍历满足条件的邻边并增流
        cur[u]=i;//当前弧优化
        int v=e[i].to;
        if(d[v]==d[u]+1&&e[i].cap>e[i].flow) {
            int k=DFS(v,min(res,e[i].cap-e[i].flow),t);//获得最小的回溯流
            if(!k) {
                d[v]=0;
                continue;
            }
            e[i].flow+=k;//获得最小的回溯流后增流
            e[i^1].flow-=k;
            res-=k;//可增流值减少，因为已经有邻边增流
        }
    }
    return flow-res;//返回实际的总增流值
}
int Dinic(int s,int t) {
    int ans=0;//存储最大流
    while(BFS(s,t))for(int i=1; i<=n; i++)ans+=DFS(s,inf,t);
    return ans;
}
bool Judge(int stand) {
    memset(head,-1,sizeof(head));
    memset(st,0,sizeof(st));
    memset(ed,0,sizeof(ed));
    s=0,t=n+m+1,sx=t+1,tx=t+2;
    tflow=cnt=0;
    for(int i=1; i<=n; i++) {
        Add(s,i,2*stand,0),Add(i,s,0,0);
        st[s]+=max(sumh[i]-stand,0*1ll);//强制下界为正
        ed[i]+=max(sumh[i]-stand,0*1ll);//同上
        tflow+=max(sumh[i]-stand,0*1ll);//同上
        for(int j=1; j<=m; j++) {
            Add(i,j+n,R-L,0),Add(j+n,i,0,0);
            st[i]+=L;
            ed[j+n]+=L;
            tflow+=L;
        }
    }
    for(int i=1; i<=m; i++) {
        Add(i+n,t,2*stand,0),Add(t,i+n,0,0);
        st[i+n]+=max(suml[i]-stand,0*1ll);
        ed[t]+=max(suml[i]-stand,0*1ll);
        tflow+=max(suml[i]-stand,0*1ll);
    }
    Add(t,s,inf,0),Add(s,t,0,0);
    for(int i=s; i<=t; i++) {
        Add(sx,i,ed[i],0),Add(i,sx,0,0);
        Add(i,tx,st[i],0),Add(tx,i,0,0);
    }
    return tflow==Dinic(sx,tx);
}
signed main() {
    //freopen("test.txt","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n>>m;
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++) {
            int x;
            cin >>x;
            sumh[i]+=x;//行和
            suml[j]+=x;//列和
        }
    cin >>L>>R;
    int l=0,r=inf,res=0;
    while(l<=r) {
        int mid=(l+r)/2;
        if(Judge(mid)) {//如果这个解合法，尝试更小的解
            res=mid;
            r=mid-1;
        } else
            l=mid+1;
    }
    cout <<res;
    return 0;
}

LuoguP4589

题目大意：略

思路：尝试二分答案，对于每个答案，小于这个答案的节点都被建图，然后判断这个答案是否可行（是否能满流），每个题目拆点，对于题目的先后顺序代表出点连入汇点

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+1212;
const int N=2121;
const int inf=1e10;
int ed[N],st[N],s,t,sx,tx,ss,cnt,head[N],n,m,tflow,d[N],cur[N],val[N],k;
vector<int>graph[N];
struct node {
    int next,to,cap,flow;
} e[maxn<<1];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;
}
bool BFS(int s,int t) {//分层
    memset(d,0,sizeof(d));
    for(int i=0; i<=tx; i++)//复制每个点的head
        cur[i]=head[i];
    queue<int>q;
    q.push(s);
    d[s]=1;
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(!d[v]&&e[i].cap>e[i].flow) {//如果可以增流
                d[v]=d[u]+1;
                q.push(v);
                if(v==t)return 1;
            }
        }
    }
    return 0;
}
int DFS(int u,int flow,int t) {
    if(u==t)return flow;
    int res=flow;//res存储当前节点的可增流值
    for(int i=cur[u]; ~i&&res; i=e[i].next) {//遍历满足条件的邻边并增流
        cur[u]=i;//当前弧优化
        int v=e[i].to;
        if(d[v]==d[u]+1&&e[i].cap>e[i].flow) {
            int k=DFS(v,min(res,e[i].cap-e[i].flow),t);//获得最小的回溯流
            if(!k) {
                d[v]=0;
                continue;
            }
            e[i].flow+=k;//获得最小的回溯流后增流
            e[i^1].flow-=k;
            res-=k;//可增流值减少，因为已经有邻边增流
        }
    }
    return flow-res;//返回实际的总增流值
}
int Dinic(int s,int t) {
    int ans=0;//存储最大流
    while(BFS(s,t))for(int i=1; i<=n; i++)ans+=DFS(s,inf,t);
    return ans;
}
bool Judge(int stand) {
    memset(head,-1,sizeof(head));
    memset(st,0,sizeof(st));
    memset(ed,0,sizeof(ed));
    cnt=0;
    ss=2*m+1,t=2*m+2,sx=t+1,tx=t+2,s=0,tflow=0;
    Add(s,ss,n+1,0),Add(ss,s,0,0);
    for(int i=1; i<=m; i++)
        Add(ss,i,n+1,0),Add(i,ss,0,0),Add(i+m,t,n+1,0),Add(t,i+m,0,0);
    for(int i=1; i<=m; i++) {
        int len=graph[i].size();
        for(int j=0; j<len; j++)
            Add(i+m,graph[i][j],n+1,0),Add(graph[i][j],i+m,0,0);
    }
    for(int i=1; i<=m; i++) {//关键部分
        if(val[i]<stand) {//只有必选的边才使用
            st[i]++;
            ed[i+m]++;
            tflow++;
            Add(i,i+m,n,0),Add(i+m,i,0,0);
        } else
            Add(i,i+m,n+1,0),Add(i+m,i,0,0);
    }
    for(int i=1; i<=t; i++) {
        if(ed[i])
            Add(sx,i,ed[i],0),Add(i,sx,0,0);
        if(st[i])
            Add(i,tx,st[i],0),Add(tx,i,0,0);
    }
    Add(t,s,inf,0),Add(s,t,0,0);
    return tflow==Dinic(sx,tx);
}
signed main() {
    //freopen("test.txt","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n>>m;
    int mx=0;
    for(int i=1; i<=m; i++) {
        cin >>val[i]>>k;
        while(k--) {
            int x;
            cin >>x;
            graph[i].push_back(x);
        }
    }
    int low=0,high=inf,res=inf;
    while(low<=high) {
        int mid=(low+high)/2;
        if(Judge(mid)) {//这里不要写错了，判断为真代表不连一些边能够满流
            res=mid;
            low=mid+1;
        } else
            high=mid-1;
    }
    res==inf?cout <<"AK":cout <<res;
    return 0;
}

2021昆明B

题目大意：n行m列的棋盘，对于棋盘上的每一个格子，选择放黑或者白或者空，对于每个位置 $i\in [1,n]，j\in [1,m]$ ，放一个黑会得到 $sb_{i,j}$ 的价值，放一个白会得到 $sw_{i,j}$ ，放空白则不得分，每个位置只能放一个
定义 $b_i$ 是第i行的黑块数， $B_i$ 是第i列的黑数， $w_i$ 是第i行的白数， $W_i$ 是第i列的白数，这四个变量必须满足

$i\in [1,n],b_i-w_i\in[l_i,r_i]$
$j\in [1,m],B_j-W_j\in[L_j,R_j]$

现在想要最小化获得的价值，求出最少能获得多少价值

思路：万恶之源，就是这道题让我陷入了学习网络流万劫不复的深渊
本题对应的模型应该是有上下界的最小费用流
处理负圈需要强制满流，对每一行和列单独开点，初始假设全是白色，那么剩下的操作就是撤销白色和涂黑，给定的限制使得每一行/列差值需要满足于一个区间，建边的时候是撤销白/加黑，实际上都是给黑-白这个整体+1，由于存在负边，可以强制满流来处理，也可以如文章末的题解那样处理

代码

#include<cstdio>
#include<iostream>
#include<queue>
using namespace std;
const int INF=1e9;
const int MAXN=500005;
int n=0,m=0,s=0,t=0;
int tot=1,head[MAXN]={},pre[MAXN]={},flow[MAXN]={};
int maxflow=0,mincost=0;
struct edge
{
	int to;
	int next;
	int f;
	int c;
};
edge E[MAXN]={};
void add(int u,int v,int f,int c)
{
	E[++tot].to=v;
	E[tot].f=f;
	E[tot].c=c;
	E[tot].next=head[u];
	head[u]=tot;

	E[++tot].to=u;
	E[tot].f=0;
	E[tot].c=-c;
	E[tot].next=head[v];
	head[v]=tot;
}
int vis[MAXN]={},dis[MAXN]={};
bool SPFA()
{
	queue<int> q;
	for(int i=0;i<=t;++i){
		dis[i]=INF;
		flow[i]=INF;
		vis[i]=0;
	}
	pre[t]=-1;
	q.push(s);vis[s]=1;dis[s]=0;
	while(!q.empty()){
		int x=q.front();
		q.pop();
		vis[x]=0;
		for(int i=head[x];i;i=E[i].next){
			int v=E[i].to;
			if(E[i].f && dis[v]>dis[x]+E[i].c){
				dis[v]=dis[x]+E[i].c;
				pre[v]=i;
				flow[v]=min(flow[x],E[i].f);
				if(!vis[v]){
					q.push(v);
					vis[v]=1;
				}
			}
		}
	}
	return pre[t]!=-1;
}
void mcmf()
{
	while(SPFA()){
		int x=t;
		maxflow+=flow[t];
		mincost+=flow[t]*dis[t];
		while(x!=s){
			int p=pre[x];
			E[p].f-=flow[t];
			E[p^1].f+=flow[t];
			x=E[p^1].to;
		}
	}
}
int In[MAXN]={},Out[MAXN]={};
int D[MAXN]={};
int sb[60][60]={},sw[60][60]={};
int main()
{
	scanf("%d%d",&n,&m);
	int ans=0;
	int s1=0,t1=n+m+1;
	int S=n+m+4,T=n+m+5;
	for(int i=1;i<=n;++i){
		for(int j=1;j<=m;++j){
			scanf("%d",&sb[i][j]);
		}
	}
	for(int i=1;i<=n;++i){
		for(int j=1;j<=m;++j){
			scanf("%d",&sw[i][j]);
			ans+=sw[i][j];
		}
	}
	int l=0,r=0;
	for(int i=1;i<=n;++i){
		scanf("%d%d",&l,&r);//上下界为[m+l,m+r];
		add(s1,i,r-l,0);
		In[i]+=m+l;Out[s1]+=m+l;
	}
	for(int i=1;i<=m;++i){
		scanf("%d%d",&l,&r);//上下界为[n+l,n+r]
		add(i+n,t1,r-l,0);
		In[t1]+=n+l;Out[i+n]+=n+l;
	}
	for(int i=1;i<=n;++i){
		for(int j=1;j<=m;++j){
			add(j+n,i,1,sw[i][j]);//add(i,j+n,1,-sw[i][j]) 强制满流 处理负圈
			D[i]-=1;D[j+n]+=1;
			mincost+=-sw[i][j];
			add(i,j+n,1,sb[i][j]);
		}
	}
	s=n+m+2,t=n+m+3;
	for(int i=0;i<=n+m+1;++i){
		if(In[i]>Out[i]){
			add(s,i,In[i]-Out[i],0);
		}
		if(Out[i]>In[i]){
			add(i,t,Out[i]-In[i],0);
		}
	}
	add(t1,s1,INF,0);
	for(int i=0;i<=t;++i){
		if(D[i]>0){
			add(S,i,D[i],0);
		}
		if(D[i]<0){
			add(i,T,-D[i],0);
		}
	}
	add(t,s,INF,0);
	s=S,t=T;
	mcmf();
	s=n+m+2,t=n+m+3;
	E[tot].f=0;E[tot-1].f=0;
	mcmf();
	printf("%d",ans+mincost);
	return 0;
}

总结

上下界网络流问题最关键的在于建图，怎样处理下界，怎样处理源点与汇点，上下界网络流大多由这样几个模型：

棋盘/矩阵模型，这一类模型的建图大多是行/列有限制，单点存在限制，建图方法是对行列单独开点，汇连行，列连源，然后行列间的单点使用这个点的L和R直接限制即可
负下界模型，这种模型与很多其他模型都可以匹配，对于存在负值的下界，要么强制为正，要么强制满流处理
二分模型，这种模型经常和负下界模型结合，对于答案二分，尝试可行解，用可行解建图时就可能出现负下界
区间/时间点模型，一种很特殊的模型，给出的流量不是两点间的，而是一个区间的，例如志愿者招募问题，对于给出的一个点，其流量在一个区间[l,r]内，那么可以直接在l到r+1间建边，至于相邻的点之间直接根据约束建即可