递归与递推
递归就是自己调用自己。
printf和scanf的速度比cin和cout要快
如果输入输出的规模小于10的5次方,速度没有太大区别,如果大于10的5次方,最好是用printf和scanf(相差大概一倍)
参数有两个位置,全局参数和形参。
斐波那契数列
#include<iostream>//有cin和cout
#include<cstring>//有memset
#include<cstdio>//有scanf和printf
using namespace std;
int f(int n)//每个递归都会实现一棵递归搜索树,然后树的子结点都是边界(n==1或n==2)
{
if(n==1) return 0;
if(n==2) return 1;
else
{
return f(n-1)+f(n-2);
}
}
int main()
{
int n;
cin>>n;//输入:5
int i = 0 ;
for(i = 1;i <= n-1 ;i++)
{
cout <<f(i)<<" ";
}
cout<<f(i);//输出:0 1 1 2 3
return 0;
}
使用递推的方法:
递归是将一个问题分解成一系列同种子问题;递推正好相反,是通过解决子问题然后推算原问题。
int main()
{
int n;
cin >> n;
int arr[20];
arr[1] = 0;
arr[2] = 1;
for (int i = 3; i <= n; i++)
{
arr[i] = arr[i - 1] + arr[i - 2];
}
for (int i = 1; i <= n; i++)
{
cout << arr[i] << " ";
}
return 0;
}
这个可以进行优化,从空间的角度进行优化
原先使用的是保存的数组,经过优化以后可以只保存两个数。
int main()
{
int n;
cin >> n;
int a = 0;
int b = 1;
for (int i = 1; i <= n; i++)
{
cout << a << " ";//每次只打印一个数,a。
int fn = a + b;
a = b;
b = fn;
}
return 0;
}
//只需要存储a,b两个变量。
常用的2的次方表:
2的63次方 = 10的18次方
2的20次方 = 10的6次方
2的16次方 = 65536
2的15次方 = 32768
使用递归需要
1,创建递归搜索树
2,定义边界,因为最后的值都是要回归到边界上来的。
递归实现(指数型)枚举
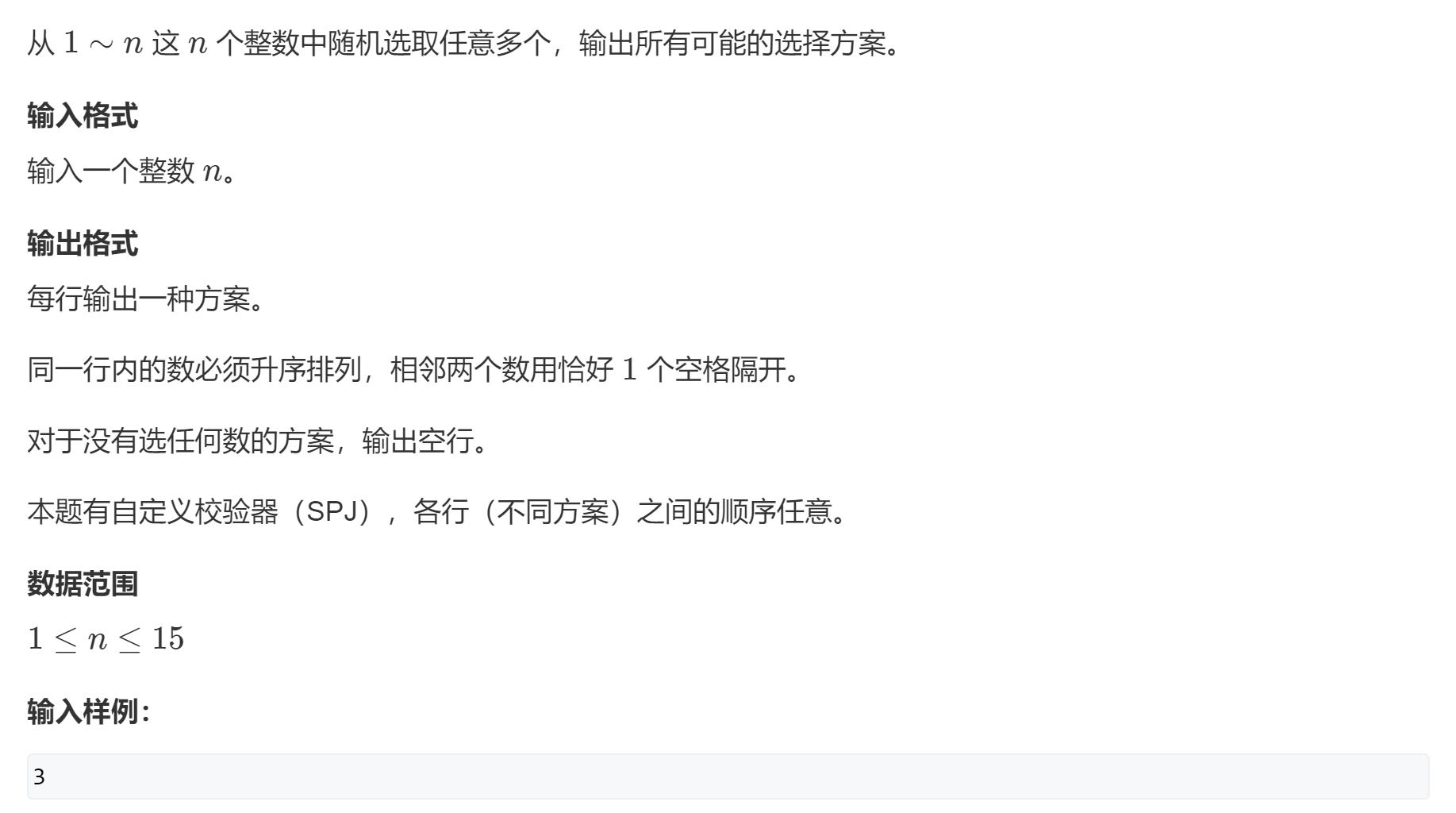
首先复习数据范围,n是小于15的,符合n<=30的条件,所以可以使用n*n!的dfs(递归)
输出样例:
3
2
2 3
1
1 3
1 2
1 2 3
分析这个题:
如果n = 3,那么将会从3个中选取任意数量的个数来进行输出,如果要保证最终的输出不会有情况忽略,那么就需要保证顺序(从第一位开始分情况讨论,然后以此类推第二位,第三位)边界就是第三位填完了,这里如果到达边界可以不用返回,只需要输出就可以,所以在’return;‘之前输出一下即可。
因为需要判断以及控制这三位,所以需要将这三位调成可以控制的形式:数组。
代码实现
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N = 16;//设置最大的数组长度,可以不用到这么大的范围,但是必须有。
int n;
int st[N];//数组状态(对应数的状态):0表示还没有考虑,1表示选他,2表示不选他
void dfs(int u)
{
//首先先确定边界情况
if(u>n)//如果传进来的要控制的位u是大于n的,那么就是边界外了,进应该进行输出了。
{
for(int i = 0;i<=n;i++)//将n位上的标志是1的全部输出
{
if(st[i]==1)
{
printf("%d ",i);
}
}
printf("\n");
return ;
}
//然后就处理分支——处于递归搜索树的某个结点上,这个时候有两种情况要选择:选它或者不选它不选它
st[u] = 2;//直接将它的状态改成:不选
dfs(u+1);//然后处理它(不选)的情况(分支1)即可,调用递归
st[u] = 0;//最后恢复现场
st[u] = 1;//选
dfs(u+1);//处理它(选)的情况(分支2),调用递归
st[u] = 0;//最后恢复现场
}
int main()
{
cin>>n;
dfs(1);//下标从1开始
return 0;
}
注意:如果在分情况讨论的时候对父结点进行赋值/改变,那么必须要进行恢复(不能因为分子情况而影响了自己)。
再写一遍:
#include<iostream>
using namespace std;
#include<string>
#include<iomanip>
int st[16];
int n = 0;//需要创建全局变量,因为n在外面的函数中需要用到
void dfs(int u)//必须是最后一个(第三位)确定了以后再打印
{
if (u > n)
{
for (int i = 1; i <= n; i++)
{
if (st[i] == 1)
{
printf("%d ", i);
}
}
printf("\n");
return;//不要忘了一种情况(方式)打印完需要return回来。
}
st[u] = 2;
dfs(u + 1);
st[u] = 0;
st[u] = 1;
dfs(u + 1);
st[u] = 0;
}
int main()
{
cin >> n;
dfs(1);
return 0;
}
界限是需要考虑的,这里虽然是有界限的,而且在一开始构思代码的时候就应该想到界限是怎么触到的。
上面的方法是将方案直接输出,如果想把所有的方案都记录下来,然后再统一输出,那么就需要使用二维数组。(如果要先记录下来的话,那么肯定是等到所有的位上都有确切的值了以后,一齐放进数组中,这算一种方式,最多有2的n次方种方式。但是在设计数组的时候需要按照最多情况来设计。)
#include<iostream>
using namespace std;
#include<string>
#include<iomanip>
int n = 0;
int num = 1;//方式的序号
int st[16];
int arr[1 << 15][16];
void dfs(int u)
{
if (u > n)
{
for (int i = 1; i <= n; i++)//在边界处记录方案到二维数组中
{
if (st[i] == 1)
{
arr[num][i] = i;
}
}
num++;
return;
}
st[u] = 1;
dfs(u + 1);
st[u] = 0;
st[u] = 2;
dfs(u + 1);
st[u] = 0;
}
int main()
{
cin >> n;
dfs(1);
for (int i = 1; i <=num; i++)
{
for (int j = 1; j <= n; j++)
{
if(arr[i][j]!=0)
printf("%d ", arr[i][j]);
}
if(i!=num)
printf("\n");
//puts("");//输出一个字符串加回车,字符串为空的时候相当于回车。
}
return 0;
}
最后不知道怎么回事,多回车了一行,消除了这一行就正确了。(注意,如果我没有进行特殊判断的话,那么打印出来的方案都是三位的,即使没有,那么最终答案也是0,所以我使用了特殊判断,只要是0就不输出,也可以使用vector,但是我不会用)
上面的数组中的数如果不是1 的话就不需要打印了,所以直接判断是不是1即可,如果需要全排列的话,每个数都是需要涉及的,所以需要判断每个数,也就是说要将1-n分别判断一遍,即对数字进行判断,而不是对数组的值进行判断(需要一个used数组来判断这个数有没有被用过)。下面的arr数组中的值也不再是1,2,3这样的状态,而是10个不同的数的状态,0表示还没有数,1-9表示有数了。
递归实现(排列型)枚举
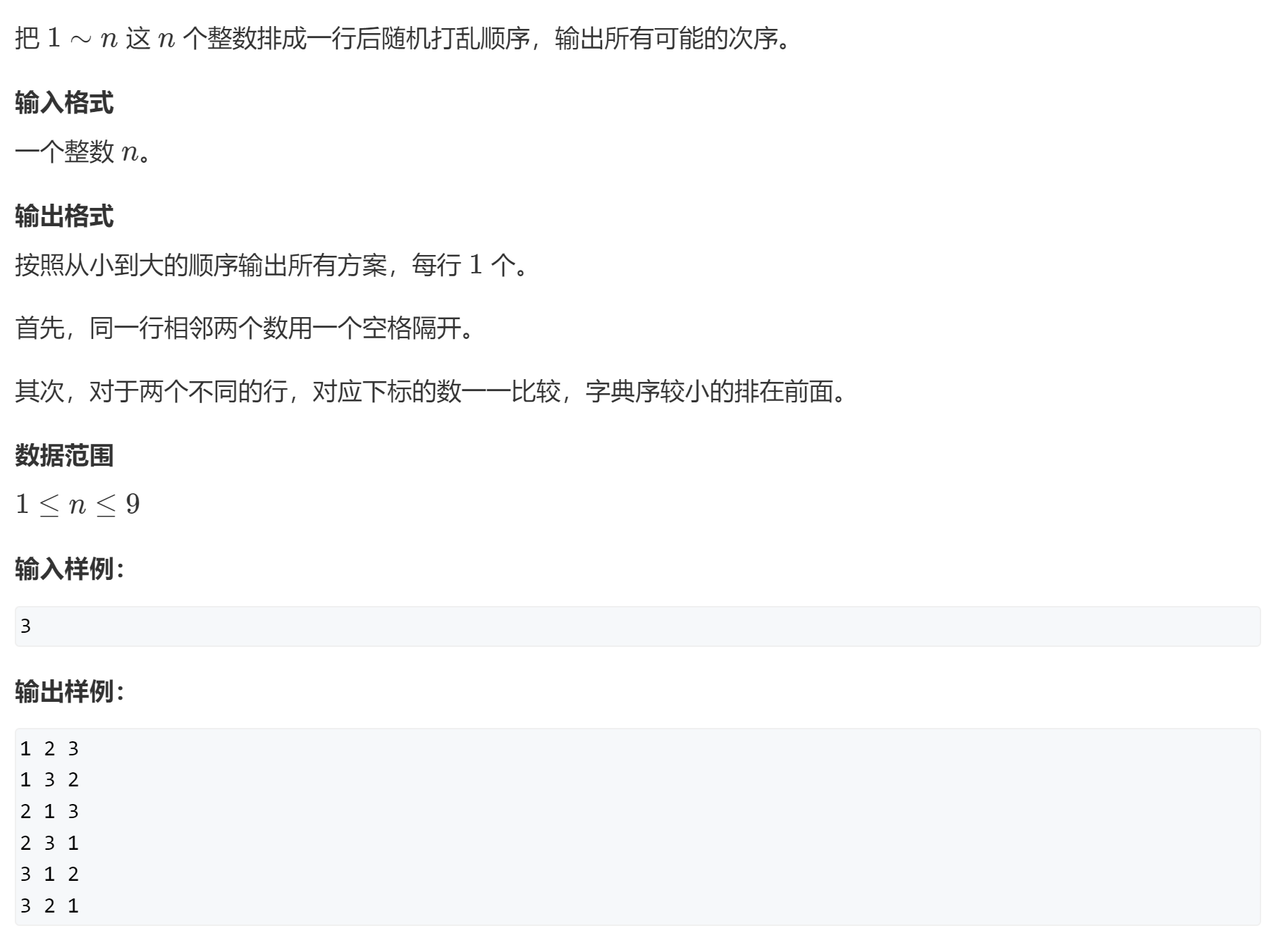
看到数据范围,n<=9,满足n<=30,所以可以考虑dfs递归。(n*n!)
这个题的意思就是输出n 的全排列。
字典序:
有两个序列a,b进行比较大小,如果a1 = b1,那么就继续向后进行比较,直到ai!=bi。如果到最后都相等,那么两个序列相同,如果ai存在而bi不存在,那么说明bi小于ai。(出题人比较懒,他没有将每种符合题意的情况都考虑到并加上,所以方案唯一)(只要按照正常规律去写,就不用在意这个字典序,因为正常来说都是先枚举1,然后依次向后。搜索递归树中,左边的分支肯定是比右边的分支大的)
一般全排列有两种枚举方式
第一种是依次枚举每个数放到哪一个位置。(先放1,再放2,依次放最后一个)
第二种是依次枚举每个位置放哪一个数。(第一个位置放3,第二个位置放2,以此类推)
每个数只能用一次,所以需要判断一下每个数值只用一次。(所以需要判断当前这个位置可以用的数有哪些)需要存一个新的状态,用来表示每个数是不是被用过。
按照第二种方法来实现代码
#include<iostream>
using namespace std;
#include<string>
#include<iomanip>
int st[10];//0表示还没有放数,1-n表示放了数了。
int n;
bool used[10];//用来判断数是否被用过,true表示用过了。
void dfs(int u)
{
if (u > n)
{
for (int i = 1; i <= n; i++)//打印方案
{
printf("%d ", st[i]);
}
puts("");
return;
}
//枚举每个分支,即当前的位置可以填那些数。
for (int i = 1; i <= n; i++)//目标是一个位置,而讨论的是放那个数进去。
{
if (!used[i])//如果这个数没有用过
{
st[u] = i;
used[i] = true;
dfs(u + 1);
//恢复现场
st[u] = 0;
used[i] = false;
}
}
}
int main()
{
cin >> n;
dfs(1);
return 0;
}
分析这个全排列算法的时间复杂度:
这个算法会递归n层
第一层是n,(,就一个for循环,所有的数都可以选)
第二层是n*n,(有n个分支,每个分支中都有一个for循环)
第三层是n*(n-1) *n,(有n * (n-1)个分支,每个分支中都有一个for循环)
等到了叶子结点,就会有n!个分支,然后每个分支中有个for循环(输出的时候需要将n个位置上的数遍历一遍),所以,最后的时间复杂度就是n*n!
总共的时间复杂度是n*(1 + n + n * (n-1)+ n* (n-1)(n-2)…+n!)
经过放缩就是n*n!。
递归实现(组合型)枚举
组合型与排列型的区别:
排列型是注重的顺序的,比如132和123就是不同的两个方案。
组合型是不注重顺序的,比如132和123是相同的两个方案。
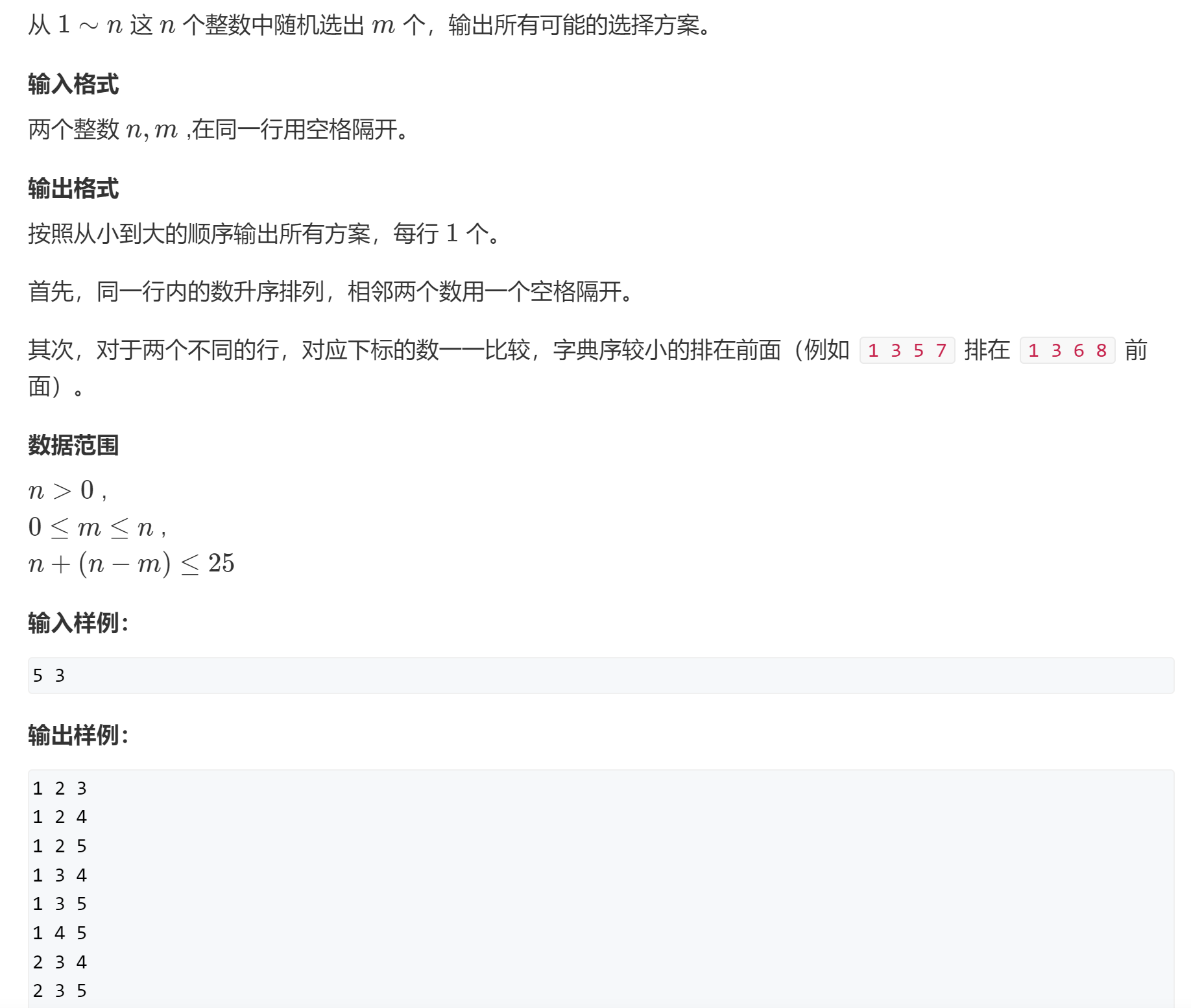
这里要求组合型枚举,那么就需要解决132,123,321等重复的问题,要求只能存在一个。
解决方法:人工规定一个枚举顺序,比如要求只有123这样按照从小到大这样的枚举顺序排列才是正确的,才会被打印。在递归的时候加一个限制,保证从小到大的顺序(局部属性,只需要保证新加的数是大于前一个数的)。
然后根据递归搜索树来写代码:
首先确定参数:
1,三个空位的状态时需要的,开一个长度为n的数组来记录。
2,当前在枚举中的哪个位置,传一个变量就可以了。(u)
3,后面位置的取值范围,要保证升序(需要传一个最小数start作为开始,也就是前一个数)
ps:发现这个组合型枚举的结果是可以用指数型枚举中的代码实现的,只需要挑出符合长度的数值。
代码实现:
#include<iostream>
#include<string>
using namespace std;
const int N = 30;
int n, m;
int way[N];//每个位置的状态,(数)。0表示空,如果用完了就需要把它恢复成空。
void dfs(int u,int start)//当前位置和开始位置
{
//先想一下边界
if (u > m)//u=1的时候一个数也没有选,u=2的时候就相当于选了1个数了。
{
for (int i = 1; i <=m; i++)
{
printf("%d ", way[i]);
}
puts("");
return;
}
for (int i = start; i <= n; i++)
{
way[u] = i;
dfs(u + 1, i + 1);
way[u] = 0;
}
}
int main()
{
scanf("%d%d", &n, &m);
dfs(1, 1);
return 0;
}
补充:DFS的优化—剪枝
以上面的组合型代码为例子,假设当前正在选第u个数,那么就代表已经选了(u-1)个数,将从start开始到n结束的数按顺序放到数组dt[N]中,如果从start开始到n结束中间的数的数目过小,导致这个数加上u-1是小于m的(选不全),那么就可以直接return了。
即n-start+1+u-1 = n+u-start<m 的情况下就可以直接return。(相当于边界)
如果把后面所有数都选上,都不够m个,当前分支一定无解。
#include<iostream>
#include<string>
using namespace std;
const int N = 30;//多给一点防止越界
int dt[N];
int n, m;
void dfs(int u,int start)
{
if (n + u - start < m) return;//剪枝
if (u > m)
{
for (int i = 1; i <=m; i++)
{
printf("%d ", dt[i]);
}
puts("");
return;
}
for (int i = start; i <= n; i++)//开始选数放进去了,从start开始,到n结束。
{
dt[u] = i;
dfs(u + 1, i + 1);//注意start代表最开始的位置,是不能改变的,改变的是代表开始位置的i。
dt[u] = 0;
}
}
int main()
{
scanf("%d%d", &n, &m);
dfs(1, 1);
return 0;
}
优化完时间快了三倍。