一、损失函数

损失函数是用来评价预测值和真实值的不一致程度，，损失函数越好，通常模型的性能越好。
常用的损失函数：最小均方差
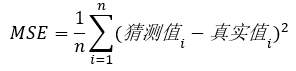
在这里插入图片描述

最好的均方差MSE是无限接近于0(图像的导数等于0)。

二、梯度下降

1、到底什么是梯度下降？

简单理解： 假如你在山顶，你想以以最快的方式下山，最好的办法就是顺着坡度最陡峭的地方走下去。由于不熟悉路，下山的过程每走过一段路程就需要停下来观望，从而选择最陡峭的下山路。这样就可以在最短的时间内下山。
梯度下降原理：在下降一个梯度的阶层后，寻找一个当前获得的最大坡度继续下降。

2、学习速率

简单来讲，还是前面的那个例子，学习速率就是在你下山时候的步长。
在下山的时候，初期你下山的步长会很大，快到山底的时候你的步长就会减少。
即：最理想的学习率不是固定值, 而是一个随着训练次数衰减的变化的值, 也就是在训练初期, 学习率比较大, 随着训练的进行, 学习率不断减小, 直到模型收敛(趋近于一个数即倒导数等于0).

三、梯度下降使用数学解决

假设回归函数为一次函数：y=mx+b
y=mx+b即为猜测值
1、首先找到MSE变化最缓慢的地方，即导数接近于0的地方
对MSE求偏导，分别对m、b求一次导。
在这里插入图片描述
假设初始时 m=1 b=1，
每次变化m b的值即迭代

学习速率为0.00001时：
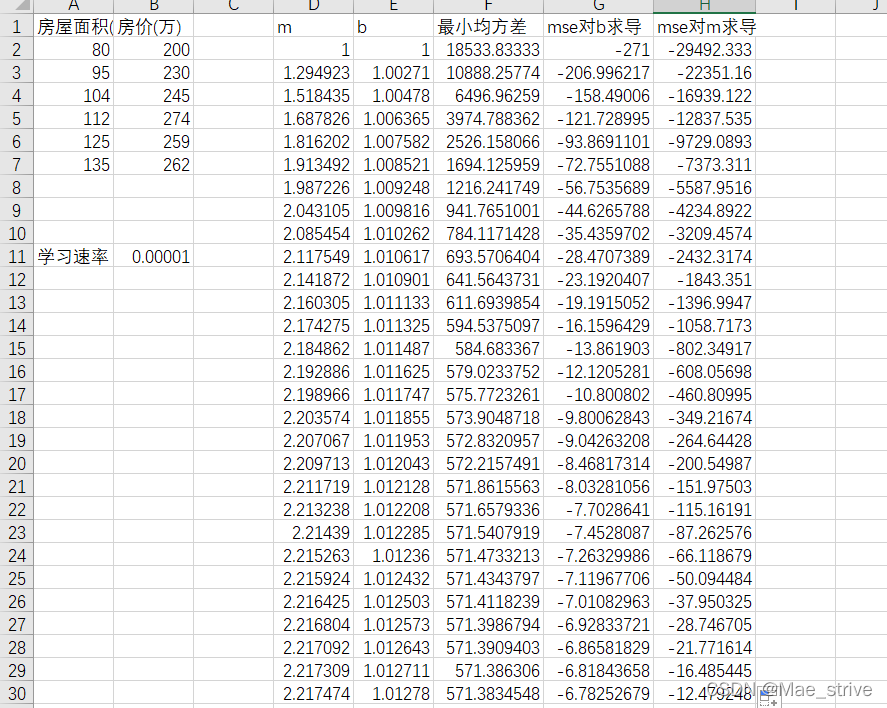
在这里插入图片描述

可以看到m接近0时 b还是-6多要继续迭代，直到 m b都接近于0（大约要100多万次）。
我们的EXCEL表格的列数远远达不到。

四、使用代码实现梯度下降

函数设计：

grandientdecent():运行一次梯度下降算法
train():多次运行梯度下降算法
predict():使用train()对m和b进行预测
test():测试预测的准确性，模型评估

import numpy as np
import datetime

data = np.array([
    [80, 200],
    [95, 230],
    [104, 245],
    [112, 274],
    [125, 259],
    [135, 262]
])
m = 1
b = 1

xarray = data[:, 0]
yarray = data[:, -1]
lr = 0.00001


def grandientdecent():
    # b的斜率
    bslop = 0
    for index, x in enumerate(xarray):
        bslop += m * x + b - yarray[index]
    bslop = bslop * 2 / len(xarray)
   # print("mse对b求导={}".format(bslop))
    # m的斜率
    mslop = 0
    for index, x in enumerate(xarray):
        mslop += (m * x + b - yarray[index]) * x
    mslop = mslop * 2 / len(xarray)
   # print("mse对m求导={}".format(mslop))
    return (bslop, mslop)


def train():
    for i in range(1, 1000000):
        bslop, mslop = grandientdecent()
        global m
        m = m - mslop * lr
        global b
        b = b - bslop * lr
        if (abs(mslop) < 0.5 and abs(bslop) < 0.5):
            break
    end_time = datetime.datetime.now()
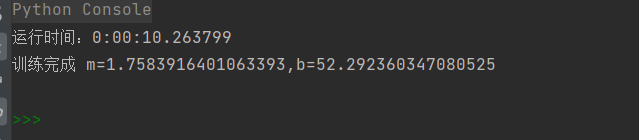
    print("运行时间：{}".format(end_time - start_time))
    print("训练完成 m={},b={}".format(m, b))


if __name__ == "__main__":
    start_time = datetime.datetime.now()
    train()