https://leetcode-cn.com/problems/all-oone-data-structure/
请你设计一个用于存储字符串计数的数据结构,并能够返回计数最小和最大的字符串。
实现 AllOne 类:
- AllOne() 初始化数据结构的对象。
- inc(String key) 字符串 key 的计数增加 1 。如果数据结构中尚不存在 key ,那么插入计数为 1 的 key 。
- dec(String key) 字符串 key 的计数减少 1 。如果 key 的计数在减少后为 0 ,那么需要将这个 key 从数据结构中删除。测试用例保证:在减少计数前,key 存在于数据结构中。
- getMaxKey() 返回任意一个计数最大的字符串。如果没有元素存在,返回一个空字符串 “” 。
- getMinKey() 返回任意一个计数最小的字符串。如果没有元素存在,返回一个空字符串 “” 。
示例:
输入
["AllOne", "inc", "inc", "getMaxKey", "getMinKey", "inc", "getMaxKey", "getMinKey"]
[[], ["hello"], ["hello"], [], [], ["leet"], [], []]
输出
[null, null, null, "hello", "hello", null, "hello", "leet"]
解释
AllOne allOne = new AllOne();
allOne.inc("hello");
allOne.inc("hello");
allOne.getMaxKey(); // 返回 "hello"
allOne.getMinKey(); // 返回 "hello"
allOne.inc("leet");
allOne.getMaxKey(); // 返回 "hello"
allOne.getMinKey(); // 返回 "leet"
提示:
- 1 <= key.length <= 10
- key 由小写英文字母组成
- 测试用例保证:在每次调用 dec 时,数据结构中总存在 key
- 最多调用 inc、dec、getMaxKey 和 getMinKey 方法 5 * 104 次
思路:
- 数据结构1:保存每个key及其出现的次数。按序排列
- 数据结构2:优化查找key的速度,取消遍历数据结构1匹配key的过程。
基于以上思路,
数据结构1选取双向链表,因为随着inc操作,链表中的结点位置会频繁变动需要具备增删改操作都是O(1),且结构本身需要具备有序。
数据结构2选取哈希map,因为hash增删改查操作都是O(1)。
因此,我们可采用以下结构(错误示范,不满足时间复杂度O(1)):
// 双向链表,每个节点存放 key 及其出现次数。以计数递增排列
list<pair<string, int> > lst;
// 哈希表存放 字符串对应的结点位置(在lst中的位置)
unordered_map<string, list<pair<string, int> >::iterator > nodes;
按照上述结构,inc操作的伪代码如下:
inc操作:
如果key已经存在:计数+1
维护链表递增
如果key不存在:
添加新的key到lst与nodes中。
关键点在于如何维护链表递增:
循环执行:
当前计数 > 后一个key的计数: 交换位置
但是对于上述操作,有一种用例不满足题目要求。例如:当所有key在list中出现的次数相同时,此时再进行inc操作时,可能会有O(n)的时间复杂度。
示例:所有元素的计数值都为4,此时inc操作后,aaa的计数值为5 。 此时在维护链表有序时需要进行n次匹配。
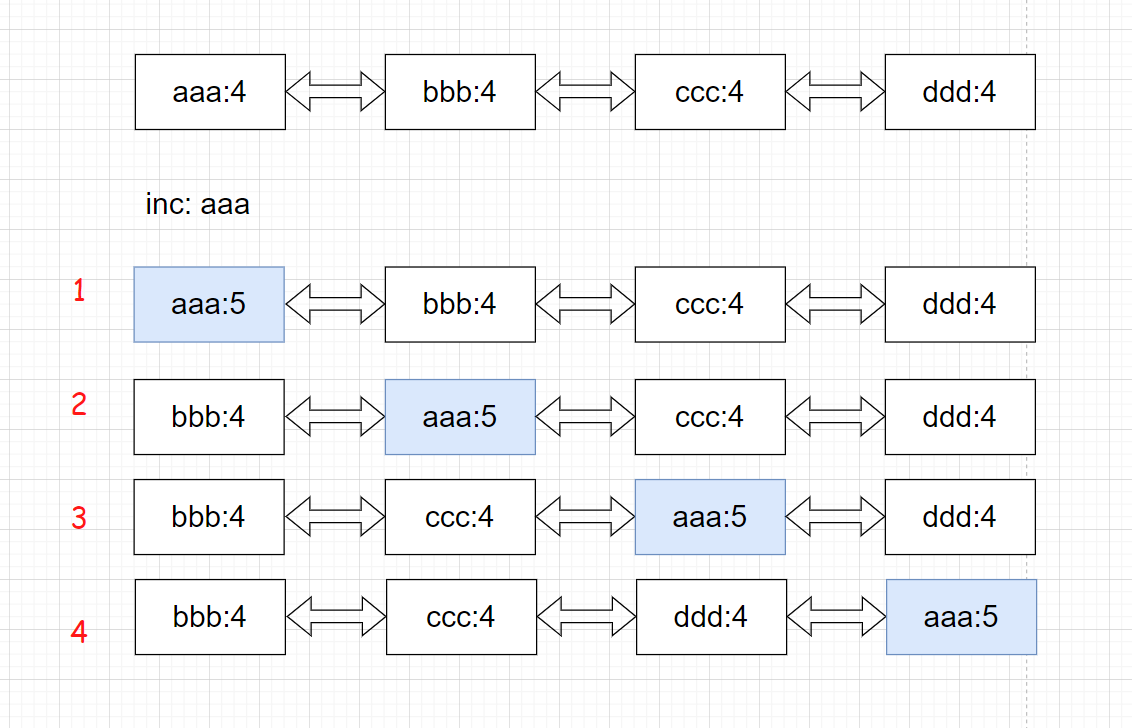
因此,我们需要重新定义数据结构。
可以发现,当部分key的计数值一样时,我们需要维护链表有序时需要重复的进行比较与交换。而如果我们将重复的元素看做一个整体,那么维护链表有序就变得容易了。
示例:当我们inc:ttt时。只需要与后一个集合比较,如果相同则归为下一个集合中。
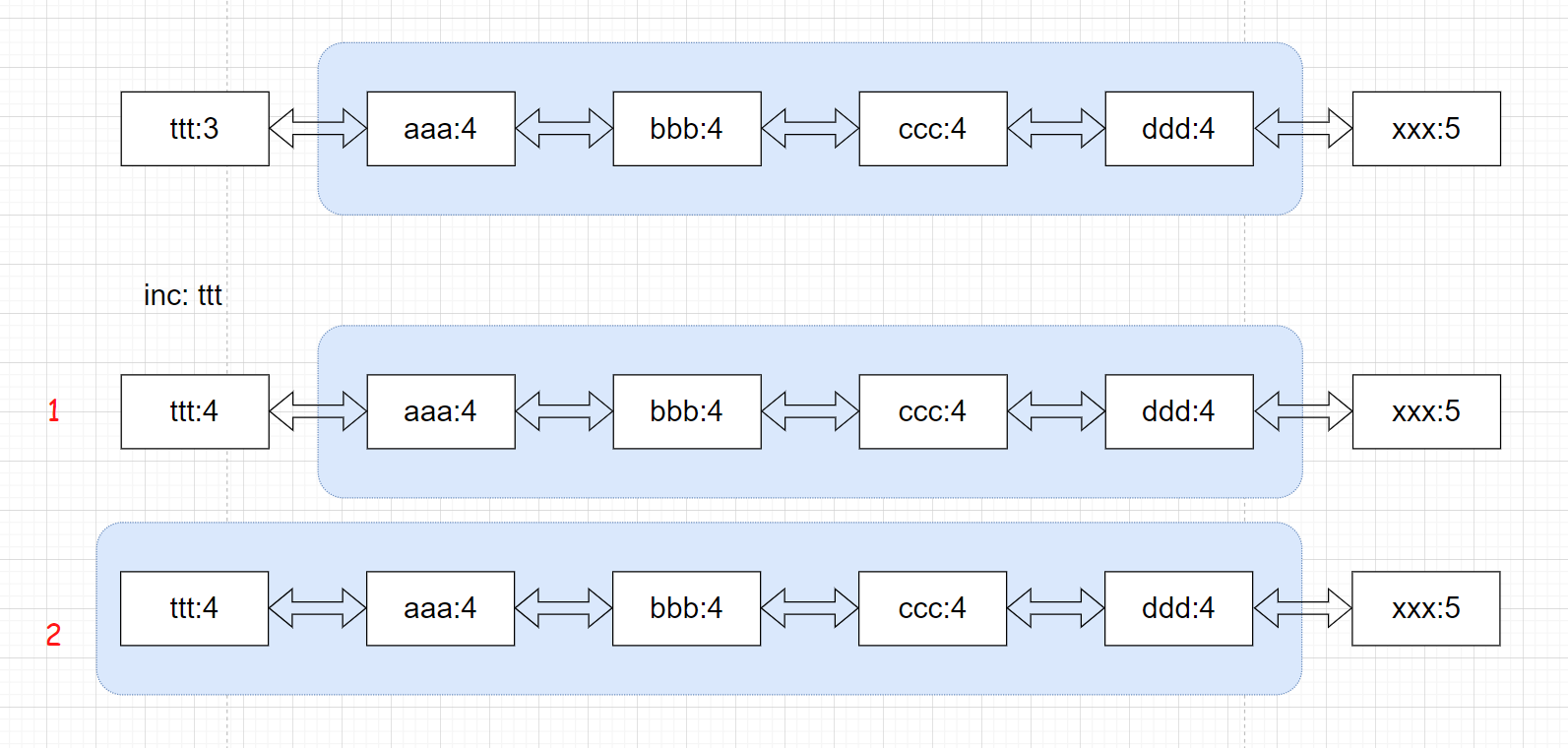
如果没有相同计数的集合,则新建一个集合(删除旧集合)
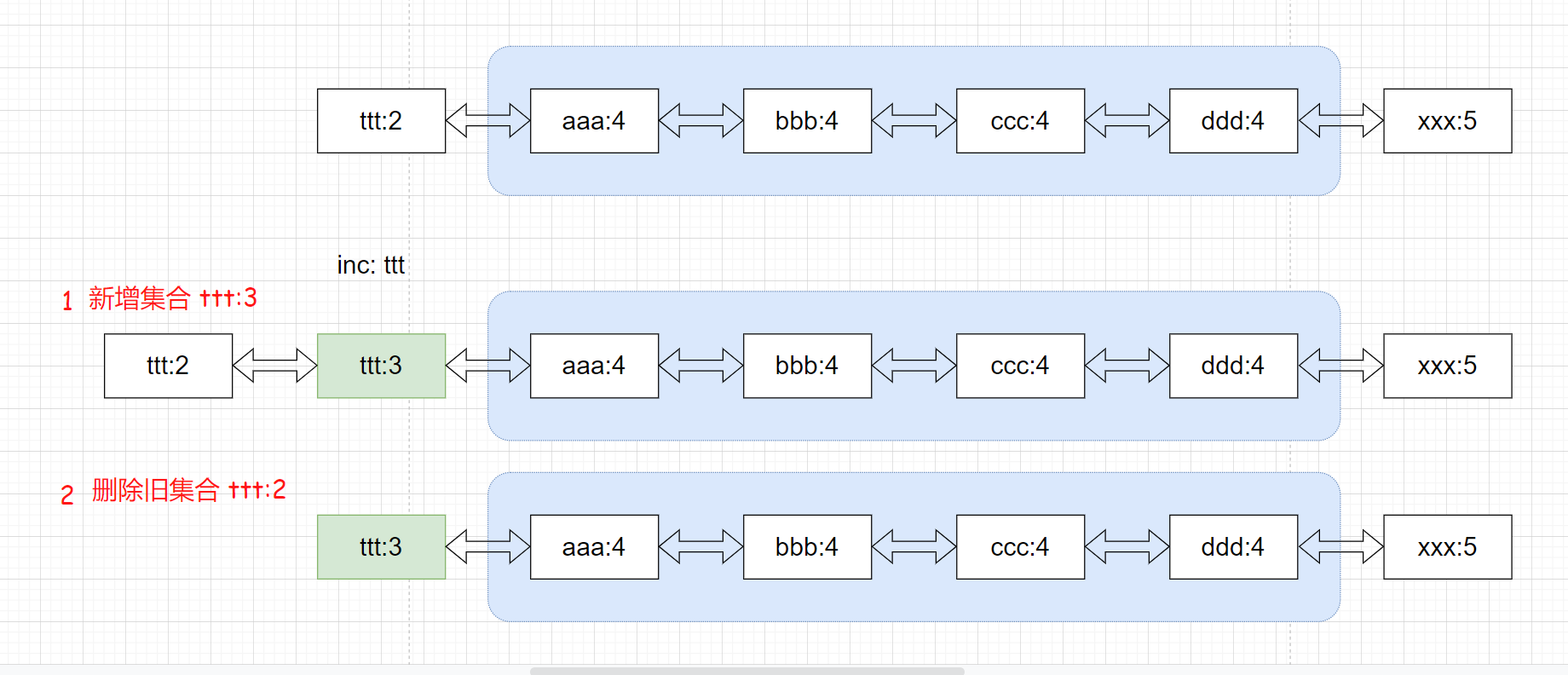
如果计数大于当前集合,则直接跳至下一集合(删除旧集合)
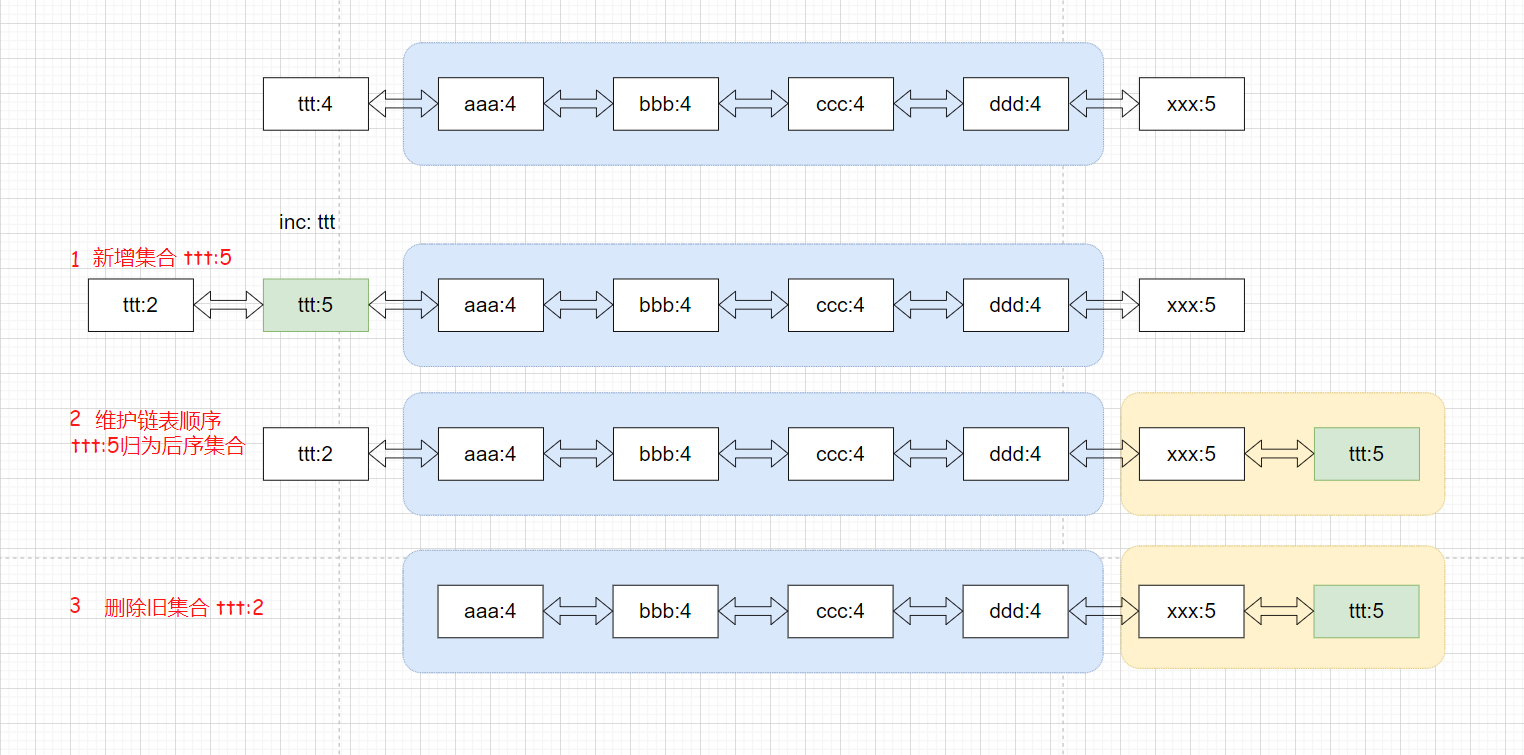
按照以上规则,我们只需要修改lst链表的结点即可。
数据结构定义:
// 双向链表,每个节点存放,出现相同次数的key的集合,按照计数递增的顺排列
list<pair<unordered_set<string>, int> > lst;
// 哈希表存放 相同计数的字符串集合 在lst中对应的结点位置
unordered_map<string, list<pair<unordered_set<string>, int> >::iterator > nodes;
结构示意:

代码参考官方题解;C++版
class AllOne {
// 链表:结点first存放集合,second存放计数值
list<pair<unordered_set<string>, int>> lst;
// 哈希map:键:输入的关键字,值:关键字在链表中的位置
unordered_map<string, list<pair<unordered_set<string>, int>>::iterator> nodes;
public:
AllOne() {}
void inc(string key) {
if (nodes.count(key)) { // key是否出现过
// 找到key存放在list中的结点 cur, 后继结点 nxt
auto cur = nodes[key], nxt = next(cur);
/* 是否需要新增集合:两种情况
** nxt == lst.end():当前结点是list的尾结点,则当前结点计数加一后(最大计数),需要新增一个集合保存最新的计数值
** nxt->second > cur->second + 1: 当前结点计数值加一后,不足以加入下一集合。需要诞生一个新的集合容纳最新计数值。
** 例如当前集合计数为 2, 下一集合计数为4, 当前key计数加一后需要一个计数为3的集合。*/
if (nxt == lst.end() || nxt->second > cur->second + 1) {
unordered_set<string> s({key}); // 新增集合
nodes[key] = lst.emplace(nxt, s, cur->second + 1); // 在当前位置插入新集合与新计数值
} else { // 不需要新增集合,直接加入下一集合
nxt->first.emplace(key); // 将key移动到后继结点所在的集合中
nodes[key] = nxt; // 更新nodes。key与lst的位置关系
}
cur->first.erase(key); // 从旧集合中删掉key(因为,kay已经加入新集合中了)
if (cur->first.empty()) { // 如果,旧集合空了,从lst中删除旧集合
lst.erase(cur);
}
} else { // key 不在链表中
/* 从链表头部插入的情况:即头部没有计数值为1的结点,两种情况:
** 链表为空
** 链表首结点计数大于1 */
if (lst.empty() || lst.begin()->second > 1) {
unordered_set<string> s({key});
lst.emplace_front(s, 1); // 链表头部插入{集合,1}
} else { // 正常插入,链表首结点有计数值为1的结点,插入到该位置即可
lst.begin()->first.emplace(key);
}
// 将key对应的位置,保存到nodes中,便于查找
nodes[key] = lst.begin();
}
}
void dec(string key) {
// 找到key对应的结点(集合所在位置)
auto cur = nodes[key];
if (cur->second == 1) { // key 仅出现一次,将其移出 nodes
nodes.erase(key);
} else { // key 出现多次,不能直接删除,需要移动
// 找到前驱。key计数减一后移动至前驱所在集合
auto pre = prev(cur);
/* 需要新增前驱结点:两种情况
** 当前在key在首结点位置,计数值减一后没有现成的集合
** 当前key的前驱结点,不足以容纳key减一后的计数值 **/
if (cur == lst.begin() || pre->second < cur->second - 1) {
unordered_set<string> s({key}); // 新增结合
nodes[key] = lst.emplace(cur, s, cur->second - 1); // 插入cur的前驱位置
} else { // 不需要新增结点,前驱可以容纳key计数减一
pre->first.emplace(key); // 将key加入前驱结点
nodes[key] = pre; // 跟新nodes。key与lst的位置关系
}
}
cur->first.erase(key); // 从当前集合中移除key,因为key已经移动到前驱结点所在集合了
if (cur->first.empty()) { // 如果当前集合空了,删除集合所在结点
lst.erase(cur);
}
}
string getMaxKey() { // lst尾结点是计数值最大的
return lst.empty() ? "" : *lst.rbegin()->first.begin();
}
string getMinKey() { // lst首结点是计数值最小的
return lst.empty() ? "" : *lst.begin()->first.begin();
}
};