[数据结构与算法]平衡二叉树旋转原理【超详细解读】

1. 理解前的知识储备

• 二叉排序树

  通常二叉排序树呈现的特点是左子树元素值<根节点值<右子树元素值

  即右子树元素全部大于左子树元素及根节点；左子树元素全部小于右子树元素及根节点

• 平衡二叉树

  左右子树高度差小于等于1的二叉排序树

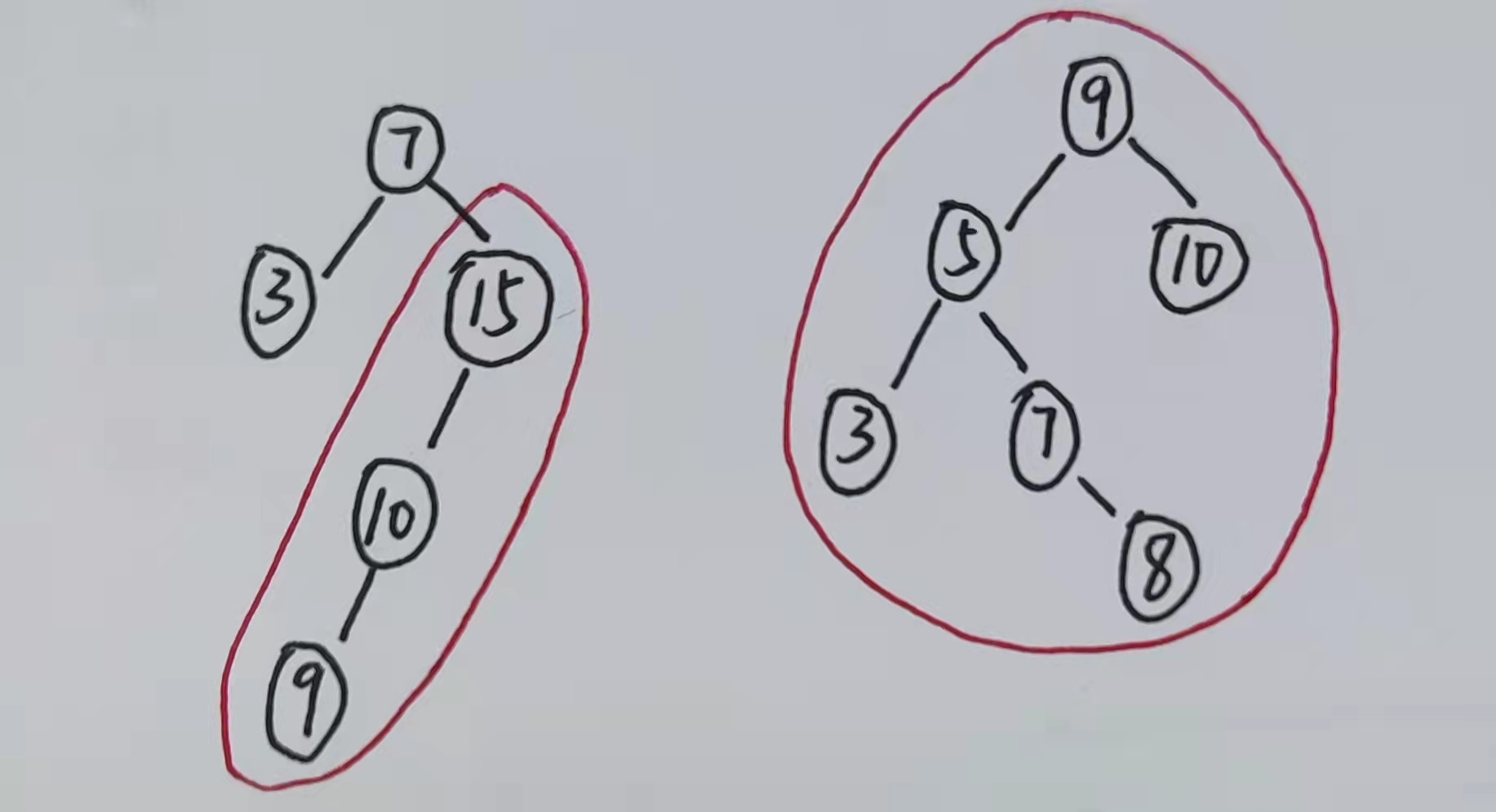
• 最小不平衡树

  一棵二叉排序树中左右子树高度差大于1的最小单位树。平衡二叉树插入新节点后只可能出现一棵最小不平衡树，经过平衡调整后的平衡二叉树不存在最小不平衡树

  以下是两个例子，红笔圈起来的部分即最小不平衡树

  

2.LL旋转

当新节点添加在最小不平衡树根节点的左孩子的左子树且造成不平衡时使用此旋转

操作

1. 确定最小不平衡树在整棵树中的位置

2. 定位到此树根节点R的左节点P，目标是让P成为最终的根节点

3. 将左节点P进行右旋转【即让P去到根节点R的位置，根节点R下沉到右节点】，此操作不会破坏二叉排序树的结构

4. 若左节点P有右子树，则一并放到旋转后的根节点R的左边

   这里用到了二叉排序树右子树大于左子树的性质，因为原先P的右子树属于根节点R的左子树，所以P的右子树中所有节点值必定小于根节点R以及根节点R的右子树。

   经过旋转后，根节点R成为了P的右子树，而原先P的右子树必然是比P大且小于根节点R的，所以原先P的右子树放在P的右边，根节点R的左边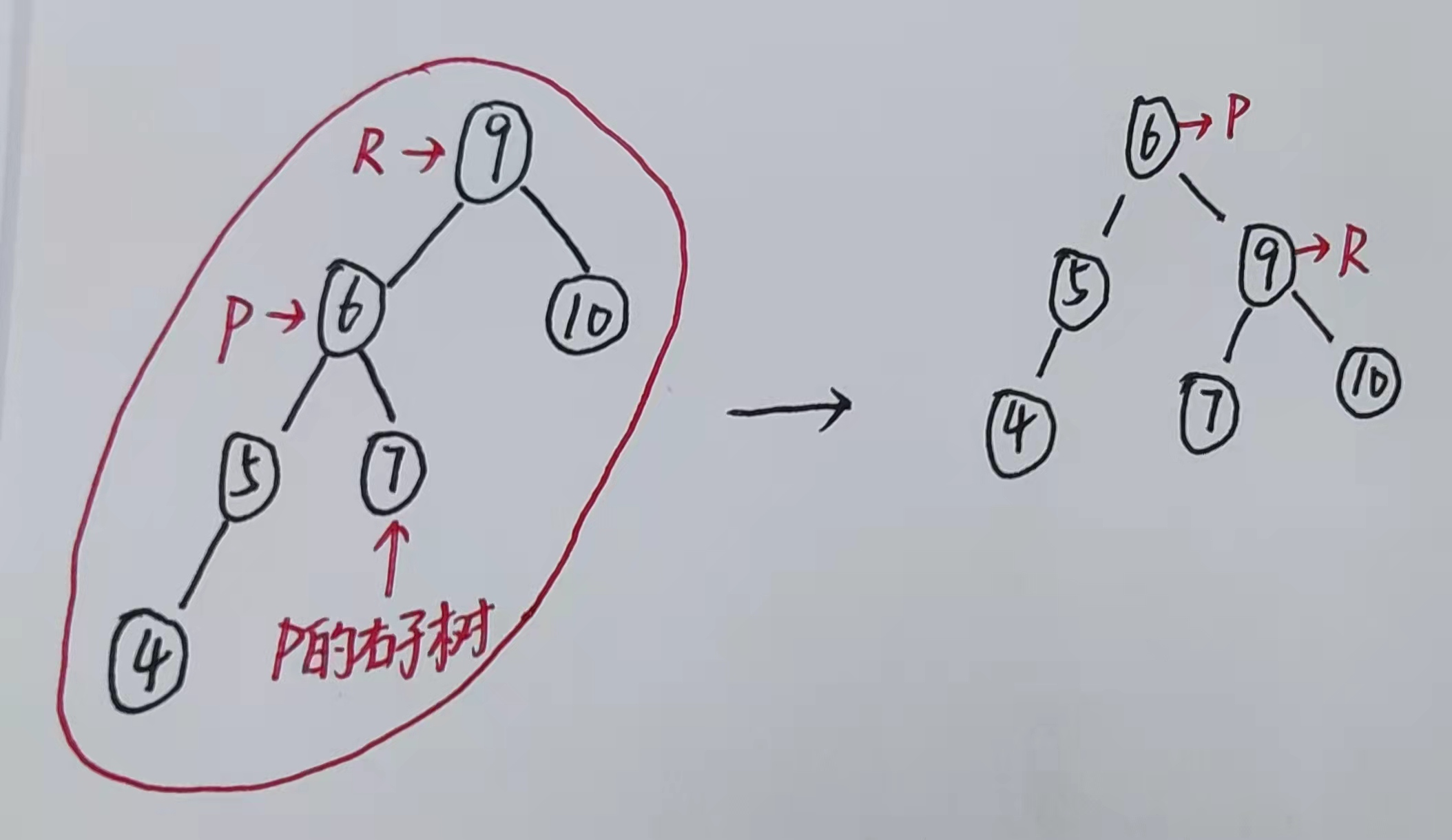

   

3.RR旋转

当新节点添加在最小不平衡树根节点的右孩子的右子树且造成不平衡时使用此旋转

操作

1. 确定最小不平衡树在整棵树中的位置

2. 定位到此树根节点R的右节点P，目标是让P成为最终的根节点

3. 将右节点P进行左旋转【即让P去到根节点R的位置，根节点R下沉到左节点】，此操作不会破坏二叉排序树的结构

4. 若右节点P有左子树，则一并放到旋转后的根节点R的右边

   这里用到了二叉排序树左子树小于右子树的性质，因为原先P的左子树属于根节点R的右子树，所以P的左子树中所有节点值必定大于根节点R以及根节点R的左子树。

   经过旋转后，根节点R成为了P的左子树，而原先P的左子树必然是比P小且大于根节点R的，所以原先P的左子树放在P的左边，根节点R的右边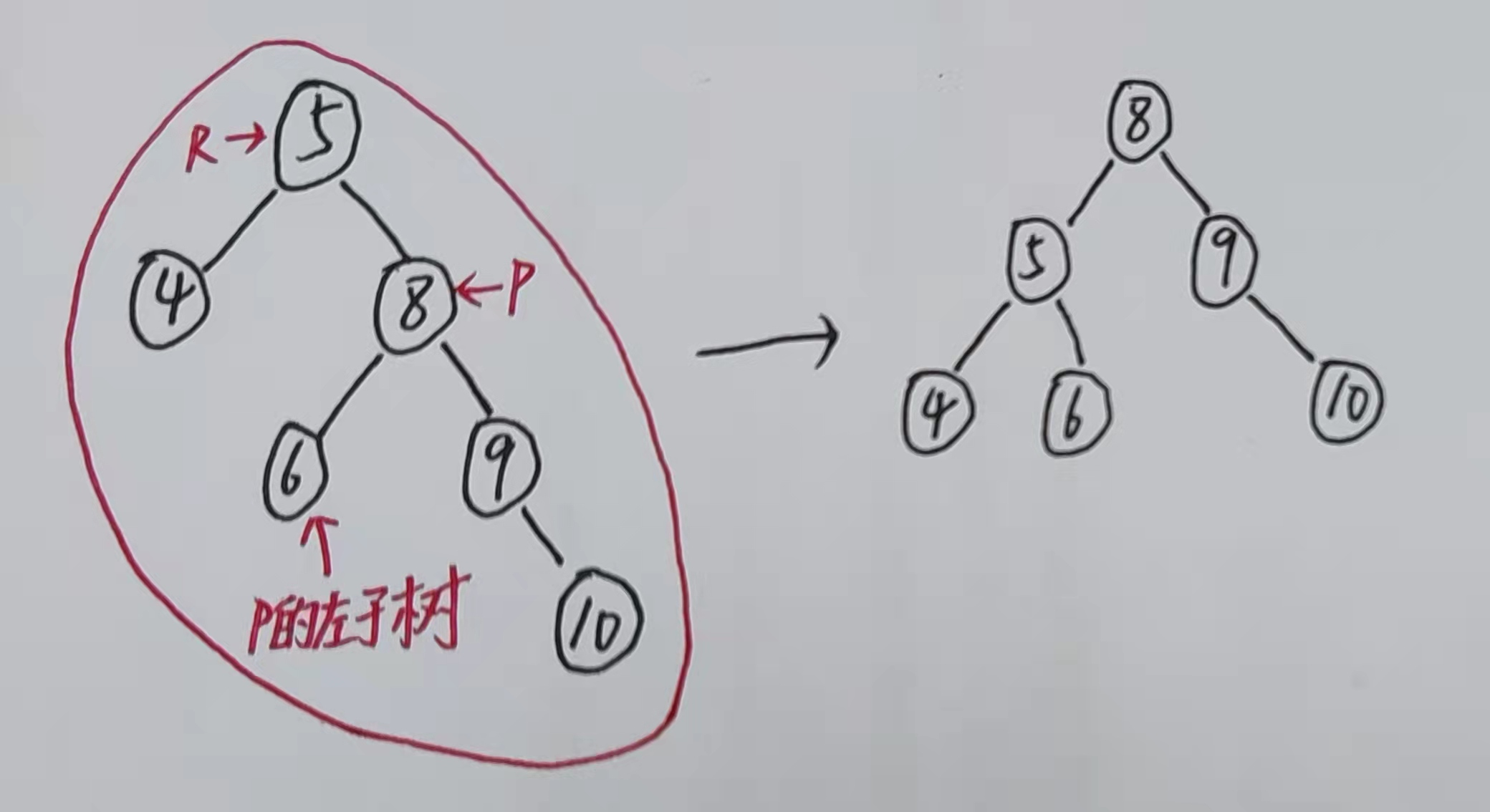

   

4.LR旋转

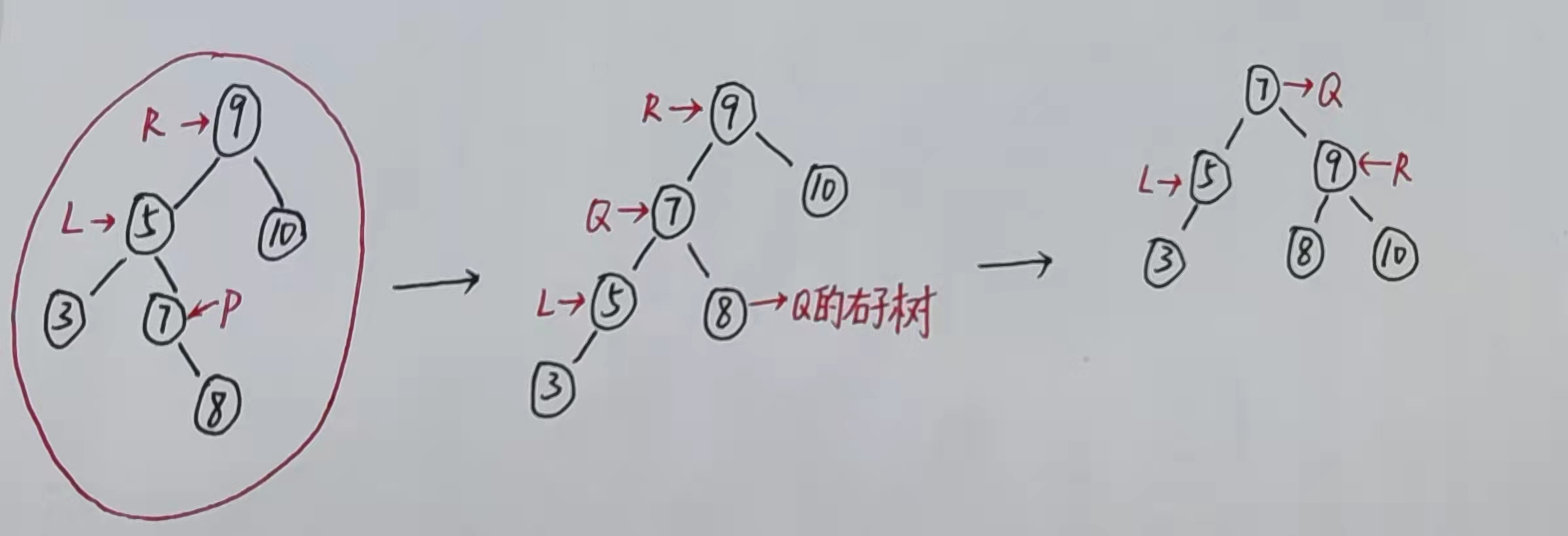
当新节点添加在最小不平衡树根节点的左孩子的右子树且造成不平衡时使用此旋转

操作

1. 确定最小不平衡树在整棵树中的位置

2. 定位到此树根节点R的左节点L的右孩子P，目标是让P成为最终的根节点

3. 先将P左旋转到L的位置，此时将P记作Q

4. 再将Q右旋转到R的位置

5. 同理，若Q有右子树，则将此右子树一并放入到旋转后根节点R的左边

   原理同LL与RR旋转，可仔细体会上述解释过程

   

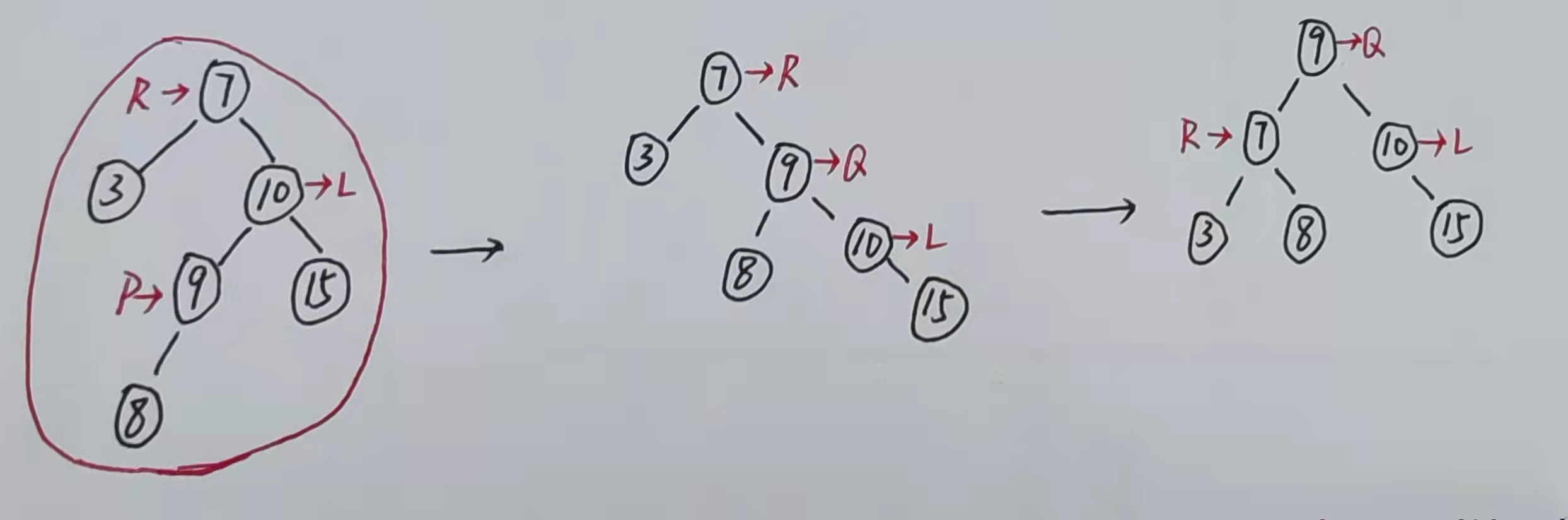
5. RL旋转

当新节点添加在最小不平衡树根节点的右孩子的左子树且造成不平衡时使用此旋转

操作

1. 确定最小不平衡树在整棵树中的位置

2. 定位到此树根节点R的右节点L的左孩子P，目标是让P成为最终的根节点

3. 先将P右旋转到L的位置，此时将P记作Q

4. 再将Q左旋转到R的位置

5. 同理，若Q有左子树，则将此左子树一并放入到旋转后根节点R的右边

   原理同LL与RR旋转，可仔细体会上述解释过程

6. 总结

平衡二叉树的旋转不需要死记，千万不要被通篇的左右子树给弄迷糊了，建议可以画图进行步骤阅读，结合二叉排序树的性质可以更好的进行理解，若这篇文章对你有所帮助的话，不放给个免费的赞支持一下。