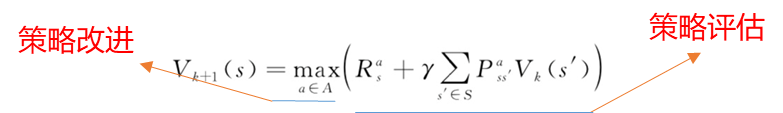[数据结构与算法] 强化学习：动态规划，蒙特卡罗

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 强化学习：动态规划，蒙特卡罗 -> 正文阅读

[数据结构与算法]强化学习：动态规划，蒙特卡罗

1，动态规划

1.1，基本原理

动态规划是求解决策过最优化的数学方法，其基本思想是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。适合于用动态规划求解的问题，经分解得到的子问题往往不是互相对立的，因次解决子问题的时候，其结果通常需要存储起来以解决后续复杂问题。这样就可以避免大量的重复计算，节省时间。

当问题具有以下特征时，可以考虑使用动态规划来求解：

一个复杂的最优解由数个小问题的最优解构成，可以通过寻找子问题的最优解来得到复杂问题的最优解。
子问题在复杂问题内重复出现，使得子问题的解可以被存储起来重复利用。

马尔可夫决策过程（MDP）具有上述两个特性。贝尔曼方程把问题问题递归为求解子问题，价值函数相当于存储了一些子问题的解，可以复用。因此可以使用动态规划来求解马尔可夫决策过程（MDP）。

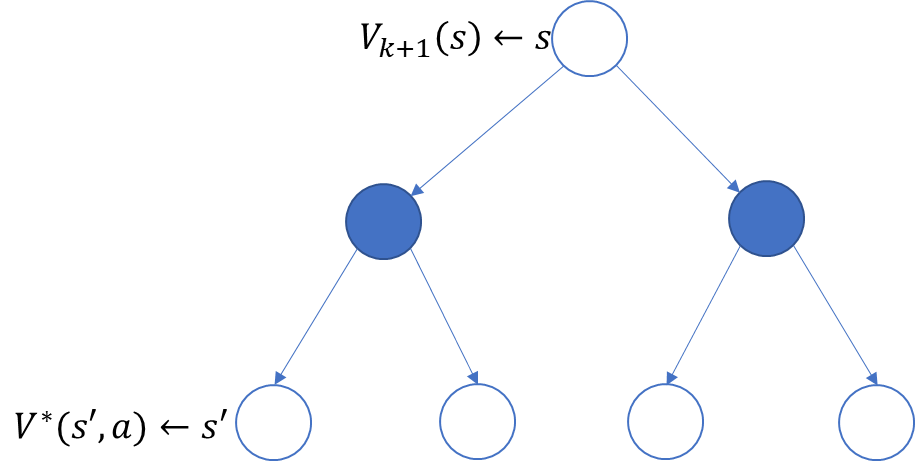
使用动态规划算法求解马尔可夫决策过程（MDP）模型，也就是在清楚模型结构（包括状态转移率、回报率等）的基础上，用动态规划方法来进行策略评估和策略改进，最终获得最优策略。

策略评估（预测）：给定一个马尔可夫决策过程模型MDP： $<S,A,P,R,\gamma>$ ?和一个策略? $\pi$ ?，要求输出基于当前策略? $\pi$ ?的所有状态的值函数? $V$ 。
策略改进（控制）：给定一个马尔可夫决策过程模型MDP： $<S,A,P,R,\gamma>$ ?和一个策略? $\pi$ ?，要求确定最优值函数? $V^{*}$ ?和最优策略? $\pi^{*}$ 。

1.2，策略评估

策略评估要解决的问题是，给定一个策略? $\pi$ ，如何计算在该策略下的值函数? $V_{\pi}$ 。因为实际中涉及的马尔可夫模型规模一般比较大，直接求解效率低，因此可使用迭代法进行求解。考虑应用贝尔曼期望方程进行迭代：

$V_{\pi}(s)=\sum_{a\in A}\pi(a|s)\left ( R_s^a + \gamma \sum_{s^{'}\in S}P_{ss^{'}}^aV_{\pi}(s^{'}) \right )$

状态? $s$ ?处的值函数? $V_{\pi}(s)$ ，可以利用后继状态? $s^{'}$ ?的值函数? $V_{\pi}(s^{'})$ ?来表示，依次类推。

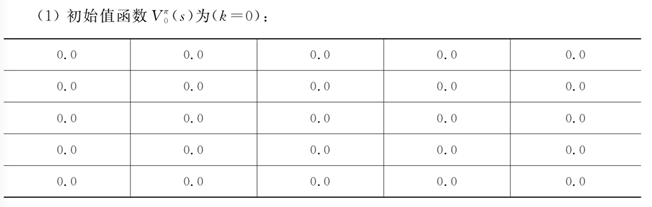
初始所有状态值函数（ $V$ ）全部为：0 ，第 k+1 次迭代求解? $V_{\pi}(s)$ ?时，使用第? $k$ ?次计算出来的值函数? $V_k(s^{'})$ ?更新计算? $V_{k+1}(s)$ ?。迭代时使用公式如下：

$V_{k+1}(s)=\sum_{a\in A}\pi(a|s)\left ( R_s^a + \gamma \sum_{s^{'}\in S}P_{ss^{'}}^aV_{k}(s^{'}) \right )$

对于模型已知的强化学习算法，概率和回报都是已知数，唯一的未知数是值函数，因此该方法通过反复迭代最终将收敛。

1.3，策略改进

计算值函数的目的是利用值函数找到最优策略。既然值函数已经获得，接下来要解决的问题是如何利用值函数进行策略改善，从而得到最优策略。

一个很自然的方法是针对每个状态采用贪心策略对当前策略进行改进，即：

$\pi_{l+1}(s)\in arg \underset{a}{max}Q_{\pi_{l}}(s,a)$

其中， $Q_{\pi}(s,a)=R_s^a+\gamma\sum_{s^{'}\in S}P_{ss^{'}}^aV_{\pi}(s^{'})$

在当前策略? $\pi$ ?的基础上，利用贪心算法选取行为，直接将所选择的动作改变为当前最优的动作。

令动作改变后对应的策略? $\pi^{'}$ ， $a^{'}$ ?为在状态? $s$ ?下遵循策略? $\pi^{'}$ ?选取的动作，同理? $a^{''}$ ?为在状态? $s^{'}$ ?下遵循策略? $\pi^{'}$ ?选取的动作。改变动作的条件是? $Q_{\pi}(s,a^{'})\geqslant V_{\pi}(s)$ ，则可得到：?

$\large V_{\pi}(s)\leqslant Q_{\pi}(s,a^{'})=R_s^{a^{'}}+\sum_{s^{'}\in S}\gamma P_{ss^{'}}^a^{'}V_{\pi}(s^{'})\leqslant R_s^{a^{'}}+\sum_{s^{'}\in S}\gamma P_{ss^{'}}^a^{'}Q_{\pi}(s^{'},a^{''})=...=V_{\pi^{'}}(s)$

可见，值函数对于策略的每一点改进都是单调递增的，因此对于当前策略? $\pi$ ，可以放心地将其改进。

$\large \pi^{'}= arg \, \, \underset{a \in A}{max}\, \, Q_{\pi}(s,a)$

直到? $\large \pi^{'}$ ?与? $\large \pi$ ?一致，不再变化，收敛至最优策略。

贪心这个词在计算机领域是指在对问题求解时，总是做出在当前看来是最好的选择，不从整体最优上加以考虑，仅对短期行为（即一步搜索）求得局部最优解。将贪心算法应用在强化学习中求解最优策略函数实际上可以获得全局最优解，因为贪心策略公式中的值函数? $\large V_{\pi}(s),Q_{\pi}(s,a)$ ?已经考虑了未来的回报。因此在策略改进时，可以放心使用贪心算法求得全局最优解。

1.4，策略迭代

将策略评估算法和策略改进算法合起来便有了策略迭代算法。策略迭代算法通常由策略评估和策略改进两部分构成：

在策略评估中，根据当前策略计算值函数。
在策略改进中，通过贪心算法选择最大值函数对应的行为。

策略评估和策略改进两部分交替进行不断迭代。

假设我们有一个初始策略? $\large \pi_1$ ，策略迭代算法首先评估该策略的价值（用 $\large E$ ?表示），得到该策略的价值函数? $\large V_{\pi_1}$ ?或? $\large Q_{\pi_1}$ ?，下一步，策略迭代算法会借助贪心算法对初始策略? $\large \pi_1$ ?进行改进（用 $\large I$ ?表示），得到? $\large \pi_2$ 。接着对改进后的策略? $\large \pi_2$ ?进行评估，在进一步改进当前策略，如此循环迭代，直到策略收敛至最优。

? $\large \pi_1\overset{E}{\rightarrow }V_{\pi_1},Q_{\pi_1} \overset{I}{\rightarrow }\pi_2 \overset{E}{\rightarrow }V_{\pi_2},Q_{\pi_2} \overset{I}{\rightarrow }...\pi^* \overset{E}{\rightarrow }V^*,Q^* \overset{I}{\rightarrow } \pi^*$

其中， $\large \pi_1$ ?为初始策略， $\large E$ ?表示策略评估， $\large I$ ?表示策略改进。策略评估过程中，对于任意的策略? $\large \pi_k$ ，通过贝尔曼方程进行迭代计算得到? $\large V_{\pi_k},Q_{\pi_k}$ ?。

$\large V_{\pi_k}(s)=V_k^{\pi_k}(s)=\sum_{a\in A}\pi_k(a|s)\left ( R_s^a+\gamma\sum_{s^{'}\in S}P_{ss^{'}}^aV_{k-1}^{\pi_k}(s^{'}) \right )$

策略改进部分，用贪心算法得到更新策略：

$\large \pi^{'}(s)=arg\, \, \underset{a\in A}{max}Q_{\pi_k}(s,a)$

或

$\large \pi^{'}(s)=arg \, \, \underset{a\in A}{max}\left [ R_s^a +\gamma \sum_{s^{'}\in S}P_{ss^{'}}^aV_{\pi_k}(s^{'})\right ]$

在策略评估过程中，往往需要等到值函数收敛之后才能进行策略改进，这其实是没有必要的。可以在进行一次策略评估之后就开始策略改进，如此循环往复执行这两个过程，最终会收敛到最优值函数和最优策略。

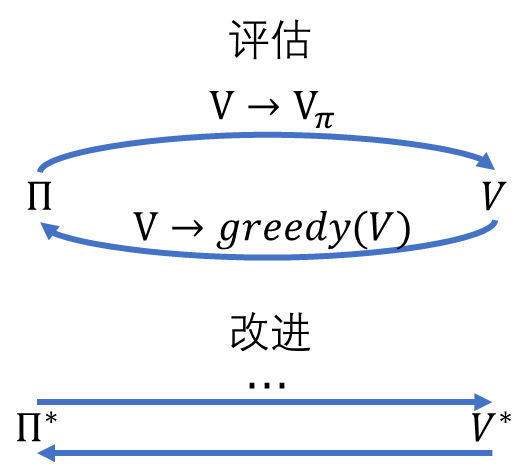
广义策略迭代（generalized policy iteration：GPI）：

GPI包含两个过程：策略评估和策略改进，两者可以以各种粒度交错进行。（如：值函数收敛之后进行策略改进，也可以进行一次策略评估之后就开始策略改进）
几乎所有强化学习方法都可以被描述为GPI，是一个普遍的方法。
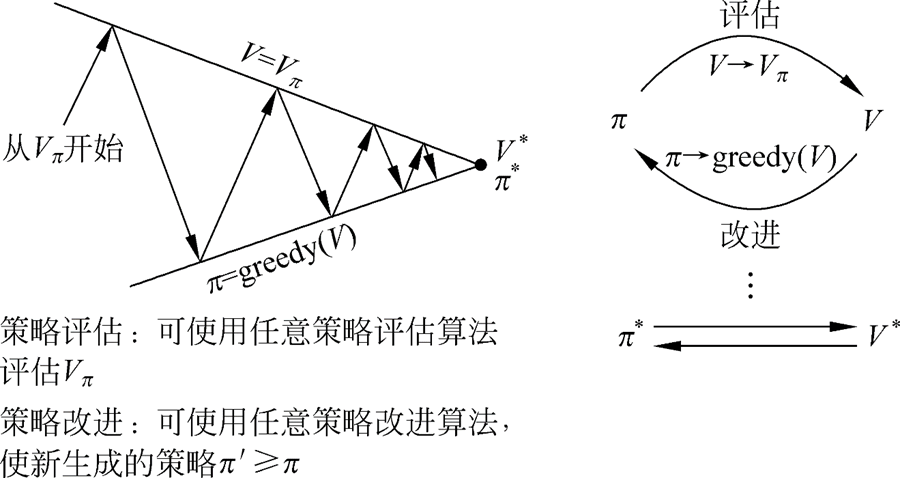
评估、改进过程稳定，不再发生变化，则得到最优值函数和最优策略。
评估、改进过程可看作竞争与合作的过程，都把对方往相反地方拉，最终得到最优解。
直接朝着一个目标会导致远离另一个目标。联合过程更接近优化总目标。

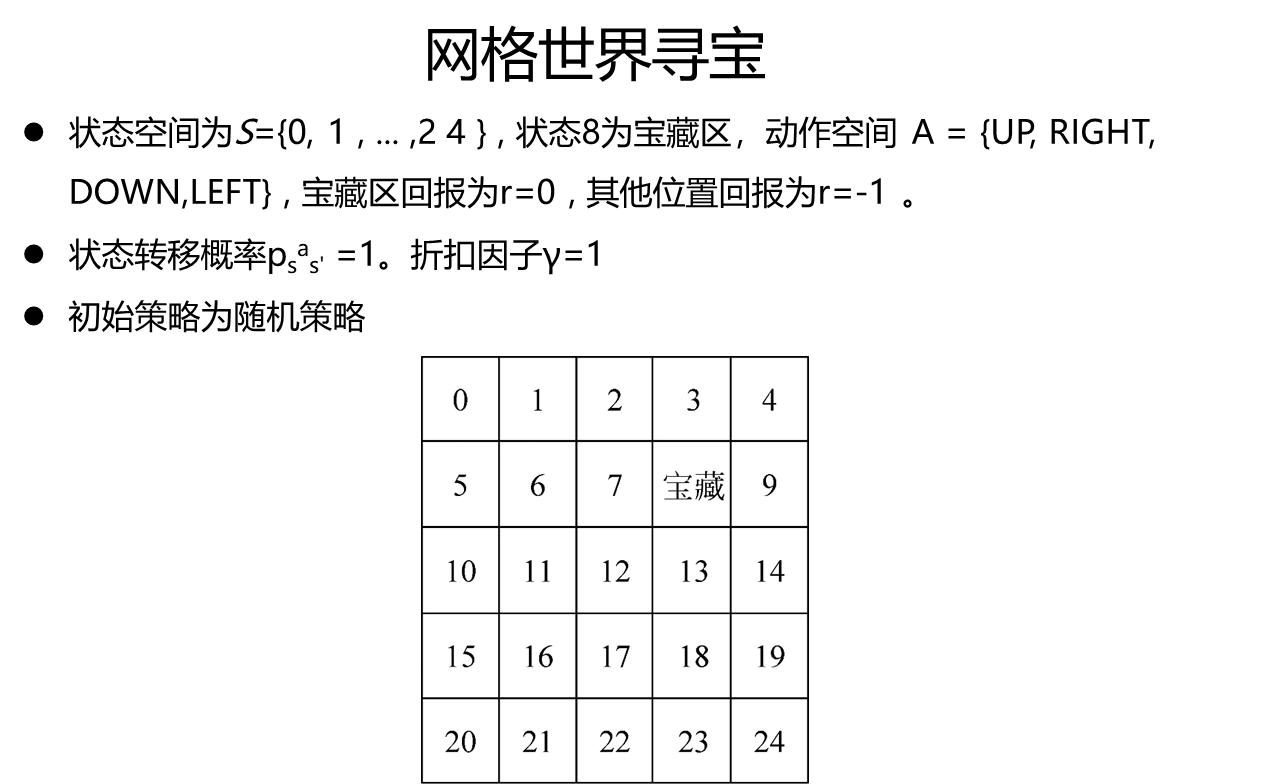
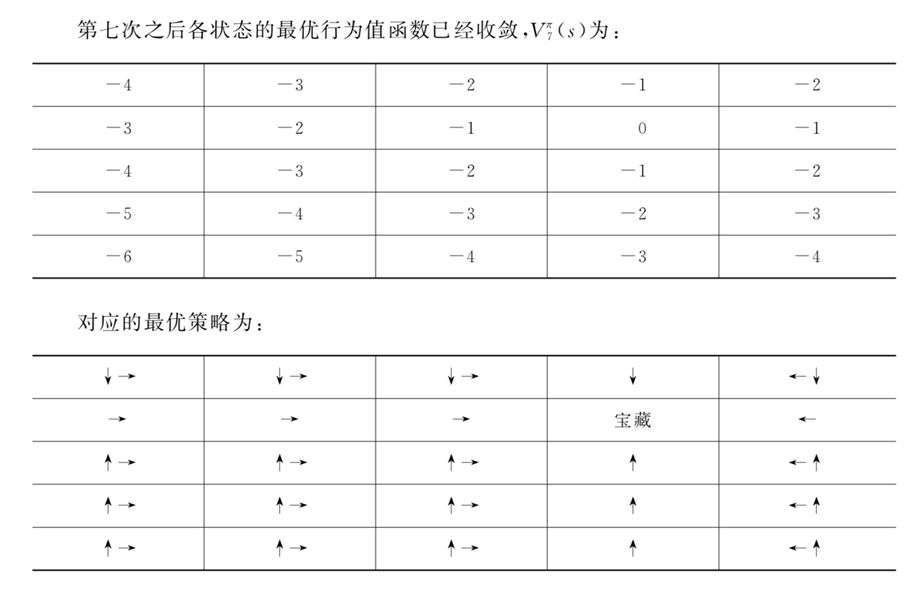
1.5，策略迭代（案例）

当智能体位于网格世界边缘时，任何使其离开网格世界的行为都会使其停留在当前位置。

使用策略迭代法对此问题求解，假设初始策略为均匀随机策略：

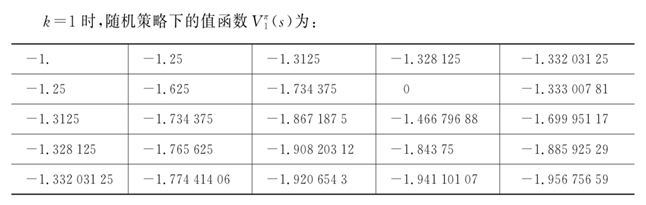
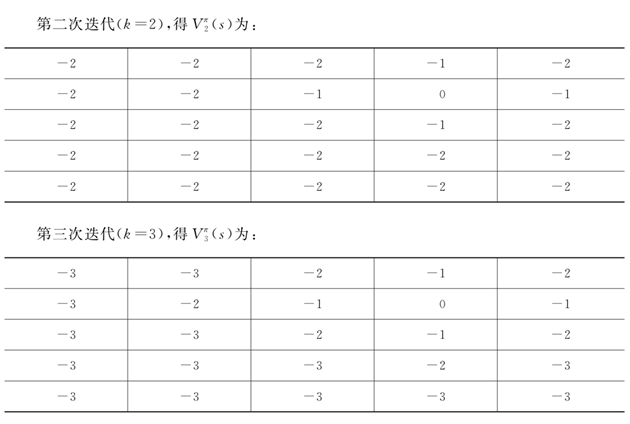
$\small \pi(UP|\cdot )=0.25;\pi(RIGHT|\cdot )=0.25;\pi(DOWN|\cdot )=0.25;\pi(LEFT|\cdot )=0.25$

（1）首先评估给定随机策略下的值函数，使用贝尔曼期望方程迭代计算直至值函数收敛。初始化所有状态值函数为0，使用如下公式进行迭代值函数：

$\small V_{k+1}(s)=\sum_{a\in A}\pi(a|s)\left ( R_s^a + \gamma \sum_{s^{'}\in S}P_{ss^{'}}^aV_{k}(s^{'}) \right )$

其中， $\small R_s^a$ ?表示当前状态的期望，而不是目标状态的期望。

$\small V_k(s^{'})$ ?表示目标状态的状态值。

? $\small V_1(s=0)=0.5(-1+1*1*0)+0.25(-1+1*1*0)+0.25(-1+1*1*0)=-1$

$\small V_1(s=1)=0.25(-1+1*1*0)+0.5(-1+1*1*0)+0.25(-1+1*1*-1)=-1.25$

$\small V_1(s=2)=0.75(-1+1*1*0)+0.25(-1+1*1*(-1.25))=-1.3125$

$\tiny V_1(s=3)=0.5(-1+1*1*0)+0.25(-1+1*1*(-1.3125))+0.25(-1+1*1*0)=1.328125$

......

（2）使用如下公式：

$\large \pi^{*}(a|s)=arg \, \, \underset{a\in A}{max}\left [ R_s^a +\gamma \sum_{s^{'}\in S}P_{ss^{'}}^aV^*(s^{'})\right ]$

对收敛的值函数? $V_{338}^{\pi}(s)$ ，使用贪心算法进行策略改进，求取? $V_{338}^{\pi}(s)$ ?对应的改进后策略? $\pi_1$ ，则有 $\pi_1$ ：

$\pi(a=UP\, or\, LEFT|s=0)=-1+1*1*(-47.13614306)=-48.13614306$

$\pi(a=RIGHT|s=0)=-1+1*1*(-41.72708685)=-42.13614306$

$\pi(a=DOWN|s=0)=-1+1*1*(-48.54523094)=-49.54523094$

$\pi^{*}(s=0)=\pi^{*}(a=RIGHT|s=0)=-42.13614306$

......

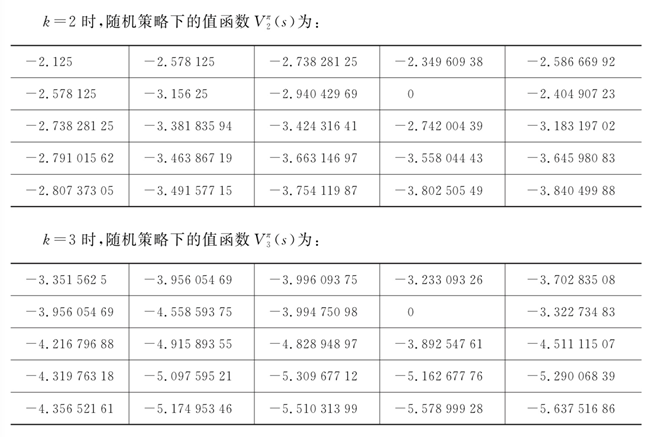
继续使用贝尔曼期望方程求取当前策略? $\pi_1$ ?下的值函数，直至值函数收敛，过程同（1）：

针对值函数? $V_5^{\pi_1}(s)$ ?进行第二次策略改善，得到? $\pi_2$

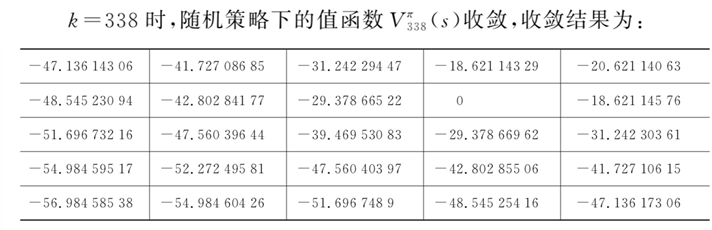
继续求取? $\pi_2$ ?对应的值函数（策略评估），针对收敛的值函数?? $V_5^{\pi_2}(s)$ ?进行改进，得到? $\pi_3$

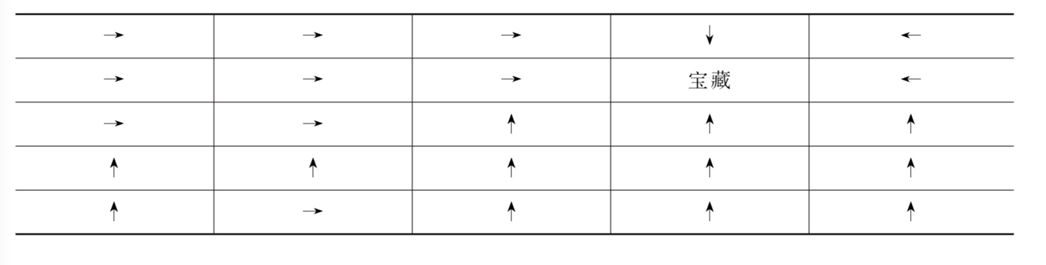
经过三次策略改进，策略收敛。

1.6，值迭代

策略迭代算法在每次进行策略评估时，采用贝尔曼期望方程更新值函数。而值迭代算法借助的是贝尔曼最优方程，直接使用行为回报的最大值更新原来的值。

$V_{k+1}(s)=\underset{a\in A}{max}\left ( R_s^a +\gamma \sum_{s^{'}\in S}P_{ss^{'}}^aV_k(s^{'}) \right )$

值迭代算法将策略改进视为值函数的改善，每一步都求取最大的值函数，即：

$V_1\rightarrow V_2\rightarrow V_3\rightarrow ...\rightarrow V^*$

假设在状态? $s$ ?下，有一个初始值函数? $V_1(s)$ ，基于当前状态，有多个可选行为? $a$ 。每个行为? $a$ 会引发一个立即回报? $R_s^a$ ?，一个或多个状态转移，如从状态? $s$ ?转换至状态 $s^{'}$ ?。不同状态? $s^{'}$ ?对应有不同的值函数? $V_1(s^{'})$ ?整个的? $R_s^a+\gamma \sum_{s^{'}\in S}P_{ss^{'}}^aV_1(s)$ ?称为? $a$ ?的回报。值迭代直接使用所有行为引发的行为回报中取值最大的那个值来更新原来的值，得到? $V_2(s)$ ?。如此迭代下去，直至值函数收敛，整个过程没有遵循任何策略。

虽然算法中没有给出明确的策略，但是根据公式：

$V_{t+1}(s)\leftarrow \underset{a\in A}{max}Q_{t+1}(s,a)$

可以看出策略迭代改进是隐含在值迭代过程中执行的。

1.7，值迭代（案例）

在进行一次策略评估（即求出当前策略下的值函数）之后就进行策略改进，这种方法被称为值函数迭代算法。即，在每次进行值函数计算时，直接选择那个是的值函数最大的行为。

2，蒙特卡罗

2.1，基本原理

动态规划是基于模型的强化学习方法，但在实际情况下，环境的状态转移概率及回报往往很难得知，此种情况下，动态规划就不再使用了。这时候可考虑采用无模型方法通过采样的方式替代策略评估，蒙特卡罗方法就是基于这个思想。

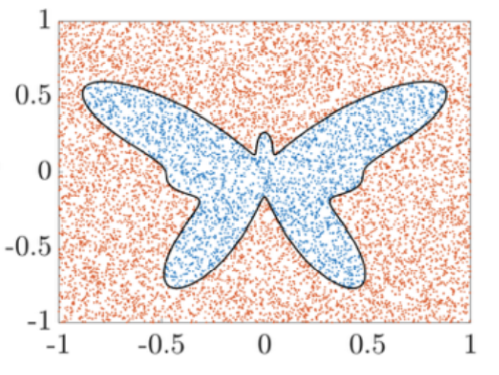
蒙特卡罗方法也称为统计模拟方法（或称统计实验法），是一种基于概率与统计的数值计算方法。该计算方法的主要核心是通过对建立的数学模型进行大量随机试验，利用概率论求得原始问题的近似解，与它对应的是确定性算法。

例如：计算图中蝴蝶的面积，可以通过随机撒豆子，统计在蝴蝶中豆子的比例进而计算蝴蝶的面积。

蒙特卡罗算法的核心思想是，在问题领域进行随机抽样，通过不断、反复、大量的抽样后，统计结果，得到解空间上关于问题领域的接近真实的分布。

蒙特卡罗强化学习在进行策略评估时，通过多次采样产生轨迹，求取平均累计回报作为期望累计回报的近似。整个蒙特卡罗强化学习使用了广义策略迭代框架，由策略评估和策略改进两部分组成，一次策略评估后面紧跟着对当前策略的改进，两个步骤交互进行，直至获得最优策略。

2.2，蒙特卡罗评估

蒙特卡罗评估是通过学习智能体与环境交互的完整轨迹来估计值函数的。所谓完整轨迹是指，从一个起始状态开始，使用某种策略一步步执行动作，直至结束形成的经验信息，包括所有时间步的状态、行为、立即回报等。

假设共执行? $T$ ?步，形成的完整轨迹如下： $<s_0,a_0,r_0,s_1,a_1,r_1,...,s_T,a_T,r_T>$

使用蒙特卡罗方法评估策略时，对评估方法做了三点改变：

因为是无模型的方法，无法通过贝尔曼方程迭代获得值函数，因此通过统计多个轨迹中累计回报的平均数对值函数进行估计。
在求累计回报平均时采用增量更新的方式进行更新，避免了批量更新方法中对历史数据的存储，提高来计算效率。
为了方便直接从估计对象中求解最优策略，蒙特卡罗将估计值函数? $V$ ?改为估计行为值函数? $Q$ ，这样可通过贪心策略直接获得最优行为。

利用平均累计回报估计值函数

值函数、行为值函数：

$V_{\pi}(s)=E_{\pi}\left [ G_t|S_t=s \right ]=E_{\pi}\left [ R_{t+1}+\gamma R_{t+2}+...|S_t=s \right ]$

$Q_{\pi}(s,a)=E_{\pi}\left [ R_{t+1}+\gamma R_{t+2}+...|S_t=s \right ]=E_{\pi}\left [ \sum_{k=0}^{\infty } \gamma ^kR_{t+k+1}|S_t=s\right ]$

可见，状态值函数、行为值函数的计算实际上是计算累计回报的期望。在没有模型时，可以采用蒙特卡罗方法进行采样，产生经验信息。这些经验性信息经验性地推导出每个状态? $s$ ?的平均回报，以此来替代回报的期望，而后者就是状态值函数。状态值函数的估计通常需要掌握完整的估计才能准确计算得到。

当要评估智能体的当前策略? $\pi$ ?时，可以利用策略? $\pi$ 产生多个轨迹，每个轨迹都是从任意的初始状态开始直到终止状态，例如下面多个完整的轨迹：

轨迹1： $<s_0,a_0,r_{11},s_1,a_1,r_{12},...,s_1,a_2,r_{1k},...,s_{T},a_{T},r_{1T}>$
轨迹2： $<s_0,a_0,r_{21},s_3,a_1,r_{22},...,s_1,a_k,r_{2k},...,s_{T},a_{T},r_{2T}>$
......

计算一个轨迹中状态处? $s$ ?的基类回报返回值为：

$G_t=r_{t+1}+\gamma r_{t+2}+...=\sum_{k=0}^{\infty }\gamma ^{k}r_{t+k+1}$

为计算方便，轨迹中用累计回报代替立即回报，则上面的轨迹表达式可表示为：

轨迹1： $<s_0,a_0,G_{11},s_1,a_1,G_{12},...,s_1,a_2,G_{1k},...,s_{T},a_{T},G_{1T}>$
轨迹2： $<s_0,a_0,G_{21},s_3,a_1,G_{22},...,s_1,a_k,G_{2k},...,s_{T},a_{T},G_{2T}>$
......

在状态转移过程中，可能发生一个状态经过一定的转移后又一次或多次返回该状态，此时在多个轨迹里如何计算整个状态的平均回报呢？有两种方法：第一次访问蒙特卡罗方法（初访）和每次访问蒙特卡罗方法（每访）。

初访是指，在计算状态? $s$ ?处的值函数时，只利用每个轨迹中第一次访问到状态? $s$ ?时的累计回报。如轨迹1中，状态? $s_1$ ?出现了两次，但计算状态? $s_1$ ?处累计回报均值时只利用? $s_1$ ?初次出现的累计回报? $G_{12}$ （不计算 $s_1$ ?第二次出现后的累计回报 $G_{1k}$ ）。轨迹2中，状态? $s_1$ ?仅出现了一次，其累计回报为? $G_{2k}$ 。因此初访法计算? $V(s_1)$ ?的公式为：

$V(s_1)=\frac{G_{12}+G_{2k}+...}{N(s_1)}$

其中， $N(s_1)$ ?表示包含状态? $s_1$ ?的轨迹数。

每访法是指，在计算状态? $s$ ?处的值函数时，利用所有访问到状态? $s$ ?时的累计回报。如轨迹1，计算状态? $s_1$ ?处的均值时需要用到? $G_{12},G_{1k}$ ?。因此，每访法计算? $V(s_1)$ ?的公式为：

$V(s_1)=\frac{G_{12}+G_{1k}+G_{2k}+...}{N(s_1)}$

其中， $N(s_1)$ ?表示状态? $s_1$ ?出现的总次数。

蒙特卡罗方法是用统计的方法求取值函数的，根据大数定律：当样本数量足够多的时候，即? $N(s_1)$ ?无穷大时，根据样本求取的值函数? $V(s_1)$ ?接近于真实值函数 $V_{\pi}(s_1)$ ?。

增量式更新

通常，蒙特卡罗法再求平均值到时候采用批处理进行的，即在一个完整的采样轨迹完成后，对全部的累计回报进行更新。实际上，这个更新过程可以增量式进行，使得在计算平均值时不需要存储所有既往累计回报，而是每得到一个累计回报之后就计算其平均值。

对于状态? $s_t$ ，不妨设基于? $k$ （初访法? $k$ ?指的是含有状态 $s_t$ ?的轨迹书，每访法指的是状态 $s_t$ 的数目）个采样数据估计出值函数为? $V(s_1)$ ，增量公式：

$V_k=\frac{1}{k}\sum_{j=1}^kG_j=\frac{1}{k}\left ( G_k+\sum_{j=1}^{k-1}G_j \right )$

$=\frac{1}{k}\left ( G_k+(k-1)V_{k-1} \right )$

$=V_{k-1}+\frac{1}{k}\left ( G_k-V_{k-1} \right )$

则在得到第? $k+1$ ?个采样数据? $G_t(s_t)$ ?状态对应累计回报时，有：

$V_{k+1}\leftarrow V_k(s_t)+\frac{1}{k+1}\left ( G_{k+1}(s_t)-V_k(s_t) \right )$

可简写为：

$V(s_t)\leftarrow V(s_t)+\frac{1}{k+1}\left ( G_t -V(s_t)\right )$

显然，只需要给? $V(s_t)$ ?加上? $\frac{1}{k+1}\left ( G_t-V(s_t) \right )$ ?即可，更一般地，将? $\frac{1}{k+1}$ ?替换为常数? $\alpha$ ?, 令? $1>\alpha >0$ ?，表示更新步长， $\alpha$ ?越大，代表越靠后的累回报报越重要。

最终得到蒙特卡罗方法值函数估计的更新公式：

$V(s_t)\leftarrow V(s_t)+\alpha (G_t-V(s_t))$

估计行为值函数? $Q$ ?代替估计值函数? $V$

动态规划中的策略迭代算法估计的是值函数? $V$ ，而最终的策略通过行为值函数? $Q$ ?获得，或者下一个状态的? $V$ ?获得。当模型已知的时候，从值函数? $V$ ?到行为函数? $Q$ ?有一个很简单的转换公式，可以根据此公式求解? $\pi^{'}(s)$ ：

$\pi^{'}(s)=arg\,\underset{a\in A} {max}\,Q(s,a)$

同时因为知道? $P_{ss^{'}}^a$ ?和? $R_s^a$ ，也可以根据如下公式求解

$\pi^{'}(s)=arg\, \underset{a\in A}{max}\, \left [ R_s^a+\gamma \sum_{s^{'}\in S}P_{ss^{'}}^aV(s^{'}) \right ]$