基于多目标粒子群算法在分布式电源选址和定容中的应用matlab程序
摘 要: 为更好地解决分布式电源选址定容问题,提出一种改进的多目标粒子群算法。考虑投资成本、网损以及电压稳定性三因素建立了一个三目标的数学模型,并采用上述多目标粒子群算法对模型求解。最后利用 IEEE-69节点系统仿真来验证所提算法在分布式电源选址定容方面的有效性。
关键词: 分布式电源; 选址定容; 多目标粒子群
1 含有分布式电源的配电网结构
分布式电源接入配电网前后的情况如图 1、图 2所示。
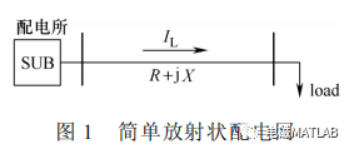
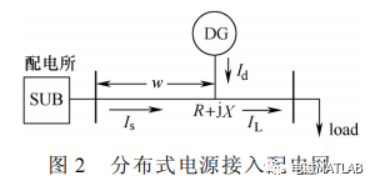
图中,R+jX 表示线路总阻抗;w 表示 DG 接入配电网后距离配电所端的距离占线路总长度的 w%;IL、 IS 和 Id 分别代表负荷端电流、配电所端注入电流、分布式电源注入电流;设 PL、QL 分别代表负荷端有功功率和无功功率;U 表示负荷端电压;PG、QG分别代表 DG 端有功功率和无功功率;LossLA、LossLB 分别表示图 1 和图 2 中的网络损耗?。
当不考虑 DG 时,有
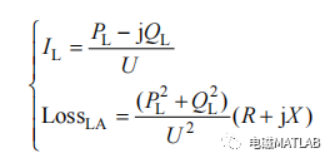
考虑到 DG 的注入功率时,配电网网络损耗可划分为两部分:①SUB-DG 之间线路损耗;②DG-load 之间线路损耗。可推导出
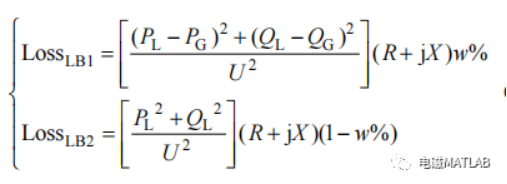
因此整个网络损耗为
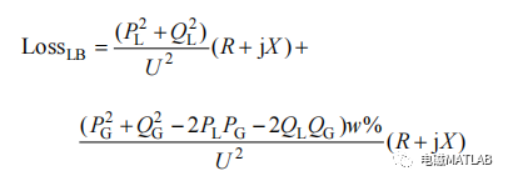
分布式电源接入前后的网络损耗变化可以由以上推导出
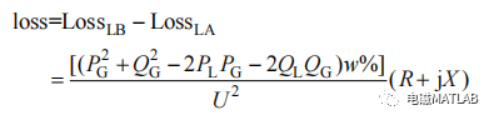
可见,分布式电源接入后与接入前对网络损耗的影响主要取决于配电所端和分布式电源端功率的大小。
2 含 DG 的配电网优化配置模型2.1 目标函数
( 1) 投资与运行成本
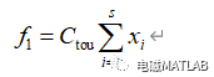
( 2) 配电网总有功网损
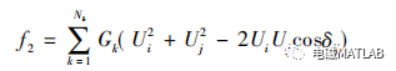
( 3) 配电网电压安全稳定性
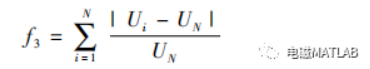
式中: r 是折现率; k 是设备使用年限; s 为 DG 接入系统的节点数; xi 为接入 DG 的有功容量; Nb 为系统中的支路数; N 为网络节点数; UN 为额定电压,取 1. 05; Ui 表示实际电压幅值。
2.2 约束条件
(1) 等式约束条件
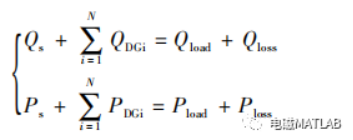
(2) 不等式约束条件
?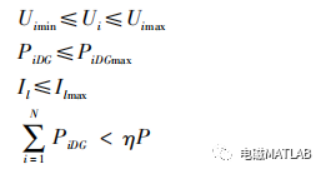
3 算例
IEEE69节点系统结构
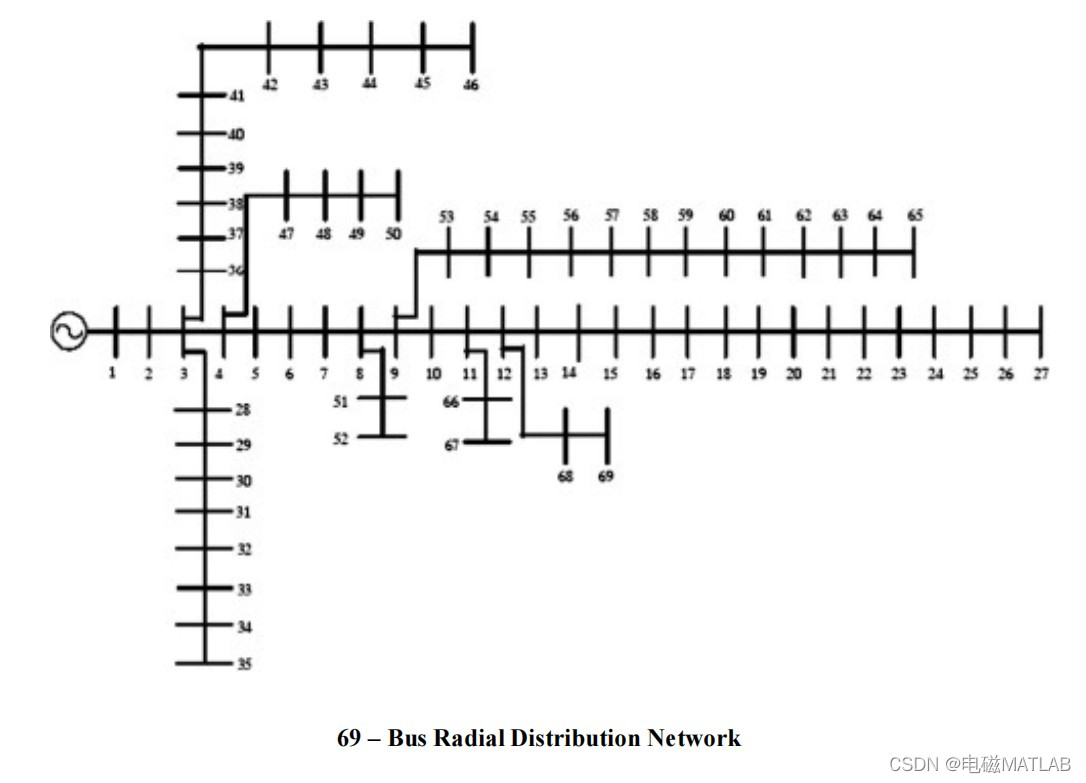
IEEE69节点系统参数
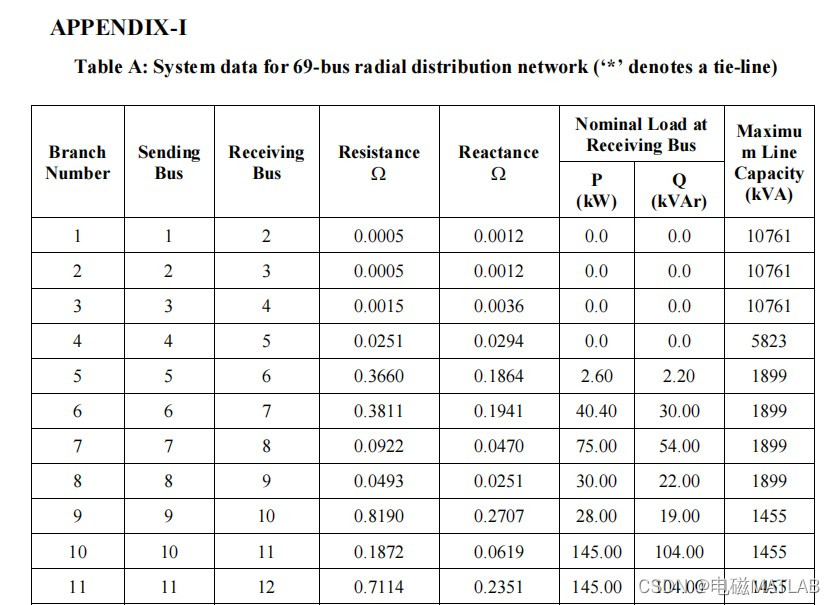
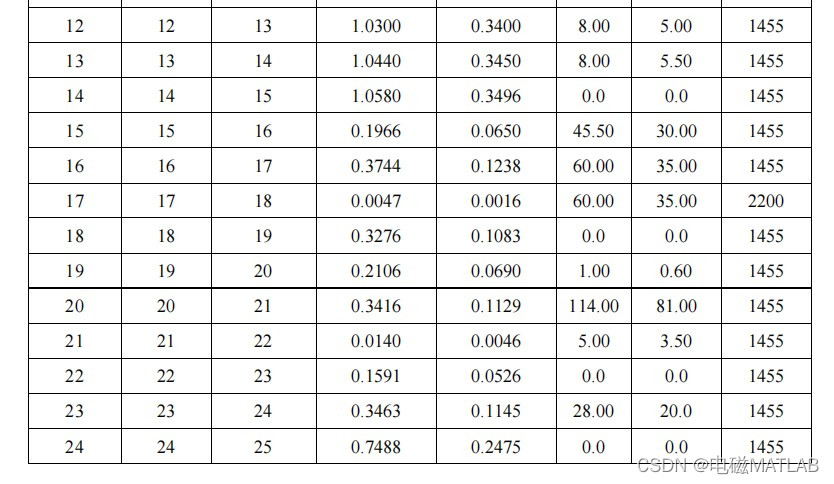
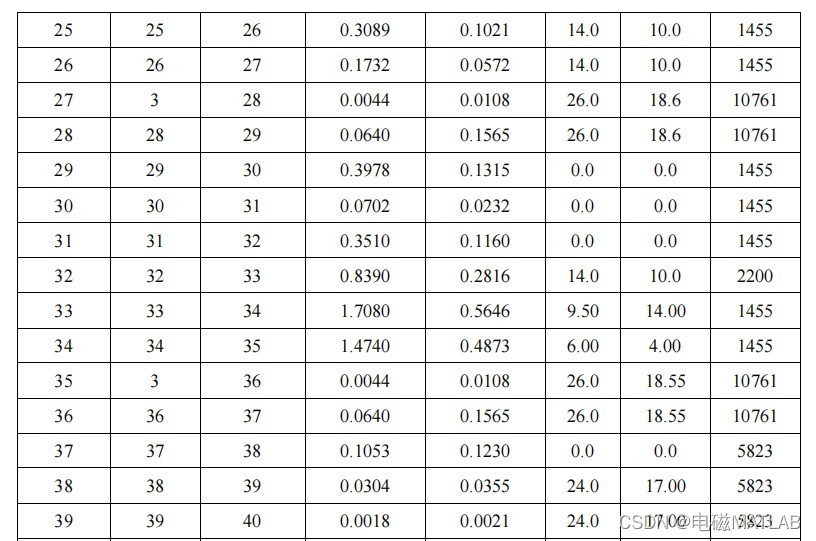
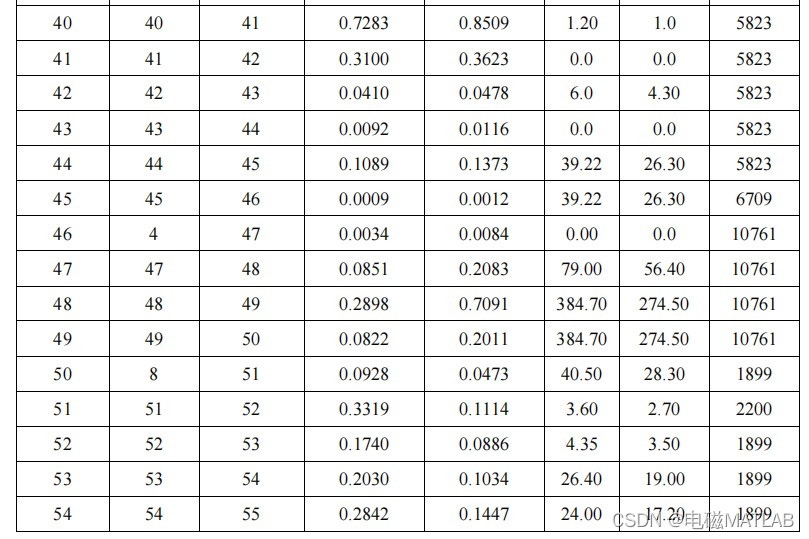
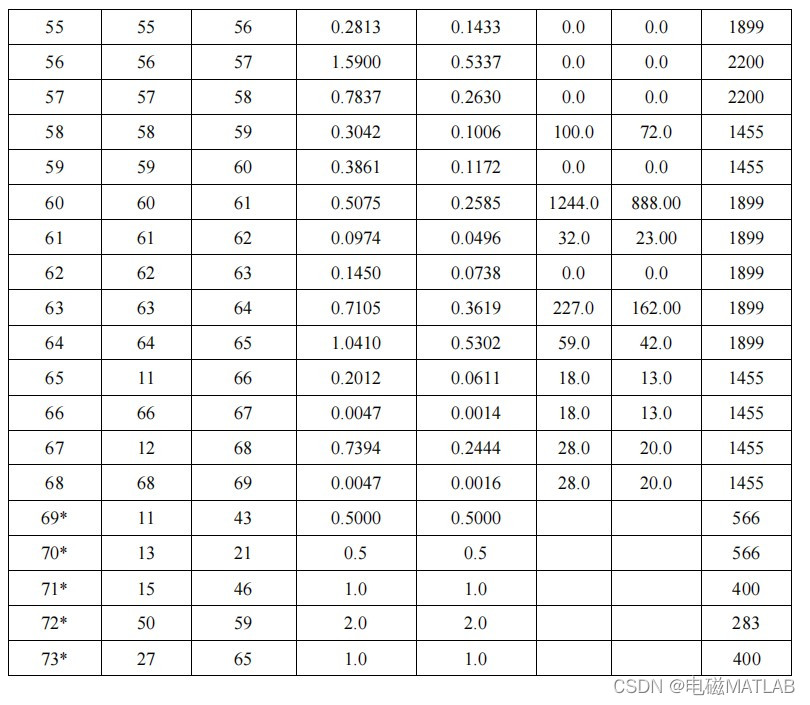
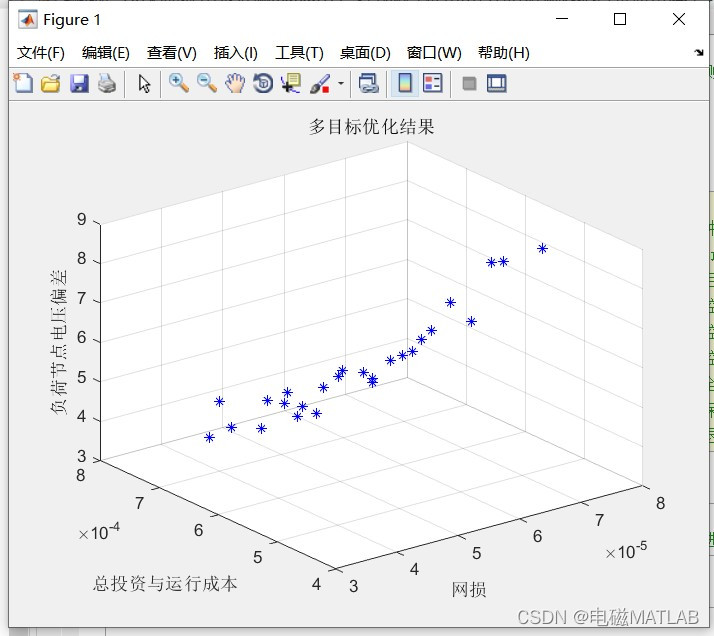
4 程序运行结果
5 matlab程序
%% 多目标粒子群算法分布式电源定容选址优化规划
tic %测试时间
format short ;
clc;
clear
close all
%% 算法初始参数设置
pop=90; %种群粒子数目
gen=200; %最大迭代次数
M=4; %目标函数个数(M-1)
V=68; %控制变量个数
Xmax=10; %控制变量约束最大值
Xmin=0; %控制变量约束最小值
g_best=zeros(gen,V); %全局最优存放位置
pop_num=50; %保存的最优前沿
lamda=0.5; %退火常数
%% 初始化种群个体
[pop_x,pop_v]=initial(pop,V,M);
%% 模拟退火粒子群算法
for t=1:gen %进入主要循环,gen迭代次数
clear Gbest_value
clear R
%% 1.寻找全局最优
[pbest,pbest_value,k]=gbest_fitness(pop_x,V,M,pop);
g_best(t,:)=pbest;
g_best_value(t,:)=pbest_value;
%% 1.对各目标函数值进行排序
for j = 1 : M
[Gbest_value(:,j),R(:,j)]=sort(g_best_value(:,j));
end
%% 2.根据个体排序计算其适应度
for i = 1 : t
for j = 1 : M
if R(i,j)>1
ex(i,j)=(pop-R(i,j))^2;
else
ex(i,j)=k*pop;
end
end
end
ex=sum(ex');
%% 3.得到适应度最好的全局最优解
[Fit,index]=sort(ex');
%[y_val,index]=min(g_best_value);
clear Fit;
gbest=g_best(index,:);
%% 2.速度更新
change_v=update_v(t,gen,pop_v,pop_x(:,1:68),g_best,V,pop,pbest);
pop_v=change_v;
%% 2.更新位置
change_x=pop_x(:,1:V)+change_v(:,1:V);
%% 控制变量约束
for i = 1 : pop
for j = 1 : V
if change_x(i,j)>Xmax
change_x(i,j)=randi([0,10],1,1);
else if change_x(i,j)<Xmin
change_x(i,j)=randi([0,10],1,1);
end
end
end
end
%% 粒子群速度限制约束
%% 求出各个体的目标函数值
for i=1:pop
change_x(i,V+1:V+M)=mokuaihanshu(pop_x(i,:),pop,M,V);%求出各个体的目标函数值
end
%% 形成混合种群
[y1,x1]=size(pop_x);
[y2,x2]=size(change_x);%注意:此时x1不等于x2
migle_x(1:y1,:)=pop_x;
migle_x(y1+1:y1+y2,1:x2)=change_x;
%% 进行非支配排序
migle_x = non_domination_sort_mod(migle_x, M, V);
%% 选择下一代种群
pop_x = replace_chromosome(migle_x, M, V, pop);
%% 画图输出
Ploss=pop_x(:,V+1)./(10^9);
Cost=pop_x(:,V+2)./(10^6);
plot3(Ploss,Cost,pop_x(:,V + 3),'b*');
xlabel('网损');ylabel('总投资与运行成本');zlabel('负荷节点电压偏差');
grid on
hold off
title('多目标优化结果')
drawnow
end
pop_x(1:(V+3))
。。。。。。。。略
详细程序转链接:https://mp.weixin.qq.com/s?__biz=Mzg4MTc1MjE2Mg==&mid=2247483847&idx=1&sn=ab3ab8d21cbd5a4018e0b4bb4ce4d8d3&chksm=cf6060caf817e9dc1daffe28e9f818915dfe6da30b6a4d3cad6d92100cbf6b6b37e3ed43617b&token=1687758221&lang=zh_CN#rd
感谢阅读,欢迎关注“电磁matlab”