题目描述
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环。
所有边的长度都是 1,点的编号为 1~n。
请你求出 1 号点到 n 号点的最短距离,如果从 1 号点无法走到 n 号点,输出 ?1。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 a 和 b,表示存在一条从 a 走到 b 的长度为 1 的边。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
数据范围
1
≤
n
,
m
≤
1
0
5
1≤n,m≤10^5
1≤n,m≤105
输入样例:
4 5
1 2
2 3
3 4
1 3
1 4
输出样例:
1
思路
本题提到了最短距离,我们很容易想到广度优先遍历,就是通过对图进行广度优先遍历,从而划分层次,然后即可得到1-n的最短距离。
这里再次使用了广度优先遍历的模板和图的存储方式的模板:
图的存储方式模板:
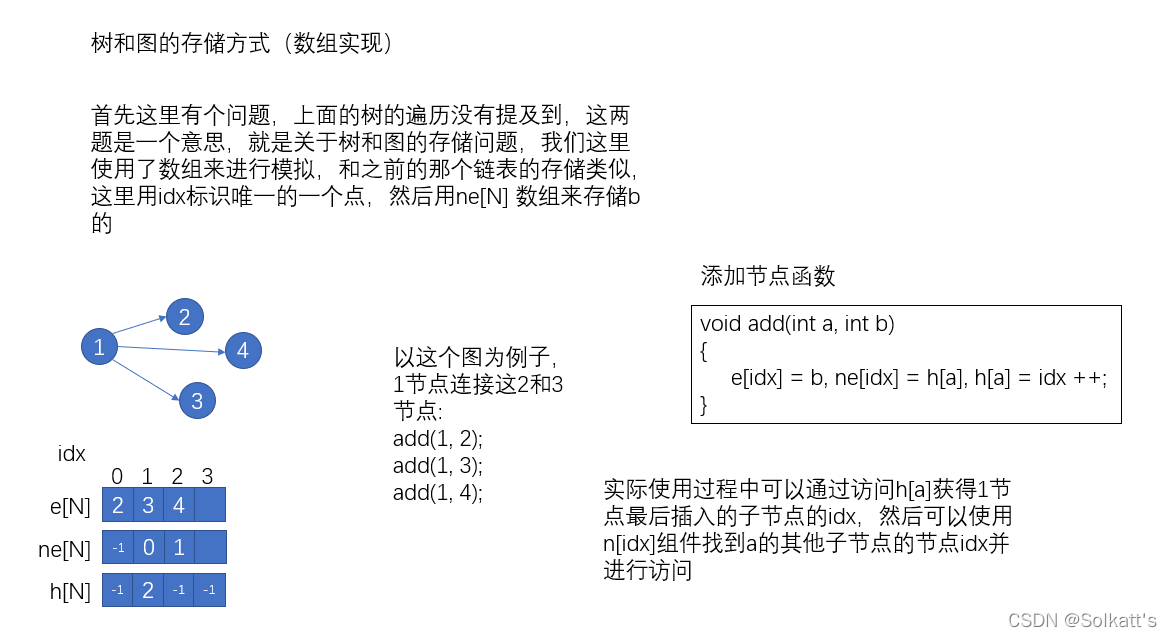
void add(int a, int b)
{
// 这里表示通过h 可以定位到a的下一个连接节点 因为a可能有多个连接节点
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
广度优先遍历模板:

int bfs()
{
int hh = 0, tt = 0;
q[0] = 1;
memset(d, -1, sizeof d);//将d初始值设置为-1
d[1] = 0;// 设置起始点的距离为0
while(hh <= tt)
{
int t= q[hh ++];
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(d[j] == -1)
{
d[j] = d[t] + 1; // 距离+ 1
q[++ tt] = j;//插入队尾
}
}
}
return d[n];
}
代码示例
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;// 有向图存储
int n, m;
int d[N], q[N]; // 距离和队列
void add(int a, int b)
{
// 这里表示通过h 可以定位到a的下一个连接节点 因为a可能有多个连接节点
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int bfs()
{
int hh = 0, tt = 0;
q[0] = 1;
memset(d, -1, sizeof d);//将d初始值设置为-1
d[1] = 0;// 设置起始点的距离为0
while(hh <= tt)
{
int t= q[hh ++];
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(d[j] == -1)
{
d[j] = d[t] + 1; // 距离+ 1
q[++ tt] = j;//插入队尾
}
}
}
return d[n];
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 0; i < m; i ++)
{
int a, b;
cin >> a >> b;
add(a, b);
}
cout << bfs() << endl;
return 0;
}