机器学习—吴恩达_ 第9周_学习总结
21.11.1-21.11.6
👉周学习任务:
- 90% SVM
一、SVM(支持向量机)
支持向量机是在二分类的问题中找到一个最有把握把两类样本分开的一个超平面(最优超平面), 既然是最优问题,就需要先把找最优超平面的问题用数学的方式表示出来,得到了原始的优化目标(SVM原始问题),但是该原始问题对于参数会有约束,不太好求出最优超平面,于是转成无约束问题,并借助凸优化的相关理论把其转成等价的对偶问题,最后通过求对偶问题的解得到最终的超平面。




SVM优缺点:
-
优点:
- 严格的数学理论支持, 可解释强。
- 能找出对任务至关重要的样本(支持向量)。
- 由于SVM是一个凸优化问题,所以求得的解一定是全局最优而不是局部最优。
- 不仅适用于线性线性问题还适用于非线性问题(用核技巧)。
- 拥有高维样本空间的数据也能用SVM,这是因为 SVM 对偶形式求解的复杂度与样本数量而不是维数相关,因此 SVM 很擅长解决高维稀疏的问题。
-
缺点:
- 二次规划问题求解将涉及m mm阶矩阵的计算(m mm为样本的个数), 因此SVM不适用于超大数据集。(SMO算法可以缓解这个问题)。
- 模型预测时,预测时间与支持向量的个数成正比。当支持向量的数量较大时,预测计算复杂度较高。因此支持向量机目前只适合小批量样本的任务,无法适应百万甚至上亿样本的任务。
- 当样本数量比较大时,效果通常不如神经网络。
吴大恩:
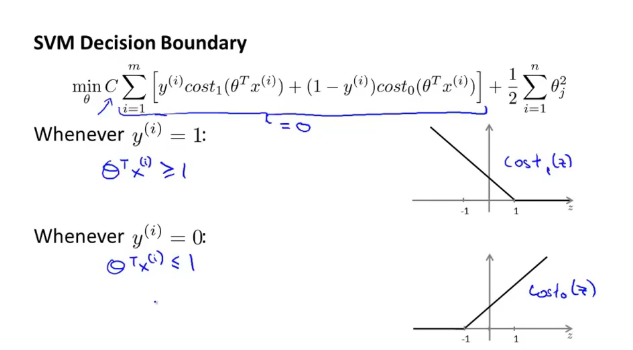
当训练集Y=1的时候,要想上面的值为0,则cost1=0的时候,z>=1
当训练集Y=0的时候,要想上面的值为0,则cost0=0的时候,z<=-1
- 1和-1就是一个安全距离,决策边界

当C很大的时候:使得内部值为0
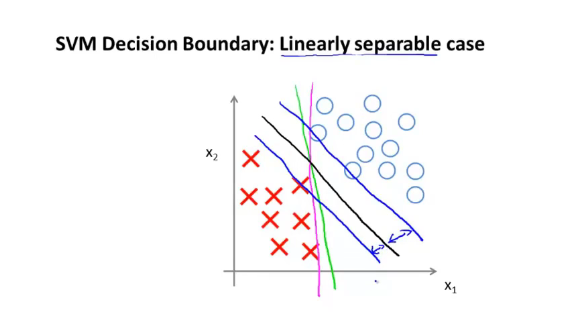
下面的案例是多个直线划分正负样本,存在蓝色线的margin,叫SVm的间距,具有鲁棒性(越大越好),最大分类器
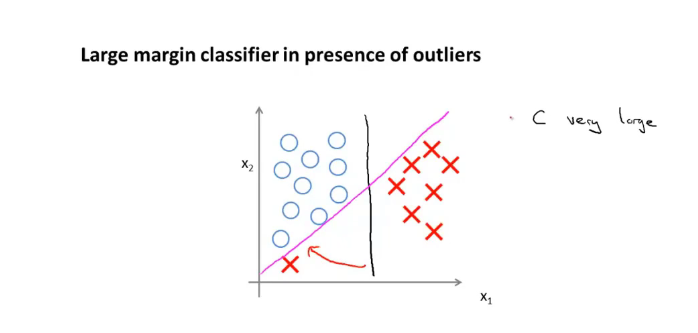
当c非常大的时候,会将黑线变成紫线,但是紫线的情况非常不好,C的作用类似于KaTeX parse error: Undefined control sequence: \y at position 2: 1\?y? ,C不是很大的时候,可能会得到黑线
大间隔分类器的理解
回顾向量内积:根据毕达哥拉斯定理会得到向量积
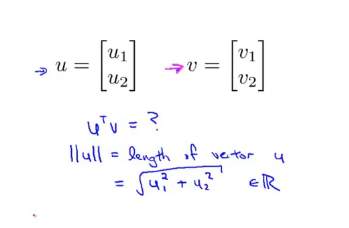
两个向量的乘积: V*U的乘积,实际上是P在V在U上的投影乘以u的范数。V*U=P*||u||
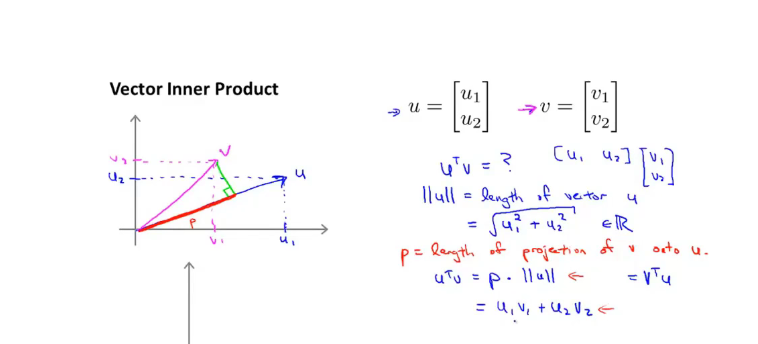
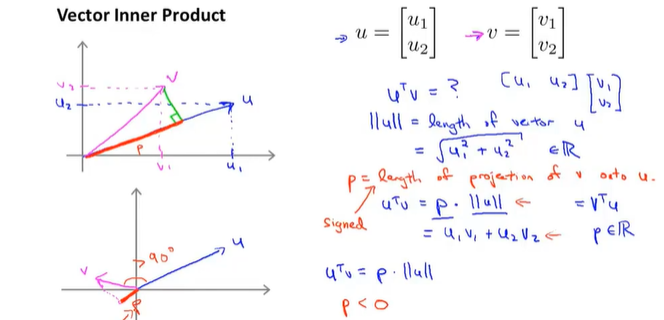
u是一个向量,可以理解为参数的向量(x为 θ 1 \theta_1 θ1?,y轴为 θ 2 \theta_2 θ2?),V向量位置可以理解为样本的位置,样本对u向量做投影,会存在为正为负的情况,就是正样本和负样本,其划分线是u的垂线。
向量的范数:

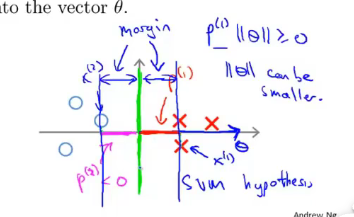
θ 0 \theta_0 θ0?为0的时候,从原点出发,x的位置在 θ \theta θ的投影就是 p i p^i pi 然后其 θ T X i = p i ∣ ∣ θ ∣ ∣ \theta^TX^i=p^i ||\theta|| θTXi=pi∣∣θ∣∣ 值大于1 正样本。类似于 ∣ x ∣ ? ∣ θ ∣ ? c o s 夹 角 |x|*|\theta|*cos夹角 ∣x∣?∣θ∣?cos夹角。
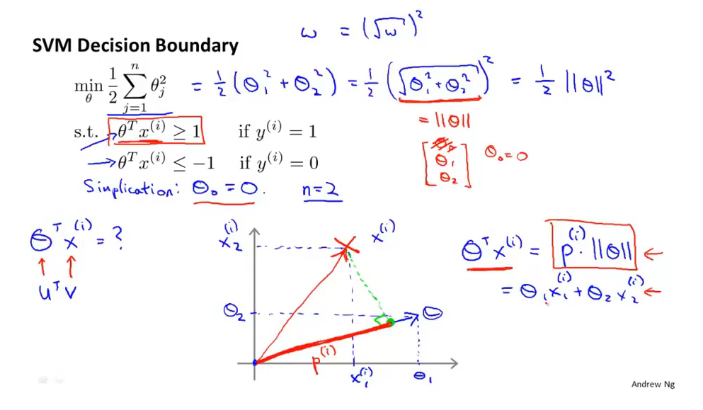
上图具体是指训练样本x在theta上的投影。
向量参数实际上是和 θ \theta θ成正交的。

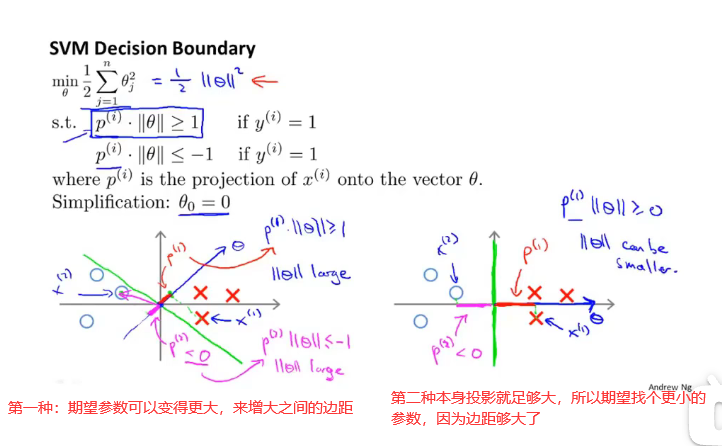
svm原理:
- 支持向量机的目标函数就是努力寻找最大边界,也称为大间距分类器,这个最大边界即是样本在 θ \theta θ上的投影。要增大边界,就是想办法增大他们的投影,最后取出较小的 θ \theta θ值。
核函数
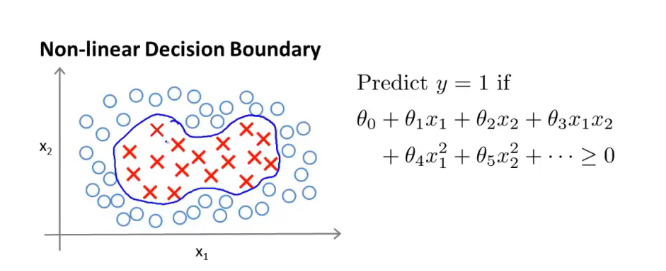
- 构造复杂的多项式可以画出这个图像,但是很多高阶函数我们并不知道是否适用,同时高阶太多会导致计算量增大,而核函数是一个更加有效的解决办法

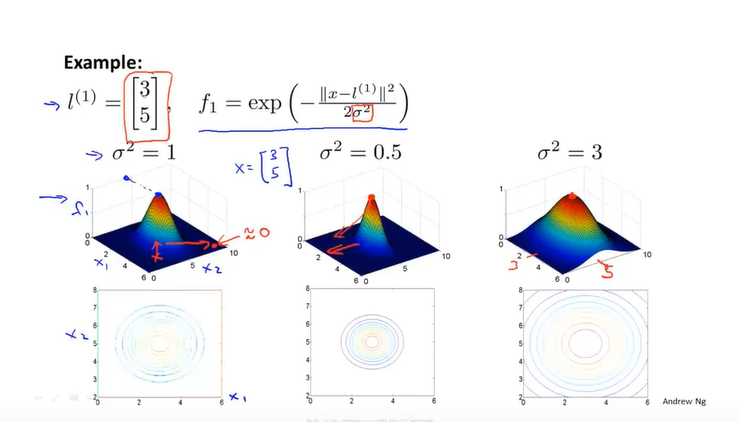
这里案例是高斯核函数,相似函数,x与标记点之间的位置越近越为1,反之

当标记的值为3.5时,当分母为1时,f的高度约为1。
- 标记点的选择:将所有的样本点设置为标记点
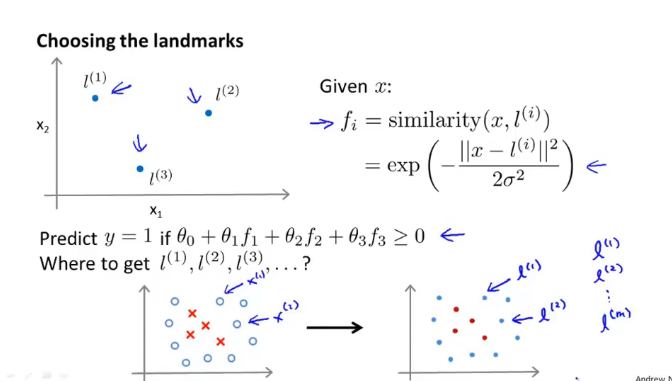

- 算出所有的x与其他标记点之间的位置距离,也可以是相似度

