任务一：

首先导入数据

直接使用import Data 那个按键，选中Excel表

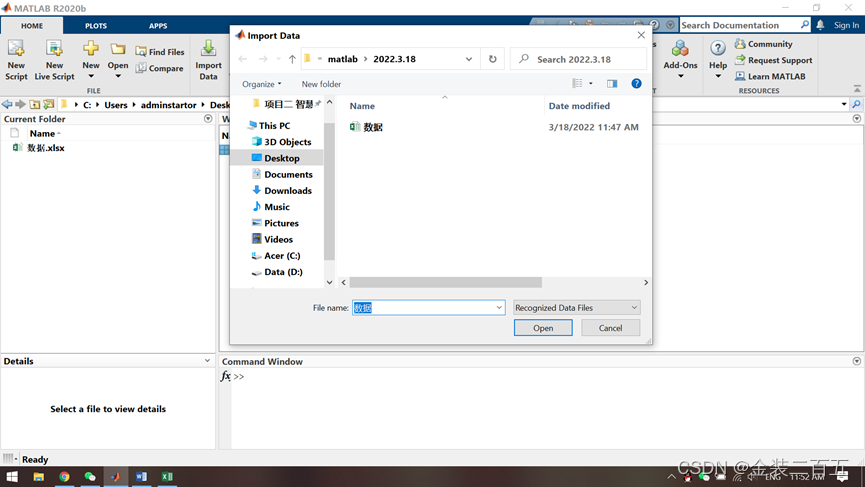
在这里插入图片描述

将数据输出类型选择为矩阵

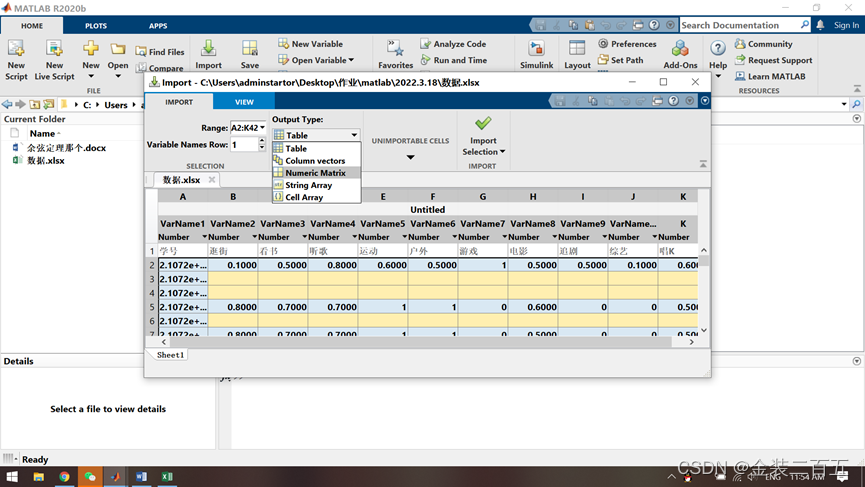
在这里插入图片描述

而且import的选项选择为导入数据

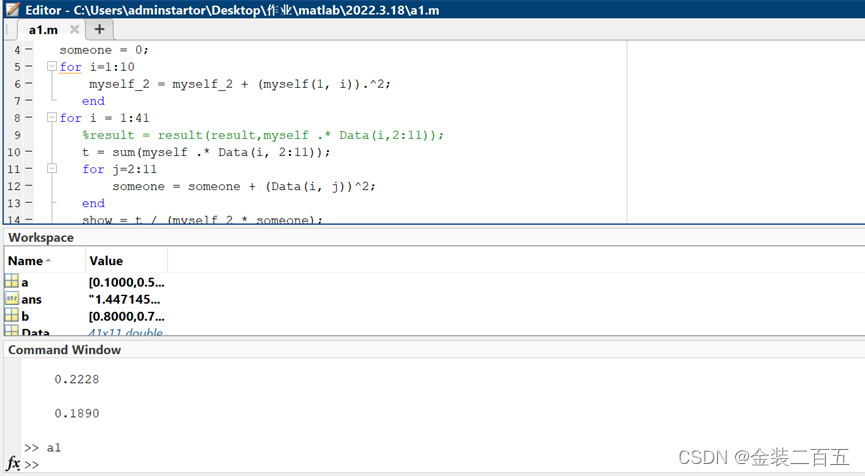
在这里插入图片描述

计算自己与班上志同道合的同学：

myself = Data(29, 2:11);
myself_2 = 0;
someone = 0;
for i = 1:10  % 先计算出自己的向量的模
    myself_2 = myself_2 + (myself(1, i)).^2;   
   end
for i = 1:41 %计算向量的值
      t = sum(myself .* Data(i, 2:11));
   for j = 2:11 %计算其他人向量的模，虽然会重复计算一次自己的值，但是，不用太在意
       someone = someone + (Data(i, j))^2;
   end
   show = t / (sqrt(myself_2) * sqrt(someone)); %使用余弦定理进行计算
   if (show > 0.9)
       disp(Data(i, 1));
   end
   someone = 0;
end

这里的乘法都需要点乘，因为是向量的数量积
如果是在计算向量的模的时候，使用到某位上面的一个数的时候，这个时候用不用点乘都无所谓了，因为这就是普通的两个数之间进行的乘法
每次进行计算前，需要使用循环将向量的模计算出来

结果如下：

在这里插入图片描述

计算分组：

水平有限，仅供参考

person = [];
mo = [];
mo_result = 0;
result = zeros(41,41); %用于最后分组的计算
for i = 1:41
    for j = 2:11   
       mo_result = mo_result + (Data(i,j))^2;
    end
    mo(end + 1) = sqrt(mo_result);
    mo_result = 0;
end
mo_2 = mo'; %先进行向量转置，使计算的时候行向量碰上一个列向量，因为一个向量里面装的是全部人的模，使他转置是为了可以让每个人都一一对应，最终的结果可以形成一个41 * 41的矩阵

%上面这部分先进行向量的模的计算，将41个向量的模全部算出来，存放在一个一行，41列的向量中，方便后面计算


for i = 1:41
    for j = 1:41 %进行余弦值计算
        t = (sum(Data(i, 2:11) .* Data(j, 2:11))) ./ (mo(i) .* mo_2(j));
        result(i, j) = t;
        if (t > 0.9)
            result(i, j) = 1;
        else
            result(i, j) = 0;
        end
    end
end
%将计算出来的结果简化， 如果两个之间的余弦值大于0.9 ， 则表示为1 ，否则就表示为0

ans = 0; %存放当前这个组里面的人数有多少
ans_2 = 0; %存放当前的组数
group = []; %存放每个组里面的成员编号，根据成员编号可以找到对应的学号

%进一步优化可以考虑使用一个哈希表，让学号和成员编号一一对应，因为班里面的学号并不是一个严格的公差为一的等差数列
 
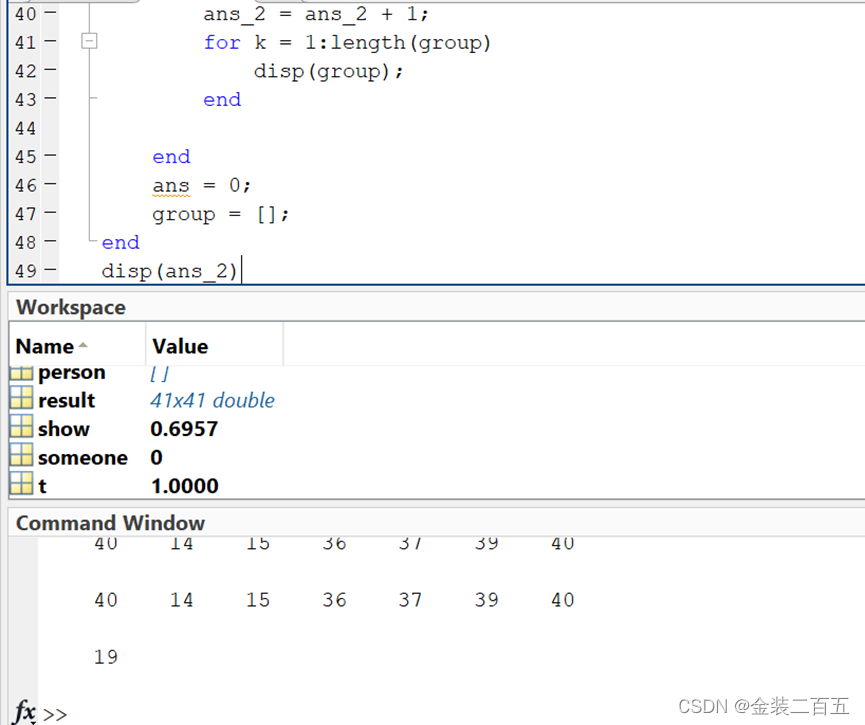
for i = 1:41
    group(end + 1) = i;
    for j = 1:41
         if result(i, j) == 1 && result(j, i) == 1 % 判断是否凑成一组
             ans = ans + 1; % 组员数加一
             group(end + 1) = j; 将当前的组员编号添加进去
         end
    end
    if ans >= 4 % 如果组员数量大于4才输出，否则不输出
        ans_2 = ans_2 + 1; 
        for k = 1:length(group)
            disp(group); 
        end
        
    end
    ans = 0; % 清零，方便进入下一次计算
    group = []; % 清零 方便进入下一次计算
end
disp(ans_2) %显示最终结果