[数据结构与算法]求答案3（找规律+取余）

题目描述

现有一个序列a1,a2,a3,···,an。
求

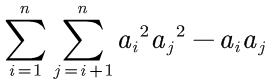
由于答案可能较大，所以输出结果取模1e9+7
输入
输入包含多组样例。第一行一个整数T(0<=T<=104)–代表测试样例的组数。
接下来T组数据
每组数据第一行包含一个整数n(1<=n<=105)–代表数组的长度。
接下来是一个实数序列a1,a2,a3,···,an(0<ai<=109)–数组元素。
保证n在所有用例中不超过105。

输出
每组样例输出一个整数代表答案
样例输入
4
2
1 2
3
1 2 3
4
1 2 3 4
5
1 2 3 4 5
样例输出
2
38
238
938

题意

对于长为 n 的数组 a ，求

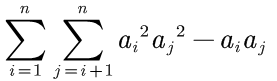
思路

n 取较小值时，写出求和式子，从中找规律。
例 n == 5时，

ans的另一种形式：

如图所示，我们只需要记录前面各个数 和 及 平方的和 即可一个for循环求出答案。
我刚开始一直没过，没有考虑到负数取余的情况（见注释）。
提示：和、积、差的余数 分别视为 和、积、差的余数。

代码

#include <iostream>
#include <cstdio>
#include <queue>
#include <set>
#include <algorithm>

using namespace std;
typedef unsigned long long ll;
const ll N = 1e5+10, M = 1e9+7;

ll a[N];
int main()
{
    int t;
    scanf("%d",&t);
    while(t--){
        int n;ll tem;
        scanf("%d",&n);
        ll s1=0, s2=0, ans = 0;
        for(int i=0;i<n;i++){
            scanf("%llu",&a[i]);
            if(i>0){
                ans += ((a[i]*a[i])%M * s1)%M;
                ans = ans%M;
                ans = (ans - (a[i]*s2)%M + M)%M;//+ M 防止负数对 M 取余
            }

            s1+=(a[i]*a[i])%M;
            s1%=M;
            s2+=a[i];
            s2%=M;
        }
        printf("%llu\n",ans);
    }
    return 0;
}