[数据结构与算法]DFS、BFS系列

前言

BFS、DFS即广度、深度优先搜索，常见于图的遍历，不过在树中的递归遍历和层次遍历，也是这两个思想。

一、案例

二、题解

package com.xhu.offer.offerII;

import java.util.ArrayDeque;
import java.util.Queue;

//岛屿的最大面积
public class MaxAreaOfIsland {
    //DFS-component + mark数组-plugin(该plugin可以用grid被遍历过的值赋值为0即可)
    public int maxAreaOfIsland(int[][] grid) {
        int m = grid.length, n = grid[0].length;

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] != 0) {
                    dfs(grid, i, j);
                    max = max < count ? count : max;
                }
            }
        }
        return max;
    }

    int count = 0;
    int max = 0;

    private void dfs(int[][] grid, int i, int j) {
        if (i == -1 || j == -1 || i == grid.length || j == grid[0].length || grid[i][j] == 0) return;

        count++;
        grid[i][j] = 0;
        dfs(grid, i + 1, j);
        dfs(grid, i - 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i, j - 1);
    }

    //BFS-component + mark数组-plugin(该plugin可以用grid被遍历过的值赋值为0即可)
    public int maxAreaOfIsland2(int[][] grid) {
        int m = grid.length, n = grid[0].length;

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] != 0) {
                    Queue<int[]> t = new ArrayDeque<>();
                    t.offer(new int[]{i, j});
                    grid[i][j] = 0;
                    int count = bfs(grid, t);
                    max = max < count ? count : max;
                }
            }
        }
        return max;
    }

    private int bfs(int[][] grid, Queue<int[]> queue) {
        int count = 1;
        while (!queue.isEmpty()) {
            int[] t = queue.poll();
            grid[t[0]][t[1]] = 0;

            if (t[0] - 1 != -1 && grid[t[0] - 1][t[1]] != 0) {
                queue.offer(new int[]{t[0] - 1, t[1]});
                grid[t[0] - 1][t[1]] = 0;
                count++;
            }
            if (t[0] + 1 != grid.length && grid[t[0] + 1][t[1]] != 0) {
                queue.offer(new int[]{t[0] + 1, t[1]});
                grid[t[0] + 1][t[1]] = 0;
                count++;
            }
            if (t[1] - 1 != -1 && grid[t[0]][t[1] - 1] != 0) {
                queue.offer(new int[]{t[0], t[1] - 1});
                grid[t[0]][t[1] - 1] = 0;
                count++;
            }
            if (t[1] + 1 != grid[0].length && grid[t[0]][t[1] + 1] != 0) {
                queue.offer(new int[]{t[0], t[1] + 1});
                grid[t[0]][t[1] + 1] = 0;
                count++;
            }
        }
        return count;
    }
}

总结

1）掌握好DFS、BFS的前提是掌握好递归思想即拆解相同小问题思想，以及队列的使用。

参考文献

[1] LeetCode 岛屿的最大面积

附录

1、二分图

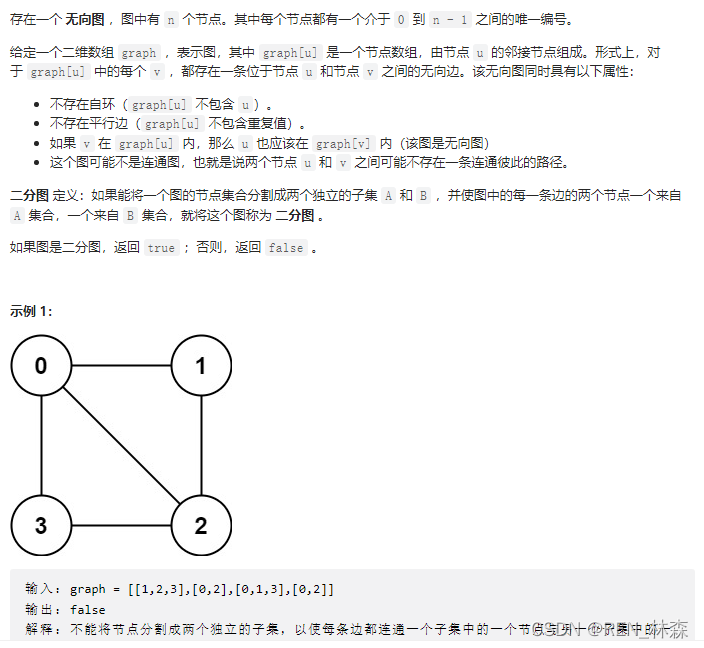
package com.xhu.offer.offerII;

import java.util.HashMap;
import java.util.Map;

//二分图
public class IsBipartite {
    //DFS-component + HashMap记录状态-plugin
    //核心思路：通过DFS将连通分量里的节点分别分到0，1两种状态，用map存储，若能不能成功分开，返回false，否则返回true。不成功即节点的多个state & 1不相等。
    public boolean isBipartite(int[][] graph) {
        Map<Integer, Integer> m = new HashMap<>();

        int len = graph.length;
        for (int i = 0; i < len; i++) {
            if (graph[i].length == 0) continue;

            if (!m.containsKey(i) && !dfs(graph, i, m, 0)) return false;
        }
        return true;
    }

    private boolean dfs(int[][] graph, int i, Map<Integer, Integer> m, int state) {
        m.put(i, state & 1);

        int len = graph[i].length;
        for (int j = 0; j < len; j++) {
            if (m.containsKey(graph[i][j])) {
                if (m.get(graph[i][j]) == (state & 1)) return false;
                continue;
            }
            if (!dfs(graph, graph[i][j], m, state + 1)) return false;
        }
        return true;
    }

    //调试
    //bug1:dfs(graph,graph[i][j],m,state + 1)，不是dfs(graph,j,m,state+1)，毕竟数组长度不一。
    public static void main(String[] args) {
        new IsBipartite().isBipartite(new int[][]{{1}, {0, 3}, {3}, {1, 2}});
    }
}