[数据结构与算法]【数据结构】堆排序的算法复杂度分析

说明：阅读本文章的前提是对堆排序过程有大致了解，此处重点讲解算法的复杂度

堆排序的过程

每次交换堆顶元素和堆底元素之后，待排序元素个数就少一个

初始状态

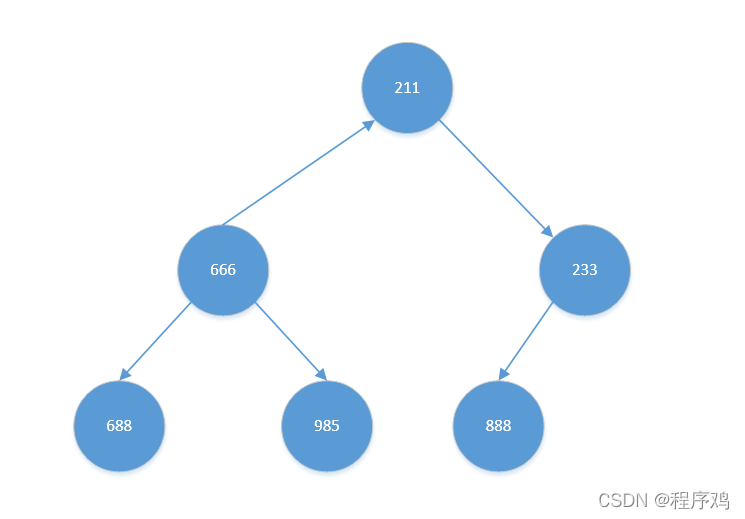
建立初始堆（大根堆）

依次从后往前逐渐调整，只考虑非叶子节点（分支节点），第一个调整的元素为“最后一个非叶子节点”，即【233】

1. 考虑【233】

其左孩子为【888】，无右孩子。【888】比【233】大，交换【233】与【888】。结果如下：

交换后，【233】无孩子节点，无需继续考虑【233】

2. 考虑【666】

其左右孩子中，【985】比【688】大。且【985】比【666】也大，交换【666】与【985】。结果如下：

交换后，【666】无孩子节点，无需继续考虑【666】

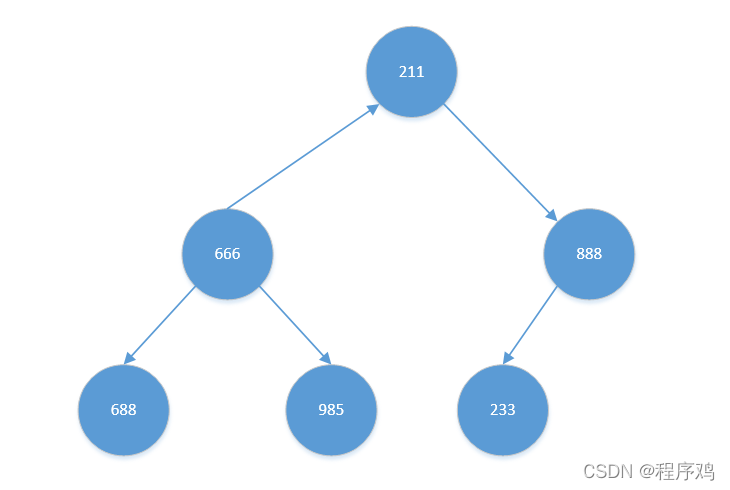
3. 考虑【211】

其左右孩子中，【985】比【888】大。且【985】比【211】也大，交换【211】与【985】。结果如下：

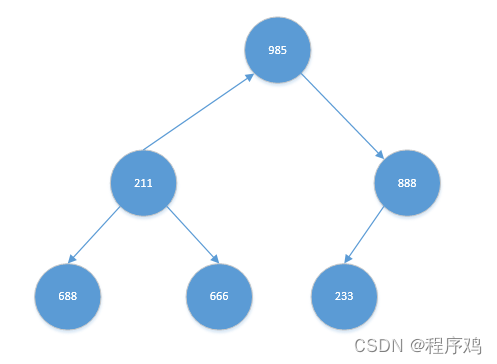
交换后，【211】有孩子节点。其左右孩子中，【688】比【666】大。且【688】比【211】也大，交换【211】与【688】。结果如下：

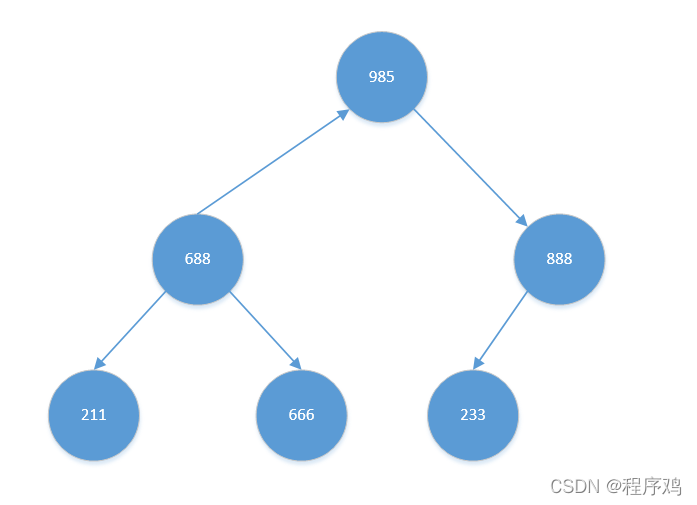
至此，已建立大根堆

交换堆顶元素与堆底元素，并重新调整大根堆

• 将堆顶元素【985】与堆底元素【233】交换。结果如下：
  

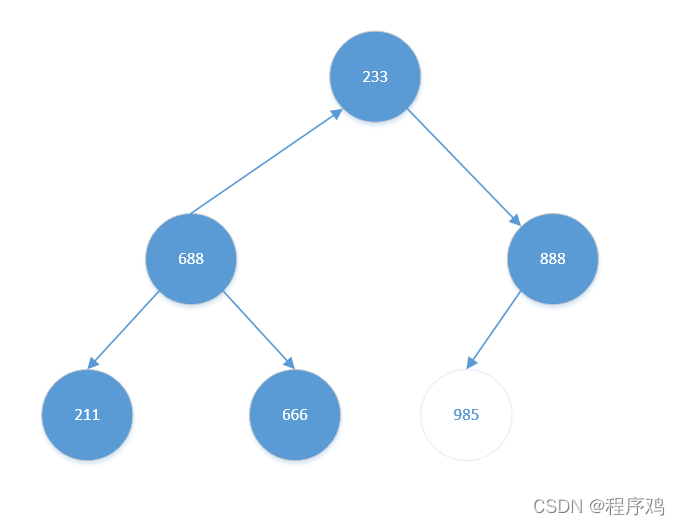
此时待排序元素（前5个）已不是大根堆，需要重新调整为大根堆

考虑堆顶元素【233】
其右孩子【888】比左孩子【688】更大。且【888】比【233】也大。交换【233】与【888】。结果如下：

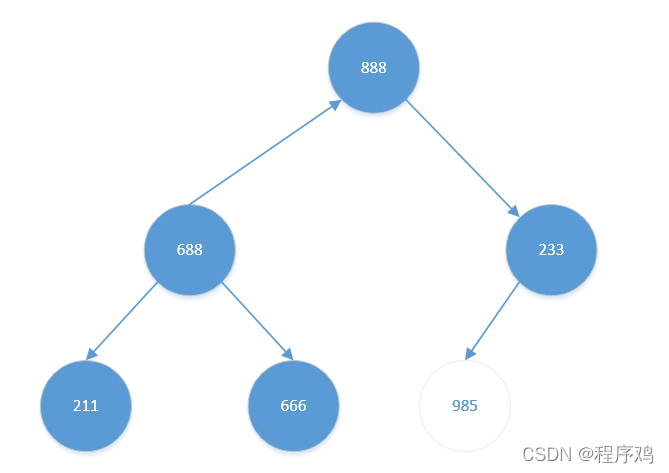
交换后，【233】无孩子节点（985为排好序的元素），无需继续考虑【233】

• 将堆顶元素【888】与堆底元素【666】交换。结果如下：
  

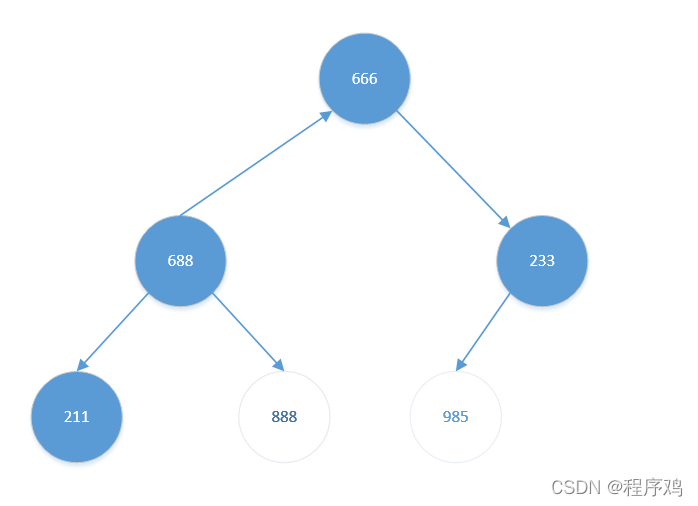
此时待排序元素（前4个）已不是大根堆，需要重新调整为大根堆

考虑堆顶元素【666】
其左孩子【688】比左孩子【233】更大。且【688】比【666】也大。交换【666】与【688】。结果如下：

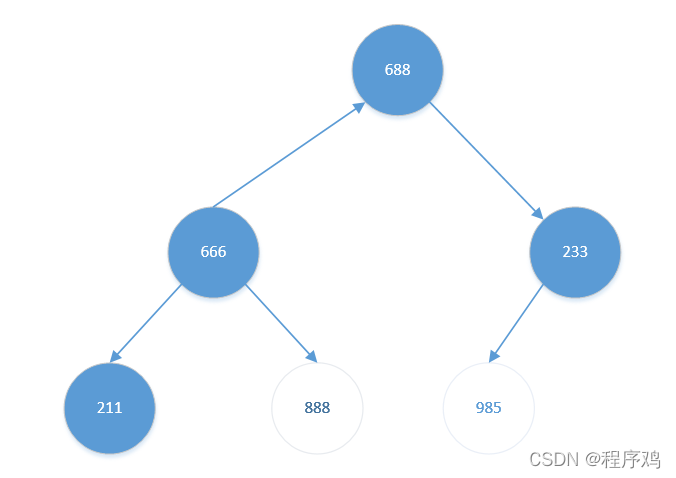
交换后，【666】有左孩子节点【211】（888为排好序的元素），但【211】比【666】小，不再进行调整

• 将堆顶元素【688】与堆底元素【211】交换。结果如下：
  

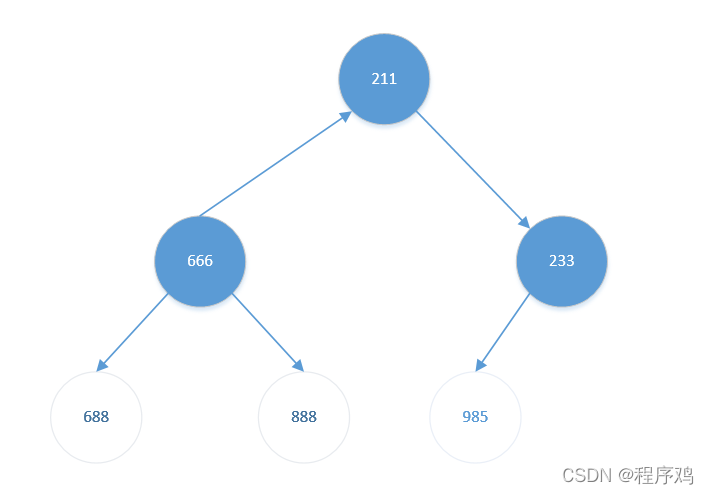
此时待排序元素（前3个）已不是大根堆，需要重新调整为大根堆

考虑堆顶元素【211】
其左孩子【666】比左孩子【233】更大。且【666】比【211】也大。交换【211】与【666】。结果如下：

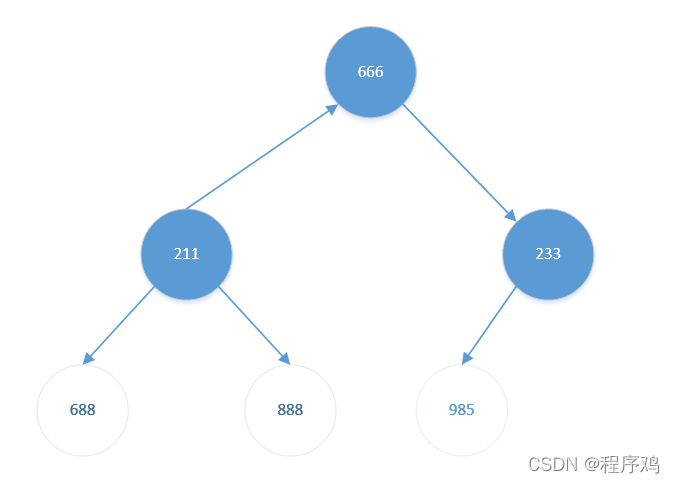
交换后，【211】无孩子节点（688、888为排好序的元素），无需继续考虑【211】

• 将堆顶元素【666】与堆底元素【233】交换。结果如下：
  

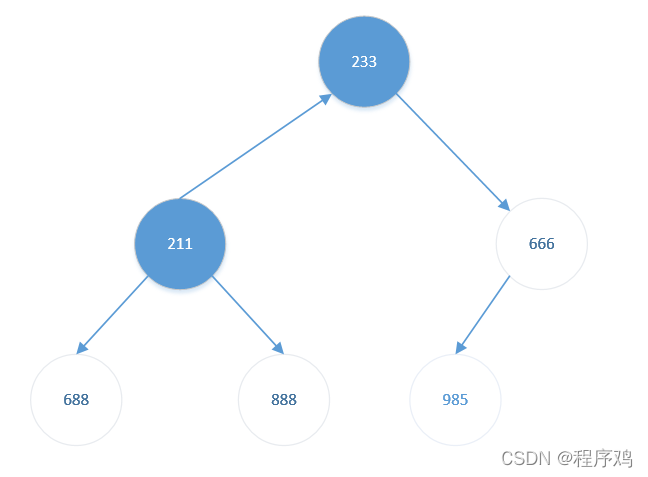
此时待排序元素（前2个）仍是大根堆，无需调整

• 将堆顶元素【233】与堆底元素【211】交换。结果如下：
  

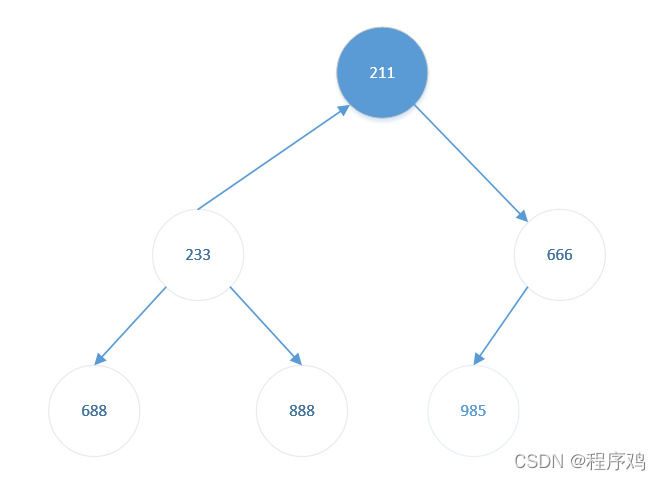
此时待排序元素（前1个）仍是大根堆，无需调整。

排序完成（升序），211<233<666<688<888<985

时间复杂度

建堆的时间复杂度

在调整堆时，每交换一次节点，最多比较关键字2次

• 比较1次：目标节点只有左孩子，无右孩子，将目标节点与其左孩子比较1下
• 比较2次：目标节点左右孩子均有，首先左右孩子先比较1下，然后大者再与目标节点比较1下

若目标节点在$x$层，树高为$h$，则调整时，目标节点最多交换$(h?x)$次，每次最多比较2次关键字，故$x$层节点的关键字对比次数不超过$2\times (h?x)$次

假设一颗完全二叉树，树高为h，最后一层节点无需进行调整
第1层共有1个节点，关键字对比次数最多为$1\times 2\times (h?1)$次
第2层共有2个节点，关键字对比次数最多为$2\times 2\times (h?2)$次
第h-1层共有2^h-2个节点，关键字对比次数最多$2^{h?2}\times 2\times 1$次
将整颗树调整为大根堆，关键字对比次数最多$1\times 2\times (h?1)+2\times 2\times (h?2)+...+2^{h?2}\times 2\times 1$次

处理上式为：${\sum }_{i=1}^{h?1}{2}^{i?1}\times 2\times (h?i)={\sum }_{i=1}^{h?1}{2}^i\times (h?i)$
由于n个节点的完全二叉树的高$h={\log }_{2}n+1$（向下取整）
$令j=h?i，则i=h?j。$原式$={\sum }_{j=h?1}^1{2}^{h?j}\times j={\sum }_{j={\log }_{2}n}^1{2}^{{\log }_{2}n+1?j}\times j={\sum }_{j={\log }_{2}n}^{1}n\times 2\times 2^{?j}\times j=2n\times {\sum }_{j={\log }_{2}n}^1{2}^{?j}\times j$

考虑$S_n={\sum }_{j=h}^1{2}^{?j}\times j={\sum }_{j=1}^h{2}^{?j}\times j=1\times \frac{1}{2}+2\times \frac{1}{4}+3\times \frac{1}{8}+...+h\times \frac{1}{2^h}$ ①
将$①\times \frac{1}{2}$ 得 $\frac{1}{2}{S}_n=1\times \frac{1}{4}+2\times \frac{1}{8}+...+(h?1)\times \frac{1}{2^h}+h\times \frac{1}{2^{h+1}}$ ②
使用错误相减法②-①得： $\frac{1}{2}{S}_n=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{2^h}?h\times \frac{1}{2^{h+1}}=\frac{\frac{1}{2}(1?\frac{1}{2^n})}{1?\frac{1}{2}}?h\times \frac{1}{2^{h+1}}=1?\frac{1}{2^n}?\frac{h}{2^{h+1}}$ ③
将$③\times 2$得：$S_n=2?\frac{1}{2^{h?1}}?\frac{h}{2^h}$④
很明显④式小于2即$S_n<2，所以2n\times {\sum }_{j={\log }_{2}n}^1{2}^{?j}\times j<4n$

建堆的时间复杂度为O(n)

交换堆顶底元素后重建堆的时间复杂度

每次将堆顶元素与堆底元素进行交换后，需要将剩余待排序元素重新建堆。此时处理的是堆顶元素，即根节点。根节点位于第一层，关键字最多比较次数为$2\times (h?1)$次。
上述过程共需进行n-1次（n为节点个数），故重建堆的总的关键字最多比较次数为$2\times (h?1)\times (n?1)=2{\log }_{2}n(n?1)$

重建堆的时间复杂度为O(nlogn)

堆排序的时间复杂度为O(nlogn)+O(n)=O(nlogn)

空间复杂度

整个排序过程，包括初建堆、交换顶底元素、重建堆，未用到其他多余的空间，主要进行比较与交换工作，所以空间复杂度是O(1)