problem
1143. Longest Common Subsequence
Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.
A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
- For example, “ace” is a subsequence of “abcde”.
A common subsequence of two strings is a subsequence that is common to both strings.
Example 1:
Input: text1 = "abcde", text2 = "ace"
Output: 3
Explanation: The longest common subsequence is "ace" and its length is 3.
Example 2:
Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.
Example 3:
Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.
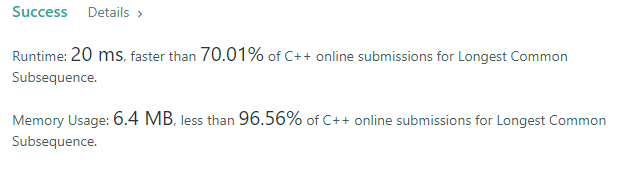
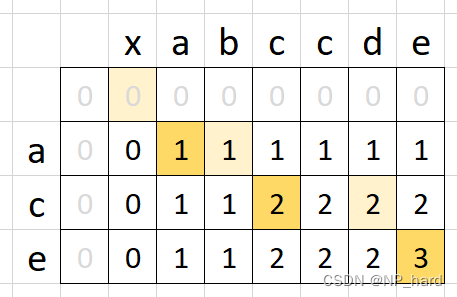
approach DP
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
vector<vector<int>> dp(text1.size()+1, vector<int>(text2.size()+1, 0));
for(int i=0; i<text1.size(); i++){
for(int j=0; j<text2.size(); j++){
if(text1[i] == text2[j]){
dp[i+1][j+1] = dp[i][j] + 1;
}else dp[i+1][j+1] = max(dp[i][j+1], dp[i+1][j]);
}
}
return dp[text1.size()][text2.size()];
}
};
approach shorter code
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
vector<vector<int>> dp(2, vector<int>(text2.size()+1, 0));
for(int i=0; i<text1.size(); i++)
for(int j=0; j<text2.size(); j++)
dp[(i+1)%2][j+1] = text1[i] == text2[j] ? dp[i%2][j] + 1 : max(dp[i%2][j+1], dp[(i+1)%2][j]);
return dp[text1.size()%2][text2.size()];
}
};
wrong approach
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
string small, big;
if(text1.size() > text2.size()){
small = text2, big = text1;
}else{
small = text1, big = text2;
}
int j = 0, pre = 0 , cnt = 0;
for(auto x : small){
for(; j<big.size(); j++){
if(big[j] == x){
cnt++;
pre = j + 1;
break;
}
}
if(j == big.size()){// not found
j = pre;
}
}
return cnt;
}
};