1. 代码分析
1.1 斜切处理
那对于之前“假想”斜切的实现,我们应该如何做呢?是否需要单独写一个比较方法呢?其实是没有必要的,大家应该还记得之前的比较规则:
设
任
意
两
个
端
点
坐
标
P
1
(
x
1
,
y
1
)
,
P
2
(
x
2
,
y
2
)
,
(
1
)
?
如
果
x
1
≠
x
2
,
则
我
们
正
常
比
较
x
坐
标
的
大
小
即
可
,
即
x
1
>
x
2
,
P
1
在
P
2
的
右
边
,
反
之
在
左
边
。
(
2
)
?
如
果
x
1
=
x
2
,
且
y
1
≠
y
2
,
我
们
则
比
较
y
坐
标
的
大
小
,
即
y
1
>
y
2
,
P
1
在
P
2
的
右
边
,
反
之
在
左
边
。
(
3
)
?
如
果
x
1
=
x
2
,
且
y
1
=
y
2
,
则
两
端
点
重
合
,
第
二
种
退
化
情
况
退
化
为
第
一
种
退
化
情
况
。
设任意两个端点坐标P_{1}(x_{1}, y_{1}),P_{2}(x_{2}, y_{2}),\newline(1)\,如果x_{1} \neq x_{2},则我们正常比较x坐标的大小即可,即x_{1} > x_{2},P_{1}在P_{2}的右边,反之在左边。\newline (2)\,如果x_{1} = x_{2},且y_{1} \neq y_{2},我们则比较y坐标的大小,即y_{1} > y_{2},P_{1}在P_{2}的右边,反之在 左边。\newline (3)\,如果x_{1} = x_{2},且y_{1} = y_{2},则两端点重合,第二种退化情况退化为第一种退化情况。
设任意两个端点坐标P1?(x1?,y1?),P2?(x2?,y2?),(1)如果x1??=x2?,则我们正常比较x坐标的大小即可,即x1?>x2?,P1?在P2?的右边,反之在左边。(2)如果x1?=x2?,且y1??=y2?,我们则比较y坐标的大小,即y1?>y2?,P1?在P2?的右边,反之在左边。(3)如果x1?=x2?,且y1?=y2?,则两端点重合,第二种退化情况退化为第一种退化情况。
不知道大家知道这个比较规则可以等价于一个什么比较常用的方法么?没错,其实就是按照x坐标进行升序排序:x坐标越大,端点越靠右,如果x坐标相同,则y坐标越大,端点越靠右,所以我们直接使用 Vectors.sortByX( p1, p2 ) 进行比较即可,无需实现任何新方法。
1.2 端点处理
当端点发生重合,处理方式和之前一样,无需做出任何更改。另一种情况,当端点落在线段上,我们需要在两处进行区分,第一个地方是在followSegment(),这里我们需要沿着邻居梯形来查找新插入线段横跨的梯形区域,所以需要进行修改。思路也不难,先区分rightP落在右端点的上方,下方,还是在线段上,这里我们使用toleft测试进行判断。同时,这里必须保证输入线段右端点一定在左端点右边,否则算法会出错:
// j <- 0;
// while q lies to the right of rightP(Dj).
// D0.rightP.isRight( q ) -- no shear transformation.
// imagine that we applied shear transformation to the map.
while ( Vectors.sortByX( D0.rightP, q ) < 0 ) {
double res = Triangles.areaTwo( p, q, D0.rightP );
// if rightP(Dj) lies on si
if ( MyMath.isEqualZero( res ) ) {
D0 = followSegment( D0, q );
}
// do if rightP(Dj) lies above si
else if ( MyMath.isPositive( res ) ) {
// then Let Dj+1 be the lower right neighbor of Dj.
D0 = D0.lowerRightNeighbor;
}
else {
// else Let Dj+1 be the upper right neighbor of Dj.
D0 = D0.upperRightNeighbor;
}
// j <- j+1
assert D0 != null : l;
Ds.add( D0.vertex );
}
接下来就是当右端点落在线段上的情况,代码如下:
private static
Trapezoid followSegment( Trapezoid D0, Vector q ) {
Trapezoid upperRight = D0.upperRightNeighbor;
Trapezoid lowerRight = D0.lowerRightNeighbor;
// rightP(Dj) is P node of sj
if ( upperRight != null && lowerRight != null ) {
// endpoint of si ( q ) lies above sj
if ( D0.rightP.isAbove( q ) )
D0 = D0.upperRightNeighbor;
else
D0 = D0.lowerRightNeighbor;
}
// rightP(Dj) is Q node of sj
else if ( upperRight != null )
D0 = D0.upperRightNeighbor;
else if ( lowerRight != null )
D0 = D0.lowerRightNeighbor;
// impossible both are null.
else assert false;
return D0;
}
判断方法是根据右邻居来判别的,根据我们在上一节 2.3 变幻莫测的端点 中,我们可以通过观察发现:
(1)当Si覆盖Sj左端点,那么D0一定右两个右邻居,并且如果Si的右端点在Sj的上方,Si横跨upperRight梯形邻居,反之横跨lowerRight梯形邻居;
(2)当Si覆盖Sj右端点,那么D0一定只有一个右邻居,并且如果upperRight != null,则Si横跨它,反之则横跨lowerRight梯形邻居;
利用上面的关系,我们就能写出相应的代码。下图说明了上述结论:
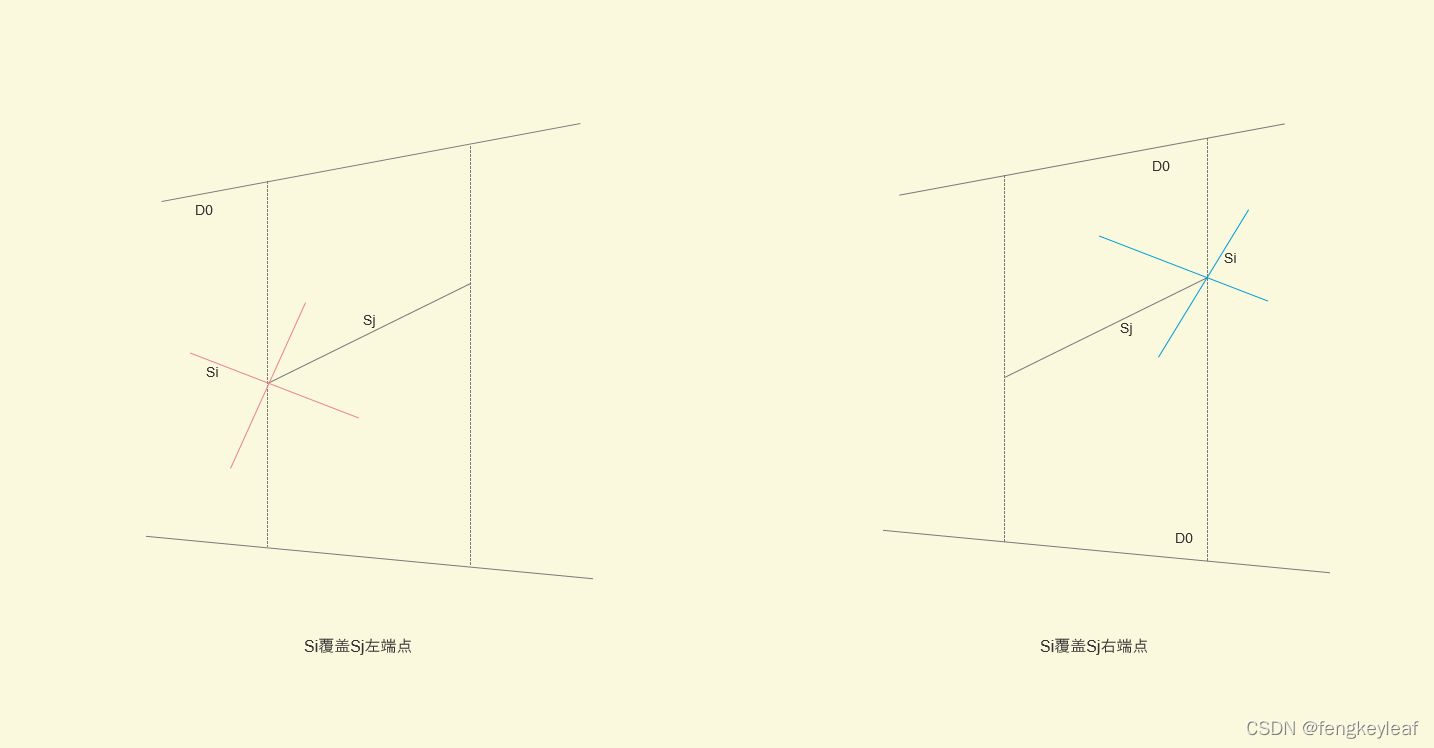
同样,在trim()(位于TrapezoidalMap.java中)中判断是合并上梯形,还是下梯形,我们使用的代码逻辑几乎一模一样,这里就略过,有兴趣的童鞋可以参考项目代码。
1.3 虚梯形
虚梯形(Zero-area trapezoid)和一般梯形的数据结构都是一样的,只是它的面积为零,所以我们没有必要为它更改梯形的数据结构代码,但是在可视化阶段,把梯形转换成DCEL进行绘图,虚梯形还能正常显示嘛?答案是没有问题的,只是在可视化结果中,虚梯形是不可见的,或者说退化成了一个条竖线。下图展示了包含垂直线,且它们首尾相连的梯形图:

大家可以看到,本来两条垂直经过“斜切”后会形成虚梯形,但是可视化结果中它们都退化成了竖线。最后我们需要更改一下搜索结构中查询点的逻辑,一共有三种情形:1)落在端点上;2)落在线段上;3)落在梯形上,我们只要根据搜索结构进行查找即可,代码不难,大家可以自己参考项目代码,这里就不再赘述了。
2. 案例展示
到此,我们就把点定位处理退化情况的代码给大家讲解完毕了,大家可能已经注意到了,和之前较为繁琐的分析思路不一样,这里的代码实现非常的简单,都是复用以前的代码结构和逻辑。所以从这里,大家应该能感受思路分析对优雅代码的重要性,只要逻辑清晰,可以大幅简化代码量。
最后,这里给大家展示一下使用完善后的点定位算法,处理教材上一个类多边形的输入案例1,并进行空间点查找:
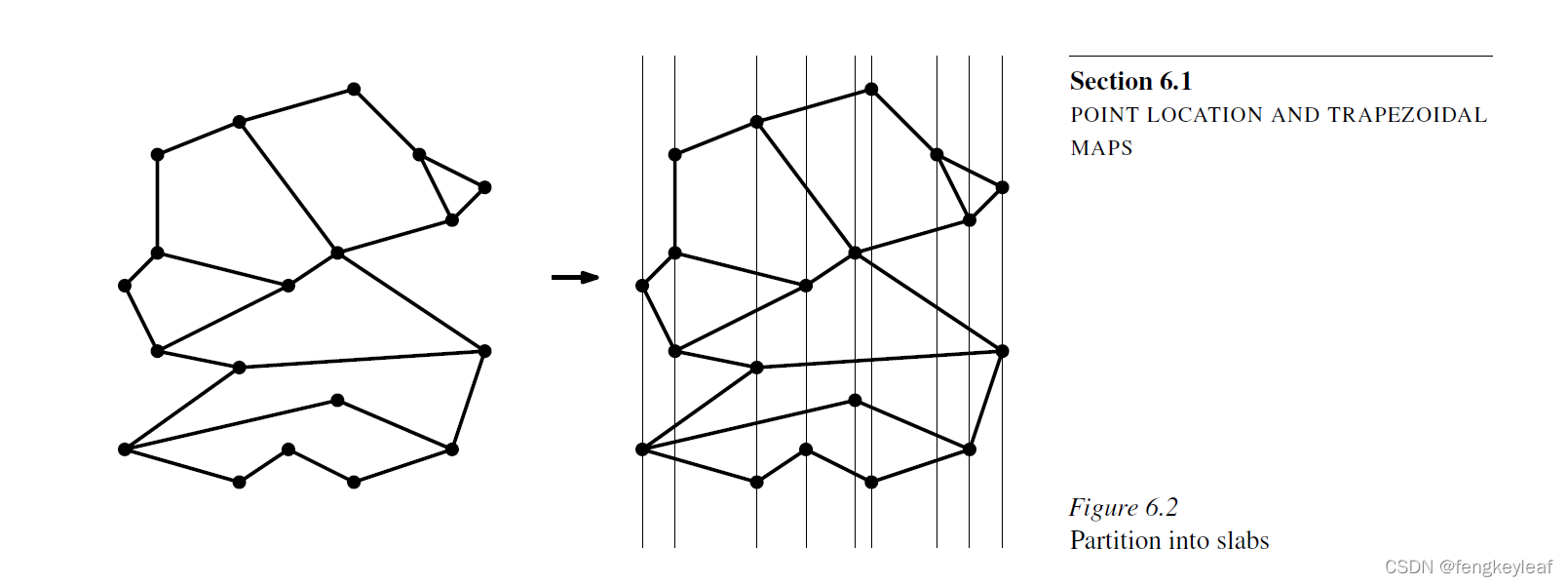
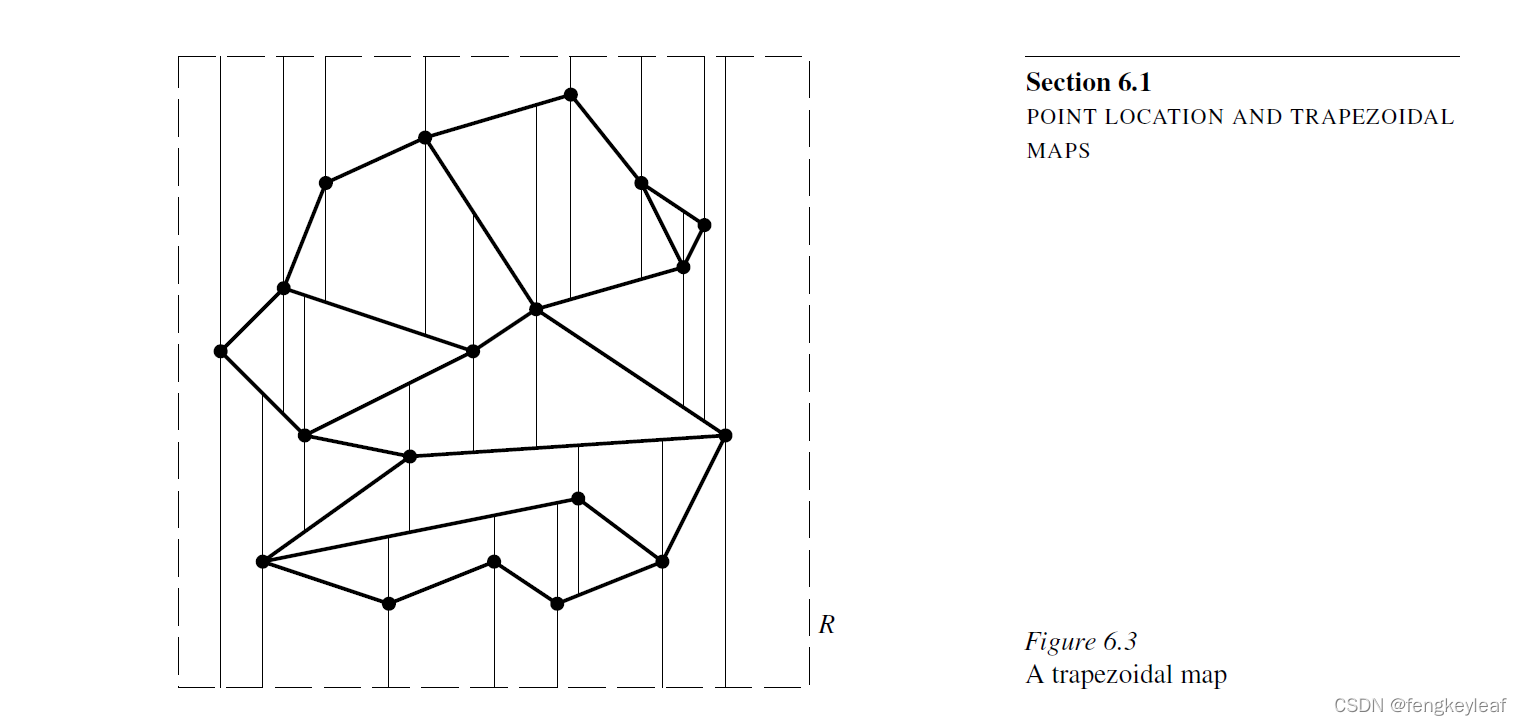
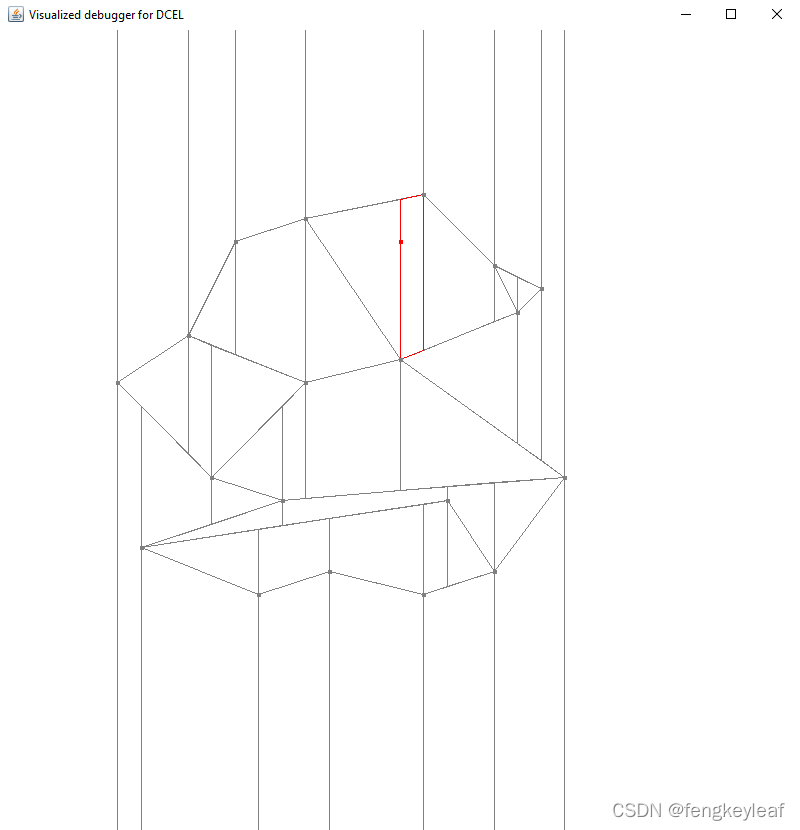
红色点为查询点,红色区域为查询点所在的梯形。接下来,我们将正式进入到Voronoi图算法章节之中,但在进入到算法讲解之前,我们先来看看塞尔达野炊背后的计算几何,或者说塞尔达地图和Voronoi图的联系,它们两者究竟又有怎样的联系呢?
上一节:点定位:处理退化情况
下一节:Voronoi图:塞尔达背后的计算几何
系列汇总:塞尔达和计算几何 | Voronoi图详解文章汇总(含代码)
4. 附录:代码
4.1 算法
| Description | Entry method\File |
|---|---|
| Build trapezoidal Map and search structure( 创建梯形图和二分搜索结构 ) | BoundingBox trapezoidalMap( List lines ) |
| Point Locatoin( 点定位 ) | public SearchVertex get( Vector p ) |
| Program ( including visualization, 可视化程序 ) | Programming Assignment 3 - Trapezoidal Map and Planar Point Location |
4.2 数据结构
| Description | Entry File/Package |
|---|---|
| Trapezoidal Map( 梯形图 ) | public class Trapezoid |
| Search Structure( Tree-like DAG, 二分搜索结构,树状DAG ) | public class SearchStructure |
5. 参考资料
- Computational Geometry: Algorithms and Applications
- 计算几何 ?? 算法与应用, 邓俊辉译,清华大学出版社
6. 免责声明
※ 本文之中如有错误和不准确的地方,欢迎大家指正哒~
※ 此项目仅用于学习交流,请不要用于任何形式的商用用途,谢谢呢;
