1.基础快排

快排也是交换排序的一种

基本思路：

1. 从待排序区间选择一个数，作为基准值(pivot)；

2. Partition: 遍历整个待排序区间，将比基准值小的（可以包含相等的）放到基准值的左边，将比基准值大的（可以包含相等的）放到基准值的右边；

3. 采用分治思想，对左右两个小区间按照同样的方式处理，直到小区间的长度 == 1，代表已经有序，或者小区间的长度 == 0，代表没有数据。?

1.1递归代码实现

    /**
     * 基础版快速选择排序递归版
     * @param arr
     */
    public static void quilkSort1(int[] arr){
        int n = arr.length;
        quilkSort1Recursion(arr,0,n - 1);
    }

//    对[left,right]范围内的数组进行快排,分区点默认选第一个
    private static void quilkSort1Recursion(int[] arr, int left, int right) {
//        当区间元素小于15时，直接使用插入排序
        if(right - left <= 15){
            insertHelpMerge(arr,left,right);
            return;
        }
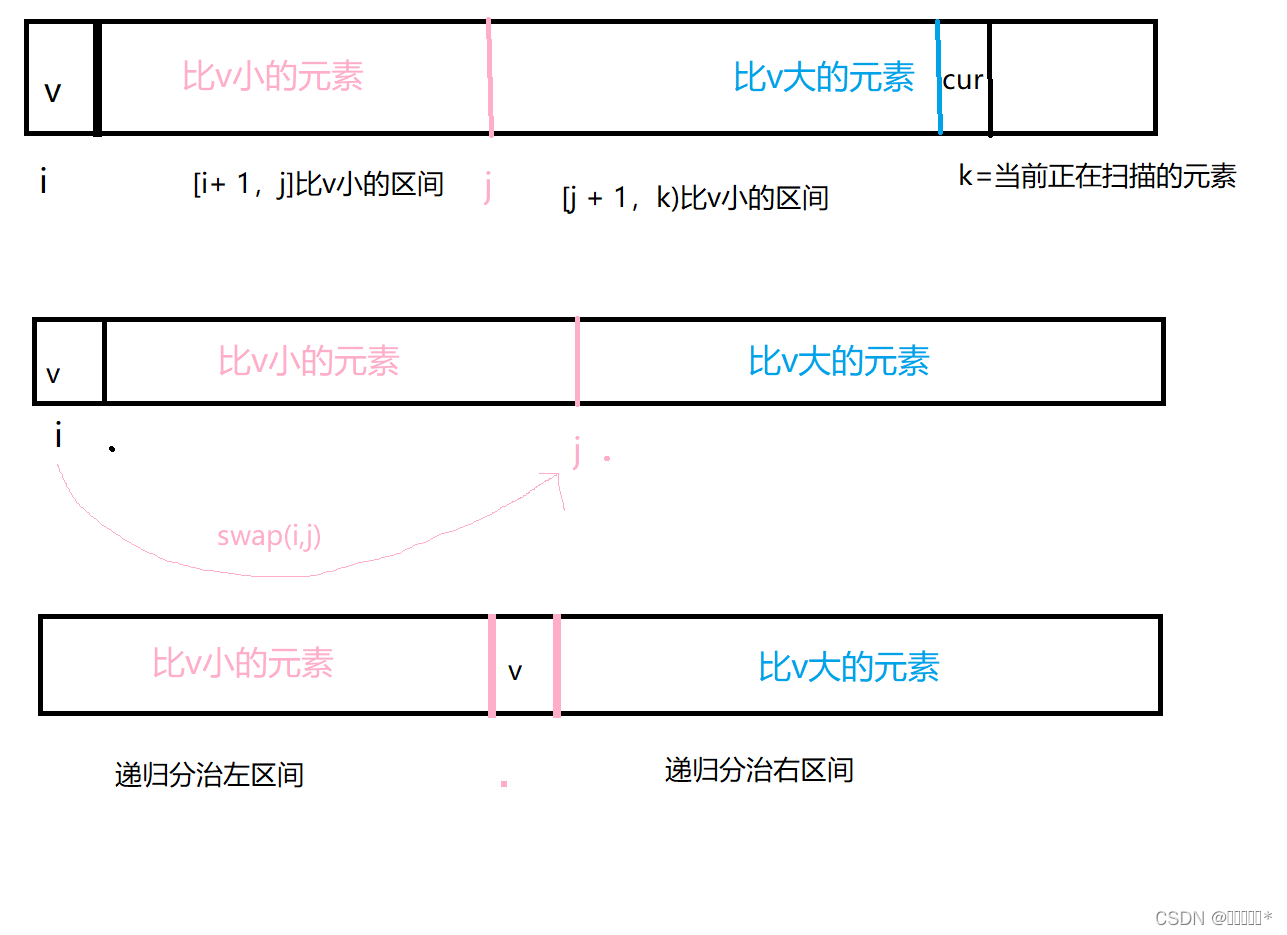
        int v = arr[left];
//        [left + 1,j]是小于v的区间
        int j = left;
//        [j + 1,k)是大于v的区间
        int k = left + 1;
        while (k <= right){
//            扫描到的元素比v大
            if(arr[k] >= v){
                k ++;
            }else {
//            扫描到的元素比v小
                swap(arr,k,j + 1);
                j ++;
                k ++;
            }
        }
//        此时，j指示的就是最后一个比v小的元素
        swap(arr,left,j);
//        递归左区间
        quilkSort1Recursion(arr,left,j - 1);
//        递归右区间
        quilkSort1Recursion(arr,j + 1,right);
    }

1.2非递归代码实现

非递归法借助栈，记录每次区间的开始结束位置，当开始结束位置区间元素小于等于1时，说明区间快排完毕

    /**
     * 基础快排，非递归写法,借助栈实现
     * @param arr
     */
    public static void quickSort2NoRecursion(int[] arr){
        Deque<Integer> stack = new LinkedList<>();
        int n = arr.length;
        int l = 0;
        int r = arr.length - 1;
        stack.push(r);
        stack.push(l);
        while (!stack.isEmpty()){
            int left = stack.pop();
            int right = stack.pop();
//            左大于等于右，说明区间只有一个或无元素，边界不用处理
            if(left >= right){
                continue;
            }
//            否则对该区间快排
            int p = quilk(arr,left,right);
//            将右区间结束开始位置入栈
            stack.push(right);
            stack.push(p + 1);
//            对左区间结束开始位置入栈
            stack.push(p - 1);
            stack.push(left);
        }
    }
//    对[left,right]范围内的数组进行快排,并返回分区点，基准值默认选第一个
    private static int quilk(int[] arr, int left, int right) {
        int v = arr[left];
//        [left + 1,j]是小于v的区间
        int j = left;
//        [j + 1,k)是大于v的区间
        int k = left + 1;
        while (k <= right){
//            扫描到的元素比v大
            if(arr[k] >= v){
                k ++;
            }else {
//            扫描到的元素比v小
                swap(arr,k,j + 1);
                j ++;
                k ++;
            }
        }
//        此时，j指示的就是最后一个比v小的元素
        swap(arr,left,j);
        return j;
    }

2.快排优化问题之——数据近乎有序

当数组近乎有序时，如果还是默认区间的第一个值为基准值，会导致后续分治求区中，左右两个区间严重不平衡，本来二叉树的结构反而退化为了链表的结构，时间复杂度反而由

O（n logn)退化为了O（n^2)

所以，为了避免这种情况，我们要作出优化，优化方法就是围绕着挑选基准值来优化

2.1基准值随机选择

在每次的区间里进行快排时，随机选择一个数作为基准值

代码实现：

   /**
     * 随机数作为基准值的快排
     * @param arr
     */
    public static void quickSort3(int[] arr){
        quickRandom(arr,0,arr.length - 1);
    }

    private static void quickRandom(int[] arr, int left, int right) {
        if(left >= right){
            return;
        }
//        区间范围内的随机索引下标
        int randomIndex = random.nextInt(left,right);
//       交换随机元素和最左侧元素
        swap(arr,left,randomIndex);
//        此时最左侧为基准就是随机元素为基准
        int v = arr[left];
        int j = left;
        for (int k = j + 1; k <= right; k++) {
            if(arr[k] < v){
                swap(arr,k,j + 1);
                j ++;
            }
        }
        swap(arr,j,left);
        quickRandom(arr,left,j - 1);
        quickRandom(arr,j + 1,right);
    }

2.2基准值三数取中

比较区间最左，最右，和中间元素，选择大小为中间的那个元素作为基准元素

    /**
     * 三数取中法选择基准
     * @param arr
     */
    public static void quickSort4(int[] arr){
        quickMid(arr,0,arr.length - 1);
    }

    private static void quickMid(int[] arr, int left, int right) {
        if(left >= right) {
            return;
        }
        int mid = left + (right - left) >> 1;
//        三数取中
        int i = mid(arr,left,mid,right);
//        交换基准位置
        swap(arr,left,i);
        int v = arr[left];
        int j = left;
        for (int k = j + 1; k <= right; k++) {
            if(arr[k] < v){
                swap(arr,j + 1,k);
                j ++;
            }
        }
        swap(arr,j,left);
        quickMid(arr,left,j - 1);
        quickMid(arr,j + 1,right);
    }
//    返回中间元素的索引下标
    public static int mid(int[] arr,int l,int m,int r){
        if(arr[l] >= arr[m] && arr[l] <= arr[r] || arr[l] <= arr[m] && arr[l] >= arr[r]){
            return l;
        }else if(arr[m] >= arr[l] && arr[m] <= arr[r] || arr[m] <= arr[l] && arr[m] >= arr[r]){
            return m;
        }else{
            return r;
        }
    }

3.快排优化问题之——重复元素过多

当数组重复元素过多时，不论把相等的元素放在哪一边，都会导致分区严重不平衡，时间复杂度又退化为O（n^2)，所以如果数组重复元素过多，我们也可以进行优化；

优化方式主要有两种：2路快排和3路快排

3.1二路快排

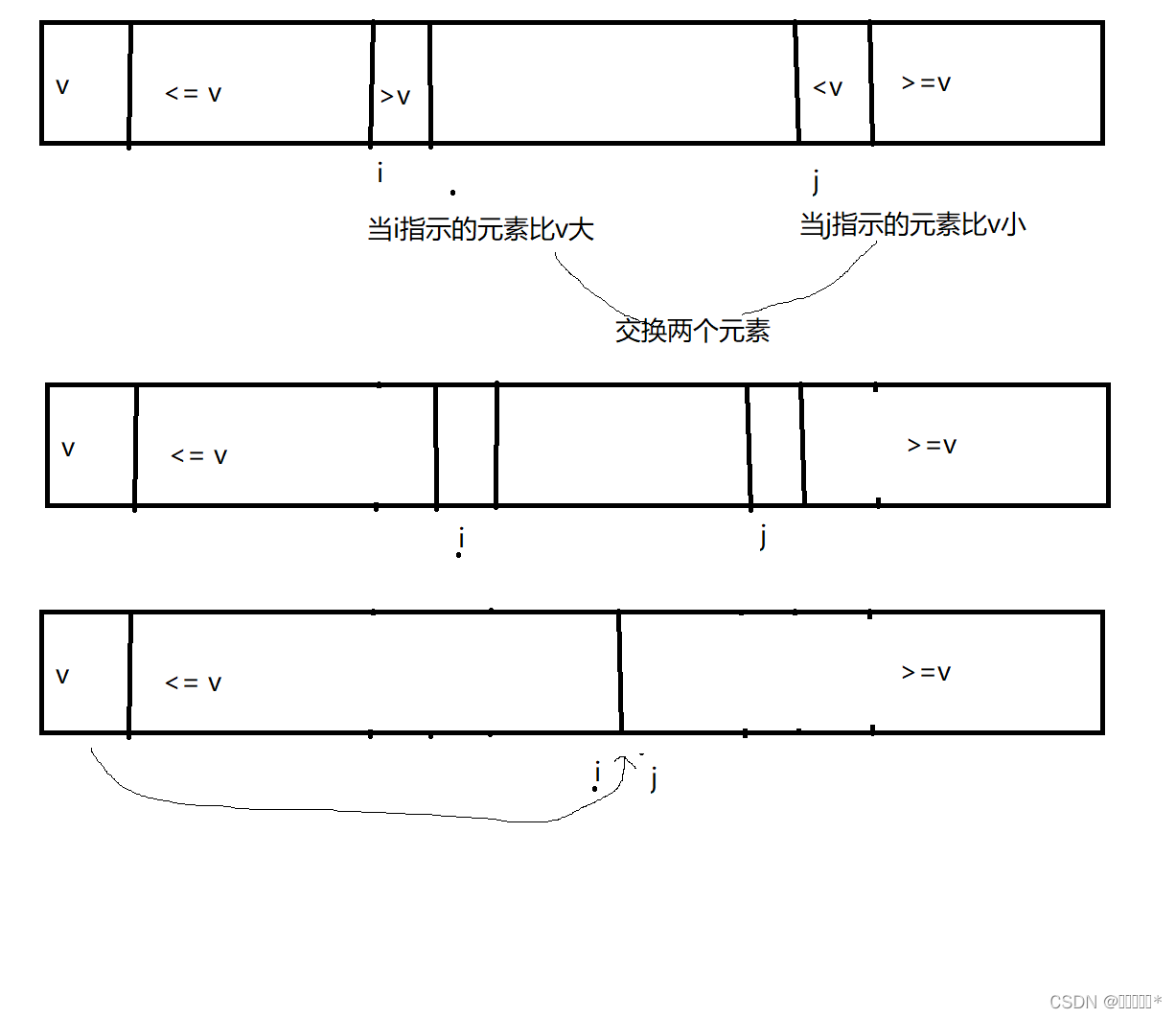
二路快排：

两个指针，基准元素为v；

一个指针i从前向后遍历，一个指针j从后向前遍历，i走到比v大的元素，停止，j走到比v小的元素，停止，然后交换这两个元素的位置

代码实现：

    /**
     * 二路快排
     *
     * @param arr
     */
    public static void quickSortTwo(int[] arr) {
        quickTwo(arr, 0, arr.length - 1);
    }

    private static void quickTwo(int[] arr, int left, int right) {
        if(left >= right){
            return;
        }
//        避免近乎有序，基准位置随机化
        int randomIdex = random.nextInt(left, right);
        swap(arr, randomIdex, left);
        int v = arr[left];
//        i是左指针
        int i = left + 1;
//        j是右指针
        int j = right;
//        要取等，有可能一开始i就和j相等（区间只有2个元素时），所以还要进循环里去比较和v的大小，如5 8两个元素，5为基准，8无需交换
        while (i <= j) {
            while (i <= j && arr[i] < v) {
                i++;
            }
//            此时，i指示第一个大于v的数
            while ( i <= j && arr[j] > v) {
                j--;
            }
            //            此时，J指示第一个小于v的数
            if(i >= j){
                break;
            }
//            交换i和j
            swap(arr, i, j);
            i++;
            j--;
        }
//        当遍历完,j指示最后一个小于等于v的元素
        swap(arr,left,j);
//        递归左、右
        quickTwo(arr,left,j - 1);
        quickTwo(arr,j + 1,right);

    }

上面实现的二路快排是基于交换左右元素实现的，常见的还有一种做法，基本思路和上述一致，只是不再进行交换元素，而是直接赋值元素覆盖?，也叫挖坑再填坑

?

?

代码：

3.2三路快排

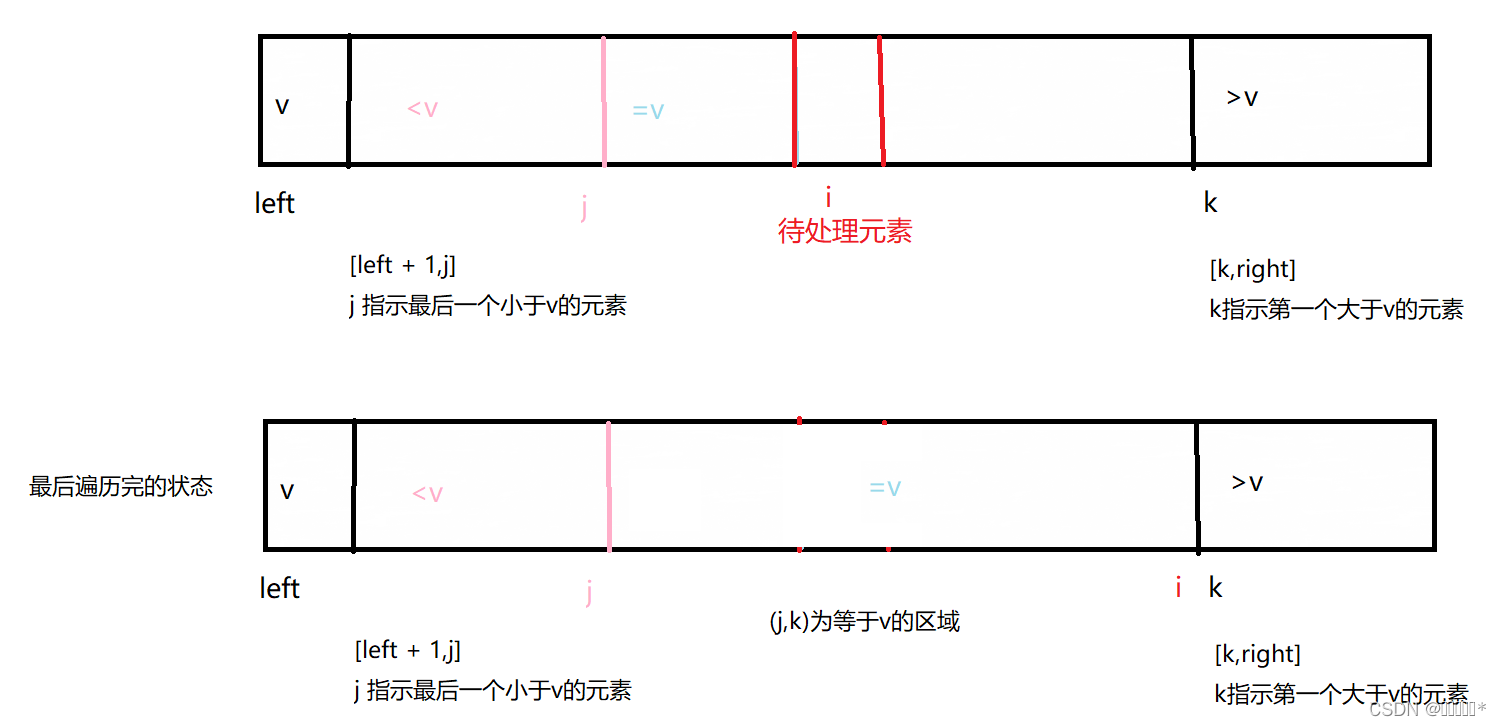
2路快排，实则还是将相等的元素分入不同的区间去进行再次排序，左右移来移去，做了很多无用功，故而，我们想到，可以再加一个空间区域，里面存放等于基准元素的数据，这就是三路快排，<v 的区域，等于 v 的区域，以及 >v 的区域；

分治分区时，只需继续快排左边 <v 和右边 >v的区间即可，对于中间相等区域，无需再操作

对于待处理元素arr[i]:

（1）arr[i] < v

swap(j + 1,i)? ? ? ?j ++? ?,? ? ? i ++?

（2）arr[i] = v

i++

（3）arr[i] > v

swap(i,k - 1)? ?k --

【边界】i >= k

代码实现：

  /**
     * 三路快排
     * @param arr
     */
    public static void quickSortThree(int[] arr){
        quickThree(arr,0,arr.length - 1);
    }

    private static void quickThree(int[] arr, int left, int right) {
        if(left >= right){
            return;
        }
//        基准元素随机化
        int randomIndex = random.nextInt(left,right);
        swap(arr,left,randomIndex);
        int v = arr[left];
//        [left + 1,j] <v的区间，(j,k) =v 的区间，[k,right] >v的区间
        int j = left;
        int k = right + 1;
        int i = j + 1;
        while(i < k){
//            当比v小时
            if(arr[i] < v){
                swap(arr,i,j + 1);
                j ++;
                i ++;
            }else if(arr[i] == v){
//                等于v时，i++
                i++;
            }else{
//                大于v
                swap(arr,i,k - 1);
                k --;
            }
        }
//        此时已遍历完，交换基准位置
        swap(arr,left,j);
//        递归左右区间
        quickThree(arr,left,j - 1);
        quickThree(arr,k,right);
    }