[数据结构与算法]回溯法求N皇后问题

回溯法求N皇后问题

搜索解的过程如图

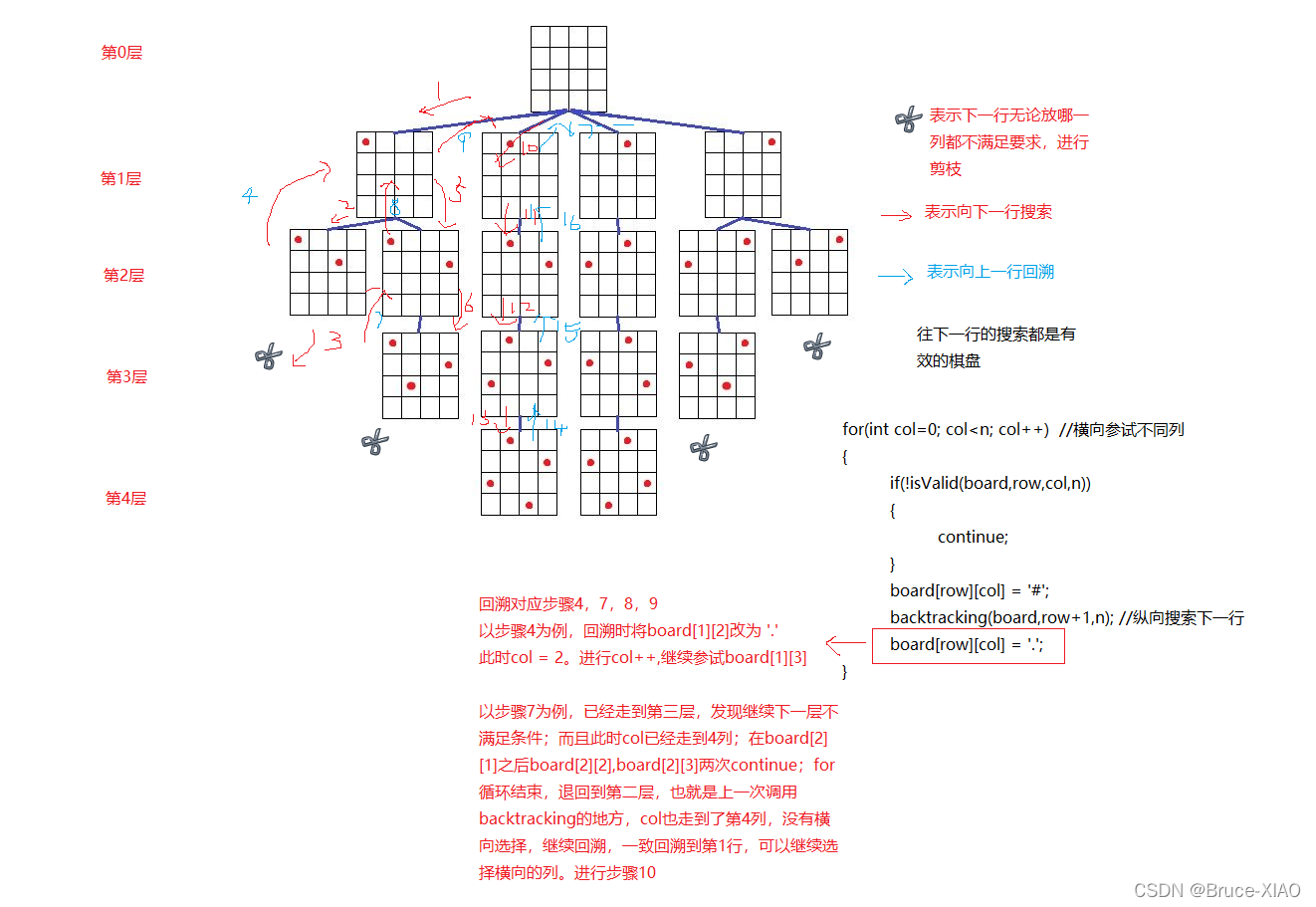
回溯法包括两个过程，DFS&回溯，DFS搜索是在满足条件时往下一层，回溯是在将一层的选择尝试完成之后不满足条件或者达到最底层，才回到上一层。类似于一种暴力的搜索算法。

在每一层会有多个选择，用for 横向尝试每一列，isValid函数判断（row,col）的放置是否合法，实际上是控制是否继续往下一层搜索，做剪枝优化。合法的位置即是调用backtraking函数的入口，继续往下一层搜索。

回溯返回的时候就是上一层函数入口时的状态, 所处的row和col，如果col小于总列数，可以继续横向尝试下一列。

#include<iostream>
#include<vector> 
using namespace std;


int ans = 0;
void backtracking(vector<vector<char>> &board,int row,int n);
bool isValid(vector<vector<char>> &board,int row,int col,int n);

int solveNQueens(int n)
{
	vector<vector<char>> board(n,vector<char>(n,'.')); 
	backtracking(board,0,n);
	return ans;
}

void backtracking(vector<vector<char>> &board,int row,int n)
{
	if(row==n)
	{
		ans += 1;
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<n;j++)
			{
				putchar(board[i][j]);
				putchar(' ');
			}
			cout << endl;
		}
		cout << endl;
		return;
	}
	for(int col=0; col<n; col++)  //横向尝试不同列 
	{
		if(!isValid(board,row,col,n))  
		{
			continue;
		}
		board[row][col] = '#';
		backtracking(board,row+1,n); //纵向搜索下一行 
		board[row][col] = '.';
	}
}

bool isValid(vector<vector<char>> &board,int row,int col,int n)
{
	//左上方
	for(int i=row-1,j=col-1; i>=0 && j>=0; i--,j--)
	{
		if(board[i][j] == '#')
		{
			return false;
		}
	} 
	//正上方 
	for(int i=0;i<row;i++)
	{
		if(board[i][col] == '#')
		{
			return false; 
		}
	}
	//右上方
	for(int i=row-1,j=col+1;i>=0&&j<n; i--,j++)
	{
		if(board[i][j] == '#')
		{
			return false;
		}
	} 
	return true;
}

int main()
{
	int n = 0;
	cin >> n;
	int ans = solveNQueens(n);
	cout << ans << endl;
	
	return 0;	
} 

运行结果

参考