今日刷题内容
简单循环
(题目链接就不贴了,昨天的文章竟然给我警告了,说我链接太多,真无语)
剑指 Offer 64. 求1+2+…+n
这个题,看题目就知道很水
public int sumNums(int n) {
int sum = 0;
for(int i=1;i<=n;i++){
sum+=i;
}
return sum;
}
虽然是循环 但是还是用递归来一下吧
public int sumNums(int n) {
if(n==0){
return 0;
}
return n+ sumNums(n-1);
}
231. 2 的幂
题目要求:给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。如果存在一个整数 x 使得 n == 2^x ,则认为 n 是 2 的幂次方。
思路:一开始看到这道题,立马想到的是拿这个数不断去除二,但是仔细一想,java的除法运算对于除不尽的数,结果是会向下取整的 所以这样做是不行的,所以要给它加上一个限定条件 可以被二整除的才除二,
不能被整除的也肯定不是2的幂
public boolean isPowerOfTwo(int n) {
if (n <= 0) return false;
while (n % 2 == 0) n /= 2;
return n == 1;
}

public bool isPowerOfTwo(int n){
int i;
unsigned int k = 1; // (1)
if(n <= 0) {
return false; // (2)
}
if(n == 1) {
return true; // (3)
}
for(i = 1; i <= 31; ++i) {
k *= 2; // (4)
if(k == n) {
return true; // (5)
}
}
return false;
}
然后就是位运算的解法(说实话,看了大佬的代码可以懂,但是就是想不出来)
大佬:fengziL
题解链接:https://leetcode-cn.com/problems/power-of-two/solution/5chong-jie-fa-ni-ying-gai-bei-xia-de-wei-6x9m/
解法1(相当于乘法)
通过左位移操作,列举出 int 型内的全部2的幂次方
public boolean isPowerOfTwo(int n) {
if (!n) return false;
for (int i = 1, sub = 1; i < 32; ++i, sub <<= 1)
if (sub == n) return true;
return false;
}
解法2(相当于除法)
通过右位操作,把n做2的幂次方的逆逻辑
public boolean isPowerOfTwo(int n) {
if (!n) return n;
while (n % 2 == 0) n >>= 1;
return n == 1;
}
解法3
利用上面掉到的常用位操作:
n & -n 得到最低位的 1 的位置
再和 n ^
如果 n 只有一个1,那么 n ^ (n & -n) 就只可能是0,要么非0
public boolean isPowerOfTwo(int n) {
return n > 0 && (n ^ (n & -n)) == 0;
}
解法4
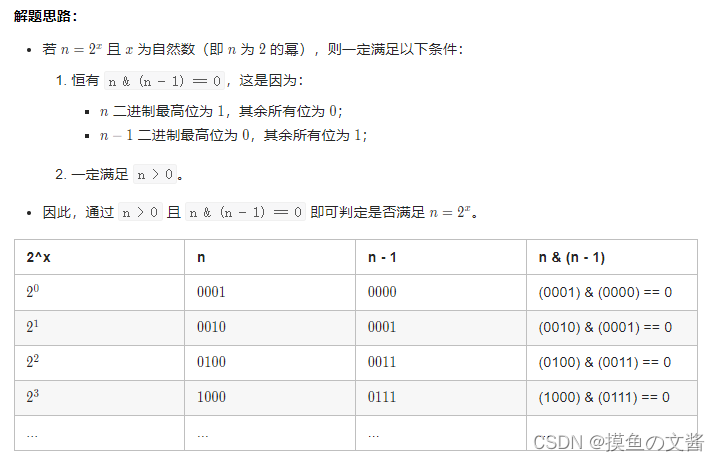
直接利用常用方法 n & (n - 1) 去除最低位的1。
如果 n 的二进行里面只有一个1,那么去掉最低位的1,就只可能是0,要么非0
public boolean isPowerOfTwo(int n) {
return n > 0 && (n & (n - 1)) == 0;
}
上面4种解法的本质,其实就是求出32个bit位里面有几个1,有点类似于JAVA里面的
public boolean isPowerOfTwo(int n) {
return n>0 && Integer.bitCount(n) == 1;
}
解法5,特化解法
传入的参数 n 为 int 类型
也就是 -2^31 <= n < 2^31
如果 n 为 2 的幂次方的话一定是:
[1, 2^30] 双闭区间
把 n 作为除数, 2^30 作为被除数,那么,如果 n 是 2 的幂次方的话,余数肯定为0
public boolean isPowerOfTwo(int n) {
return n > 0 && (1 << 30) % n == 0;
}
326. 3 的幂
给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false 。
整数 n 是 3 的幂次方需满足:存在整数 x 使得 n == 3^x
我们不断地将 n 除以 3,直到 n=1。如果此过程中 n 无法被 3 整除,就说明 n 不是 3 的幂。
思路1:和上一题相似
public boolean isPowerOfThree(int n) {
while (n != 0 && n % 3 == 0) {
n /= 3;
}
return n == 1;
}
public boolean isPowerOfThree(int n) {
int i;
int k = 1;
if(n <= 0) {
return false;
}
if(n == 1) {
return true;
}
for(i = 1; i <= 20; ++i) { // (1)
k *= 3; // (2)
if(k == n) {
return true;
}
}
return false;
}
342. 4的幂
给定一个整数,写一个函数来判断它是否是 4 的幂次方。如果是,返回 true ;否则,返回 false 。
整数 n 是 4 的幂次方需满足:存在整数 x 使得 n == 4^x
public boolean isPowerOfFour(int n) {
while (n != 0 && n % 4 == 0) {
n /= 4;
}
return n == 1;
}
public boolean isPowerOfFour(int n){
int i;
int k = 1;
if(n <= 0) {
return false;
}
if(n == 1) {
return true;
}
for(i = 1; i <= 15; ++i) { // (1)
k *= 4; // (2)
if(k == n) {
return true;
}
}
return false;
}
1492. n 的第 k 个因子
给你两个正整数 n 和 k 。如果正整数 i 满足 n % i == 0 ,那么我们就说正整数 i 是整数 n 的因子。
考虑整数 n 的所有因子,将它们 升序排列 。请你返回第 k 个因子。如果 n 的因子数少于 k ,请你返回 -1 。
思路:要的是从小到大排序的因子,那咱就给他从小到大去遍历,是因子就计数加一,直到等于时输出
public int kthFactor(int n, int k) {
int count = 0;
for (int num = 1; num <= n; num++) {
if (n % num == 0) {
++count;
if (count == k) {
return num;
}
}
}
return -1;
}
想想这个思路其实还可以优化,可以减少遍历的范围,如果 n=1000,那么从 501 开始到 999 结束,这些数都不是 n 的因子
public int kthFactor(int n, int k) {
int count = 0, factor;
for (factor = 1; factor * factor <= n; ++factor) {
if (n % factor == 0) {
++count;
if (count == k) {
return factor;
}
}
}
--factor;
if (factor * factor == n) {
--factor;
}
for (; factor > 0; --factor) {
if (n % factor == 0) {
++count;
if (count == k) {
return n / factor;
}
}
}
return -1;
}
367. 有效的完全平方数
题目要求:给定一个 正整数 num ,编写一个函数,如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
思路:最简单暴力的解法–从1开始给他遍历,拿每个数的平方结果去和给定数字比较,有相同的放回true,遍历结束还没有就返回false
public boolean isPerfectSquare(int num) {
for(int i=1;i<=(num + 1)/2;i++){
if(i * i == num){
return true;
}
}
return false;
}
虽然是过了,但是这个时间消耗也太长了吧,想想还有没有更巧妙的方法
于是我想起了在某个范围内去找一个数,这范围内的数还是有序,那不就是给二分查找准备的:
public boolean isPerfectSquare(int num) {
long l = 0, r = num;
while (l < r) {
long mid = l + r + 1 >> 1;
if (mid * mid <= num) l = mid;
else r = mid - 1;
}
return r * r == num;
}
果然,二分查找yyds;
去题解里看看大佬们的解法:
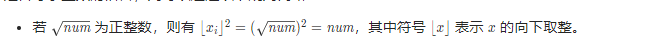
思路:使用内置的库函数
根据完全平方数的性质,我们只需要直接判断num 的平方根 x 是否为整数即可。对于不能判断浮点数的值是否等于整数的语言,则可以通过以下规则判断:
public boolean isPerfectSquare(int num) {
int x = (int) Math.sqrt(num);
return x * x == num;
}
emmm 虽然他说进阶要求是不让使用sqrt,那就再看看还有没有别的,
果然,官方题解就是不缺高大上:牛顿迭代法(我滴个乖乖,从小到大,看见牛顿总没好事)
这是牛大大的原理:(看到这个我又想起了被高数折磨的日子)
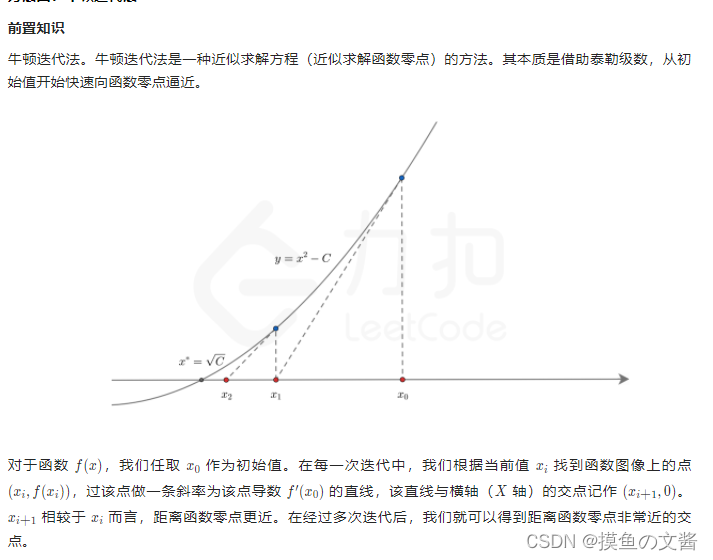

嘶~~,怎么说呢,第一次看完这个思路,我感觉他在说废话,这不就是正着说完反着说???
然后动手就没然后了,反正按我的理解实现的怎么也过不了
最后选择直接看代码,然后放弃这个解法(狗头保命).
public boolean isPerfectSquare(int num) {
double x0 = num;
while (true) {
double x1 = (x0 + num / x0) / 2;
if (x0 - x1 < 1e-6) {
break;
}
x0 = x1;
}
int x = (int) x0;
return x * x == num;
}
下面是宫水三叶大佬提供的数学思路,看这个我感觉我好像又行了,这理解清新脱俗,让人一看就懂

public boolean isPerfectSquare(int num) {
int x = 1;
while (num > 0) {
num -= x;
x += 2;
}
return num == 0;
}
今日感悟
用位运算解题,很多时候都有意想不到的效果,理解它的原理时感觉也并没有那么难,但是自己很难找到其规律和特点
还是要多多练习,多练一些题型,应该就可以找到位运算解题的条件和规律