【算法模板】DFS秒杀模板—附练习题
📒博客首页:铁甲小宝同学 📒
🌞文章目的:
DFS解题模板分享🌞🙏博主也在学习阶段,如若发现问题,请告知,非常感谢🙏
💗
同时也非常感谢各位小伙伴们的支持💗🌈每日一语:心之所愿,无所不能! 🌈
?
オレはいつかこの一味にも负けない仲间を集めて、世界一の财宝を见つけて、绝対なってやる!海贼王に!?
总有一天,我会聚集一群不输给这些人的伙伴,并找到世界第一的财宝,我要当海贼王!!!

相关算法模板推荐:
| 名称 |
|---|
| 【算法模板】BFS秒杀模板 |
| 敬请期待 |
DFS算法简介
DFS其实叫深度优先搜索算法,起始它只是一种搜索的方法思路,并没有固定的算法格式。我们通常形容他是一条路走到黑。
事实上,深度优先搜索属于图算法的一种,英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
举例说明之:下图是一个无向图,如果我们从A点发起深度优先搜索(以下的访问次序并不是唯一的,第二个点既可以是B也可以是C,D),则我们可能得到如下的一个访问过程:A->B->E(没有路了!回溯到A)->C->F->H->G->D(没有路,最终回溯到A,A也没有未访问的相邻节点,本次搜索结束).简要说明深度优先搜索的特点:每次深度优先搜索的结果必然是图的一个连通分量.深度优先搜索可以从多点发起.如果将每个节点在深度优先搜索过程中的"结束时间"排序(具体做法是创建一个list,然后在每个节点的相邻节点都已被访问的情况下,将该节点加入list结尾,然后逆转整个链表),则我们可以得到所谓的"拓扑排序",即topological sort。
DFS复杂度的分析
DFS算法是一一个递归算法,需要借助一个递归工作栈,故它的空问复杂度为O(V)。
遍历图的过程实质上是对每个顶点查找其邻接点的过程,其耗费的时间取决于所采用结构。
邻接表表示时,查找所有顶点的邻接点所需时间为O(E),访问顶点的邻接点所花时间为O(V),此时,总的时间复杂度为O(V+E)。
邻接矩阵表示时,查找每个顶点的邻接点所需时间为O(V),要查找整个矩阵,故总的时间度为O(V^2)。
v为图的顶点数,E为边数。
DFS算法的基本思路
深度优先遍历图的方法是,从图中某顶点v出发:
DFS代码模板(Java版和Python版)
前言:
因为博主也是双语言使用者,但是由于对Java基础的不扎实之前的模板和题解就没有写Java版的。但是我觉得还是要挑战一下自己,因为这样不仅可以帮助的学习Java的小伙伴们,而且还能提升博主自己的Java基础水准(在用Java写算法的时候是真的痛苦5555)。看在博主这么用心的份上大伙来个一键三联吧!!!好了,话不多说直接开始上模板!

排列类型模板
众所周知,在LeetCode上我们经常能看见一些排列的问题,我们就拿全排列来举例吧。
题目:全排列
给定一个不含重复数字的数组
nums,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:输入:nums = [1]
输出:[[1]]
从题目中我们能大概的了解题意—就是把一个nums数组中的所有的数拿来进行一个打乱顺序的排序。这种类型的题就是输入DFS中的回溯剪枝问题。而且本题还是面试中的高频题!!!
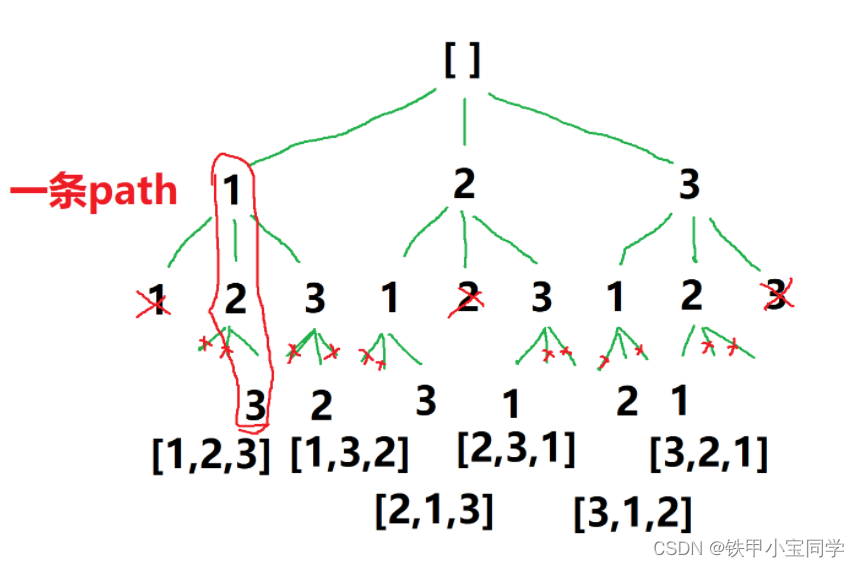
**思路:**本题就是通过一个递归然后一直给path路径数组添加新的元素。最后如果path数组的长度是等于nums数组的长度,则则需要把path数组添加到我们最终需要返回的数组res里面。而本题的核心就在于剪枝和递归的终止条件问题上面。剪枝是需要在递归时不会让path数组反复把同一个元素添加到里面,而是添加nums数组中不同的元素。而递归的终止条件在上面我们也说过,就是如果路径数组path的长度达到了和nums数组相同的长度时,我们就需要终止其继续递归并把路径数组path添加到结果数组res里面。
欧克,大体的思路就是这样。为了更深入的了解本题,我们可以继续向下看看本题的解决代码。
Java版本:
class Solution {
//创建返回的数组res和路径数组path
List<List<Integer>> res = new ArrayList<List<Integer>>();
List<Integer> path = new ArrayList<Integer>();
public List<List<Integer>> permute(int[] nums) {
//获取nums数组的长度,作为下面的终止条件。
int n = nums.length;
//进行一个dfs
dfs(n,nums);
return res;
}
//创建一个dfs方法,用来查找不同种的排列顺序。
public void dfs(int n,int[] nums){
//设置终止条件
if(path.size() == n){
//如果达到终止条件就证明path已经得到了一种排序,并把这个添加到res数组里面。
res.add(new ArrayList<Integer>(path));
//终止继续递归!
return ;
}
//设置for循环来对nums数组得遍历和让path数组对其进行添加新的不同元素
for (int i = 0 ; i < n ; i ++){
//设置一个判断,path路径中已经包含了这个元素,则需要跳过此次循环,如果没有则继续向下递归。
if (path.contains(nums[i])){
continue;
}
//为path数组提添加新的元素。
path.add(nums[i]);
//继续递归
dfs(n , nums);
//先删除最后一个元素,重新继续组合新的排序。
path.remove(path.size() - 1);
}
}
}
Python版本:
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
#创建一个返回列表res
res = []
#定义一个dfs函数
def dfs(path,nums):
#设置判断条件,如果路径列表长度等于nums列表长度则终止递归且把path列表添加到res列表当中。
if len(nums) == len(path):
res.append(path[:])
return
#进行一个for循环,对路径列表逐一进行添加。
for i in nums:
#判断如果nums中某个元素已经在路径列表path当中,则为了避免path列表出现重复的元素。
if i in path:
continue
#继续递归,且在path列表当中添加新的元素
dfs(path + [i] , nums)
#执行dfs函数
dfs([],nums)
#返回最后的res列表
return res

**本题小结:**通过上面的思路和代码,我们能也能总结出来
dfs方法的一些特点:
- dfs需要一直递归到一个终止条件。
- 在使用路径数组path时我们可以发现,其实path数组就是一个栈的形式,每次都会有
入栈和出栈。- 递归当中其实就好比一个
树,需要不断的剪枝和终止条件。其实dfs掌握上面的核心特点,在做题的时候我们就能知道大概的思路。因为有些题就是在这个上面稍微做了一个简单的修改,我们只需要
掌握核心科技,妈妈就不用担心我不会做dfs类型的题啦。
在做过了全排列这个简单的DFS习题后我们接着再来一个简单的DFS习题吧!
题目: 子集 II
给你一个整数数组
nums,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:输入:nums = [0]
输出:[[],[0]]
从题目我们大概的能知道:
- nums包含重复元素。
- 解集中不能包含重复的解。
OK,我们做题知道了大题的思路后我们就更容易的下手来完成这个题目了。
思路:
首先我们知道这个nums里面包含有重复的元素,但是题目没有给我们说是不是有序的。所有这个我们首先需要对这个
nums数组进行一个排序。我们还知道解集中不让出现重复的解,也就是说如果在nums数组里面有相同的元素一般会有两个相同的解。所有为了去除这个重复的解我们就需要在循环时跳过相同的元素,避免出现相同的结果。
大体思路我们已经分析了,接下来就是对代码的逐一分析。
Java版本:
class Solution {
//创建返回结果数组res和路径数组path
List<List<Integer>> res = new ArrayList<List<Integer>>();
List<Integer> path = new ArrayList<Integer>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
//对数组nums先进行一个排序(因为这样更容易跳过相同的元素)
Arrays.sort(nums);
//执行dfs方法。
dfs(nums,0);
return res;
}
//创建一个dfs方法。
void dfs(int[] nums,int idx){
//因为需要不同的子集,长度已经不再是添加的必要条件;
res.add(new ArrayList<Integer>(path));
//长度是一个终止条件!
if (path.size() == nums.length){
return ;
}
//每层递归需要缩减一个循环范围,避免重复。
for (int i = idx ; i < nums.length ; i ++){
//用来判断相同元素,如果相同则跳过
if (i > idx && nums[i-1] == nums[i]) continue;
//入栈
path.add(nums[i]);
//继续递归
dfs(nums,i + 1);
//出栈
path.remove(path.size() - 1);
}
}
}
Python版本:
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
#创建dfs函数。
def dfs(begin,path):
#对nums数组进行循环
for i in range(begin,len(nums)):
#如果如见相同元素则跳过。
if i>begin and nums[i-1] == nums[i]:
continue
#入栈
path.append(nums[i])
#把path路径数组添加到res返回数组里面。
res.append(path[:])
#继续递归添加
dfs(i+1,path)
#出栈
path.pop()
#设置返回数组
res = []
#对nums数组进行一个排序,以便检查出重复的元素。
nums.sort()
#对给的nums数组判断里面是否存在元素,如果没有存在元素就直接返回一个空集。
if len(nums) == 0:
return [[]]
#添加一个空集
res.append([])
#进行一个dfs让res获取里面的数。
dfs(0,[])
#返回数组res,即就是我们所获取的全集。
return res
欧克,上面两题就是一个大概的DFS模板。大家只需要记住DFS核心就是需要递归和一个栈。
接下来还是老规矩——给大家加餐哦!!
| 题目 |
|---|
| 47. 全排列 II |
| 78. 子集 |
| #剑指 Offer 38 字符串的排列 |
| #39 组合总和 |
| #40 组合总和 II |
老规矩,博主可是使用模板都给拿捏了哦。大家也要加油哦!!!

树类型模板
我们在写一些树的算法题的时候其实最常用的就是DFS。因为我们需要使用一直递归直到找到树的叶子节点,才能直到这棵树的深度且有办法继续去写。那么说到这里我们就来一道求深度的算法题吧!
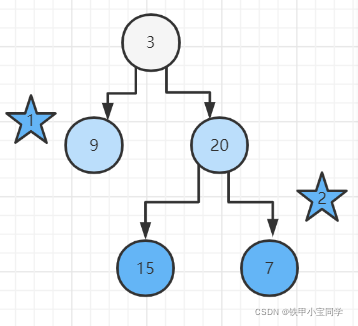
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
例如:
给定二叉树 [3,9,20,null,null,15,7],
? 3
/
9 20
/
15 7
返回它的最大深度 3 。
从本题我们能大概的直到本题的目的就是求一颗二叉树的最大深度。
思路:求最大深度,我们可以使用递归,找到左右子树到叶子节点的深度并且取最大值。
我们可以看上图左子树的最大深度是
1,而右子树的最大深度是2。则我们取深度的最大值并加上1(根节点本身也算1个深度)就是我们所需要得到的结果了。(图做的有点抽象,大家别建议5555)。
Java版本:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
//判断一个根节点是是否为空,如果为空则返回0。
if(root == null){
return 0;
}
//进行一个递归判断左子树和右子树的最大值并加上一。
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
}
Python版本:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
#思路是和Java版本的一样的。
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root:
return 0
return max(self.maxDepth(root.left),self.maxDepth(root.right)) + 1
因为树的很多大部分都是递归写法,和这个相差不太大,所以我就只给上面一个例题。接下来就是给大家附练习题了。
| 题目 |
|---|
| 剑指 Offer 28. 对称的二叉树 |
| 100. 相同的树 |
| 310. 最小高度树 |
| 145. 二叉树的后序遍历 |
| 589. N 叉树的前序遍历 |
| 590. N 叉树的后序遍历 |

表格遍历模板
本模板和BFS其实有一些地方是相同的:最常见的就是上下左右四个方向的判断。
那我们还是拿最经典的岛屿问题来讲解这个问题。
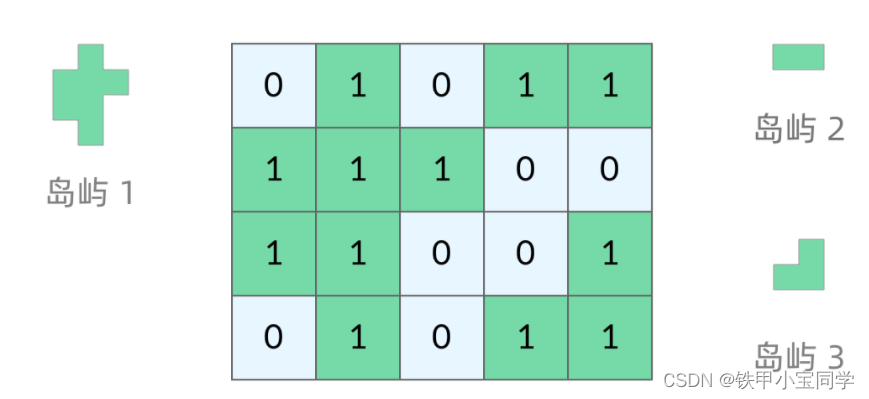
题目:200. 岛屿数量
题目:
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
示例 2:输入:grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出:3
其实本题使用DFS也是使用沉岛的思想,使用循环逐一遍历这个grid如果为1就res结果集就加一,且使用DFS沉岛。
具体的流程我们可以看代码来逐步分析。
Java版本:
class Solution {
//设置返回结果集
int res = 0;
public int numIslands(char[][] grid) {
//获取grid的长和宽。
int m = grid.length;
int n = grid[0].length;
//for循环遍历整个grid表格。
for (int i = 0 ; i < m ; i++ ){
for (int j = 0 ; j < n ;j ++ ){
//发现陆地‘1’的时候res加一,且是用dfs沉岛。
if (grid[i][j] == '1'){
res += 1;
dfs(i,j,m,n,grid);
}
}
}
//返回最后结果
return res;
}
//定义dfs方法,用来沉岛
void dfs(int x , int y,int m , int n , char[][] grid) {
//判断如果越界和不是陆地则结束递归。
if (x < 0 || y < 0 || x >= m || y >= n || grid[x][y]== '0') return ;
//如果grid[x][y] == '1',则把它变为'0'且继续使用DFS遍历x,y四周的岛屿。
grid[x][y] = '0';
dfs(x - 1,y,m,n,grid);
dfs(x + 1,y,m,n,grid);
dfs(x , y + 1,m,n,grid);
dfs(x , y - 1,m,n,grid);
}
}
Python版本:
class Solution:
#Python的大体思路是和上面Java的一样,这里我就不再过多的叙述了。
def numIslands(self, grid: List[List[str]]) -> int:
x = len(grid)
y = len(grid[0])
def dfs (grid,i,j):
if i < 0 or j < 0 or i >= x or j >= y or grid[i][j] =='0':
return
grid[i][j] = '0'
dfs (grid,i-1,j)
dfs (grid,i+1,j)
dfs (grid,i,j-1)
dfs (grid,i,j+1)
num = 0
for i in range(x):
for j in range(y):
if grid[i][j] == '1':
dfs(grid,i,j)
num += 1
return num
因为岛屿这种表格题也是非常简单的,无论是使用DFS还是BFS。我们都可以套用模板来解决这种类型的问题,但是为了能更好的提高自己的算法能能力,博主还是建议大家能够去多多练习的,同时下面也整理了一些习题为大家加餐。
| 题目 |
|---|
| 463. 岛屿的周长 |
| 695. 岛屿的最大面积 |
| 827. 最大人工岛 |
| 1905. 统计子岛屿(中等) |
| 694. 不同的岛屿数量(中等) |
| 1020. 飞地的数量(中等) |

总结
本文也是到了尾声,同时非常感谢能看到这里的小伙伴们,也更希望本文能对你们有所帮助。这个系列—算法模板如果没有什么意外博主是会一直更新下去的,更希望能帮助一下初学的小伙伴们。
每一篇文章都是博主十分用心创作出来的,如果能给大家带来帮助希望大家来个一键三连。这将会是博主最大的动力哦!!!
OK,今天的文章分享就到这里,我们下期见!!!