希尔排序
希尔排序(Shell Sort)是插入排序的一种,它是针对直接插入排序算法的改进。
希尔排序又称缩小增量排序,因 DL.Shell 于 1959 年提出而得名。
它通过比较相距一定间隔的元素来进行,各趟比较所用的距离随着算法的进行而减小,直到只比较相邻元素的最后一趟排序为止。
二、适用说明
希尔排序时间复杂度是?O(n^(1.3-2)),空间复杂度为常数阶?O(1)。希尔排序没有时间复杂度为?O(n(logn))?的快速排序算法快 ,因此对中等大小规模表现良好,但对规模非常大的数据排序不是最优选择,总之比一般?O(n^2 )?复杂度的算法快得多。
三、过程图示
希尔排序目的为了加快速度改进了插入排序,交换不相邻的元素对数组的局部进行排序,并最终用插入排序将局部有序的数组排序。
在此我们选择增量?gap=length/2,缩小增量以?gap = gap/2?的方式,用序列?{n/2,(n/2)/2...1}?来表示。
如图示例:
(1)初始增量第一趟?gap = length/2 = 4
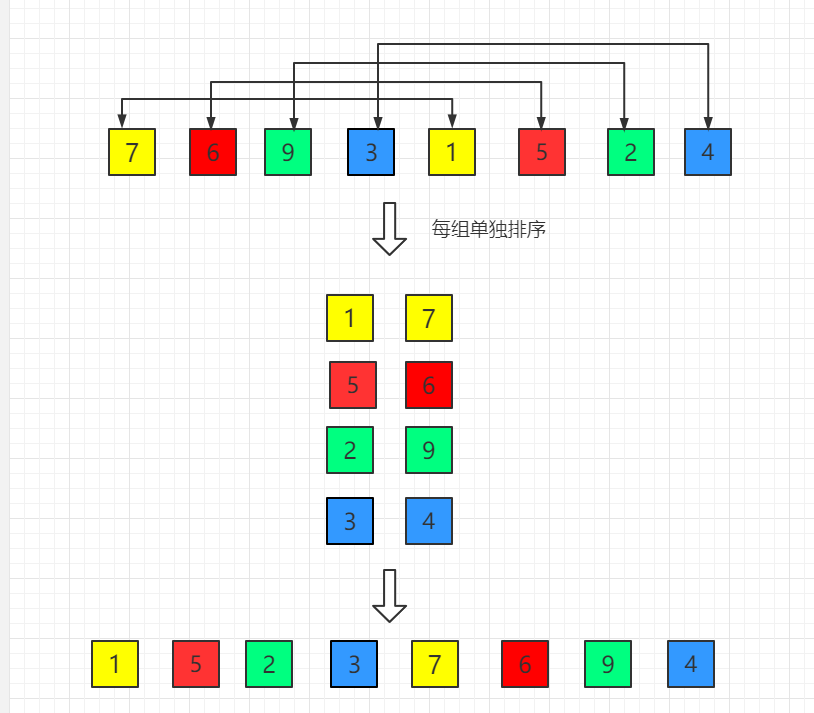
(2)第二趟,增量缩小为 2
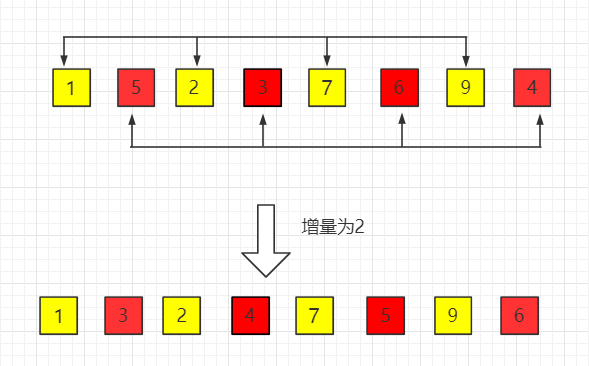
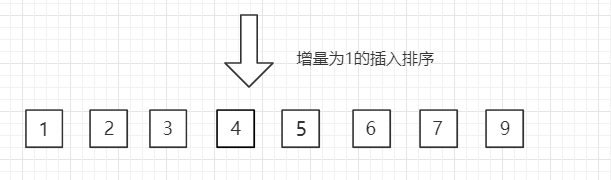
(3)第三趟,增量缩小为 1,得到最终排序结果
四、Java 实例代码
//希尔排序
public void shellSort(int[]arr){
int gap=arr.length>>1;
while (gap>1){
insertionSortByGap(arr,gap);
gap/=2;
}
insertSort(arr);
}
private void insertionSortByGap(int[] arr, int gap) {
for (int i=gap;i< arr.length;i++){
for (int j=i; j-gap>=0&&arr[j]<arr[j-gap];j-=gap){
swap(arr,j-gap,j);
}
}
}
//归并排序归并排序
?一、概念及其介绍
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
二,过程图解
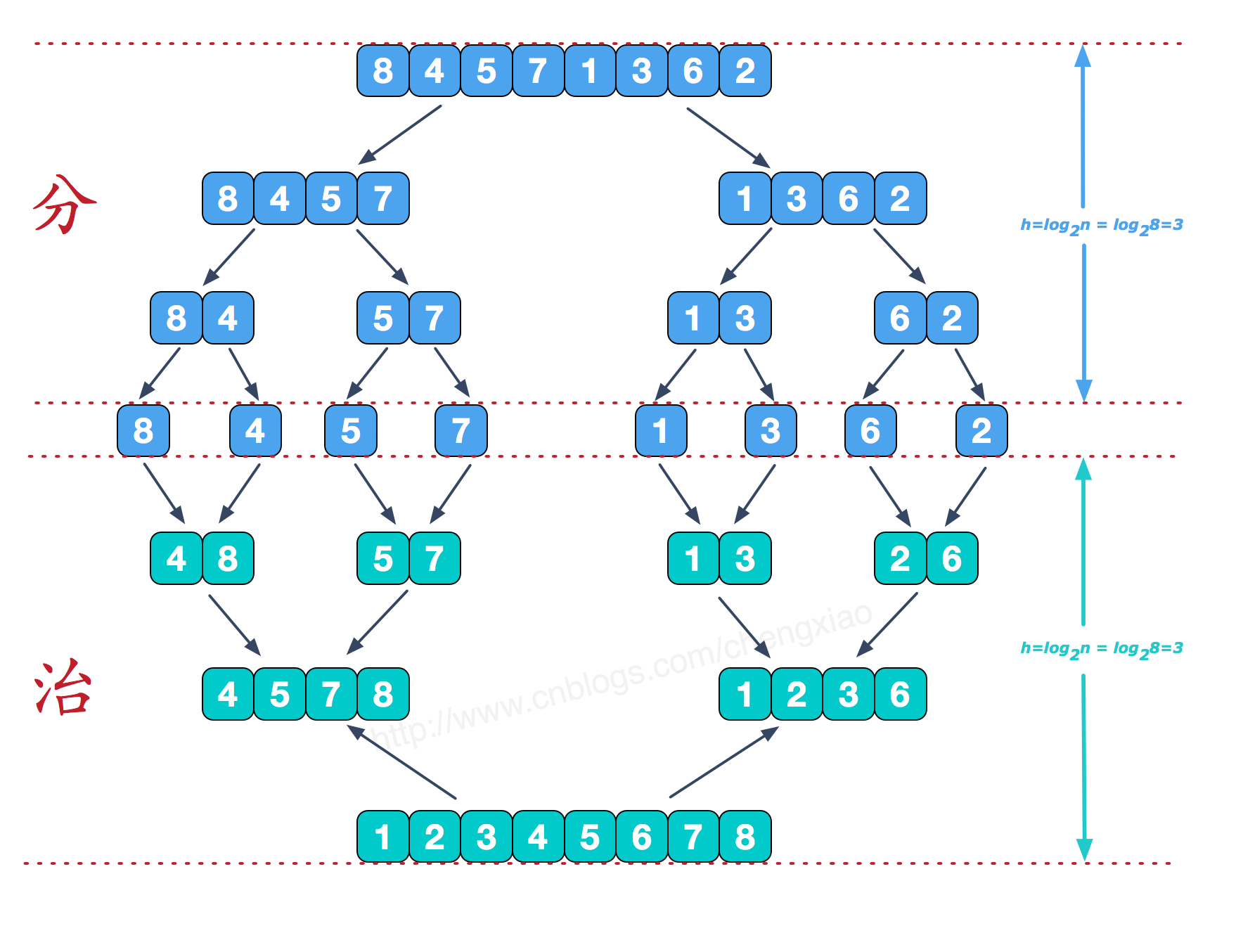
? 可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。
三, java代码实现
//归并排序
public void mergeSort(int []arr){
mergeSortInternal(arr,0,arr.length);
}
private void mergeSortInternal(int []arr,int l,int r) {
//小区间直接使用插入排序
if(r-l<=15){
insertionSort(arr,l,r);
return;
}
int mid=l+(r-l)>>1;
mergeSortInternal(arr,l,mid);
mergeSortInternal(arr,mid+1,r);
if (arr[mid]>arr[mid+1]){
merge(arr,l,mid,r);
}
}
private void insertionSort(int[] arr,int l,int r) {
for (int i=l+1;i<r;i++){
for (int j=i;j>l&&arr[j]<arr[j-1];j--){
swap(arr,j,j-1);
}
}
}
private void merge(int[] arr, int l, int mid, int r) {
//先创立一个新的数组anx
int[] aux = new int[r - l + 1];
//将arr上的元素拷贝到aux上
for (int i=0;i<aux.length;i++){
aux[i]=arr[i+l];
}
int i=l;
int j=mid+1;
for (int k=l;k<=r;k++){
if (i>mid){
arr[k]=aux[j-l];
j++;
}
if (j>l){
arr[k]=aux[i-l];
i++;
}
else if (aux[i-l]<=aux[j-l]){
arr[k]=aux[i-l];
i++;
}
else {
arr[k]=aux[j-l];
j++;
}
}
}
?