[数据结构与算法]简单算法——二分搜索的递归版本和非递归版本

二分搜索

这是大家比较熟悉的算法了，我们今天来复习一下：

前提：二分查找要求所查找的顺序表必须是有序的。

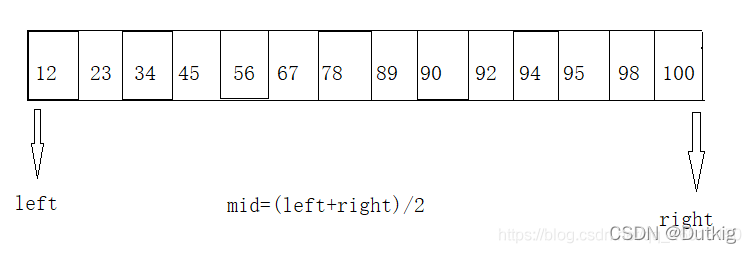
算法思路

定义left为顺序表最左端元素位置，right为顺序表右端元素位置。定义mid = (left + right) / 2,即顺序表的中间位置，然后用所查找的值与mid所在位置处的值比较，由于列表有序，若所查找的值比mid小，则只需在表的前半部分查找，否则只需在表的后半部分查找（若第一次比较就发现两值相等则直接返回当前值所在的位置），以此类推，直至查找到所寻找的值或确定所查找的值不在该列表内为止（即查找失败）。

普通二分搜索

int Binary_search(vector<int>& num, int tag) // 二分查找
{
	int n = num.size();
	if (n == 0)
	{
		return -1;
	}
	int left = 0;
	int right = n - 1;
	int pos = -1;
	while (left <= right)//注意这里的等号，最后如果走到一起还要比较一次
	{
		int mid = (right + left) / 2;
		if (tag < num[mid])
		{
				right = mid - 1;
		}
		else if (tag > num[mid])
		{
			left = mid + 1;
		}
		else
		{
			if (mid > left && num[mid - 1] == tag)  //多个重复数字返回第一个数字下标
			{
				right = mid - 1;
			}
		
			if (mid < right && num[mid + 1] == tag)  //多个重复数字返回最后一个数字下标
			{
				left = mid + 1;
			}
			
			else
			{
				pos = mid;
				break;
			}
		}
	}
	return pos;
}

int main()
{
	vector<int> ar = { 12,12,12,12,23,23,24,24,25,25 };
	cout << Binary_search(ar, 12) << endl;
}

二分搜索算法，实际上就是对BST树（二叉搜索平衡树）（搜索树：每一个结点的值都大于左子树的结点的值，都小于右子树结点的值）从root根结点开始搜索的过程，每一次搜索只会沿着一条路径搜索下去，不可能同一次搜索多条路径。

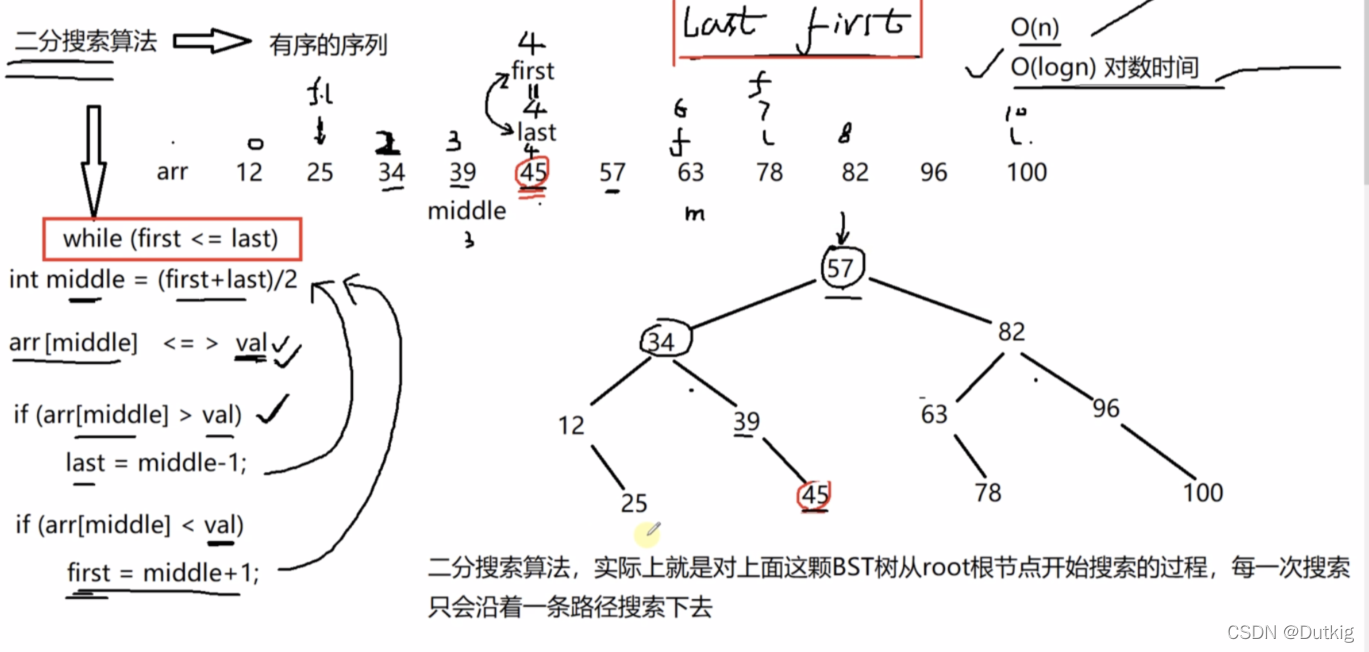
二分搜索的算法的时间复杂度就是上面这棵BST树的层数/高度：
计算方式：问题规模n = 结点个数 ==> 解除出来的层数就是时间复杂度（因为每一次搜索每一层沿着一条路径）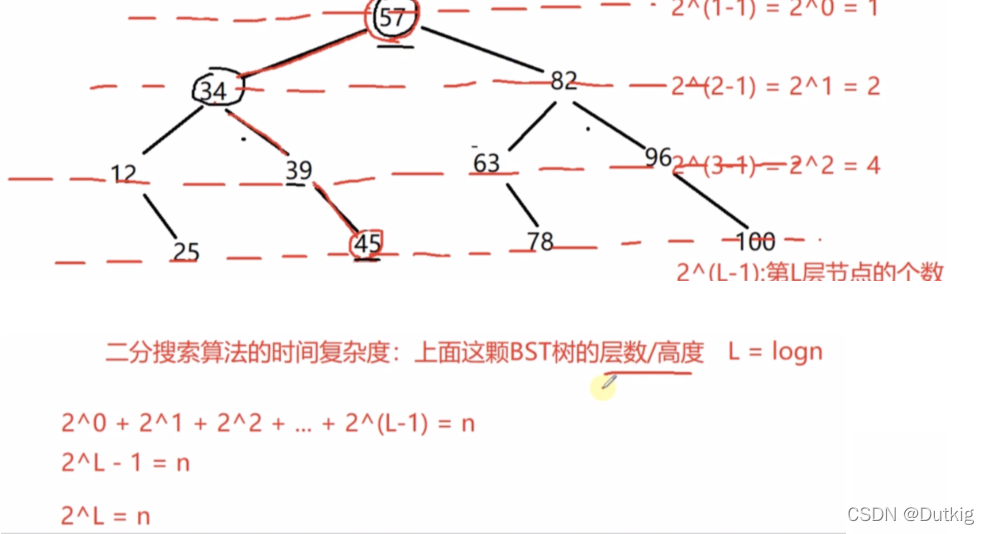

递归二分搜索

int Recursion_Binary_search(vector<int>&ar, int left, int right, int key)
{
	if (left > right)//查找不到
		return -1;
	int pos = -1;
	int mid = (left + right) / 2;
	while (left <= right)
	{
		if (key < ar[mid])
			return Recursion_Binary_search(ar, left, mid - 1, key);
		else if (key > ar[mid])
			return Recursion_Binary_search(ar, mid + 1, right, key);
		else //查找到
		{
			if (mid > left && ar[mid - 1] == key)  //多个重复数字返回第一个数字下标
			{
				Recursion_Binary_search(ar, left, mid - 1, key);
			}
			else
			{
				pos = mid;
				break;
			}
		}
	}
	return pos;
}

int main()
{
	vector<int> ar = { 12,12,12,12,23,23,24,24,25,25 };
	cout << Recursion_Binary_search(ar, 0, ar.size() - 1, 25) << endl;
}