[数据结构与算法]循环赛日程安排问题--分治

问题描述：
设有n=2k（k为上标）个选手要进行网球循环赛，要求设计一个满足以下要求的比赛日程表：
（1）每个选手必须与其他n-1个选手各赛一次；
（2）每个选手一天只能赛一次。
按此要求，可将比赛日程表设计成一个 n 行n-1列的二维表，其中，第 i 行第 j 列表示和第 i 个选手在第 j 天比赛的选手。
分治策略：
按照分治的策略，可将所有参赛的选手分为两部分，n＝2k（k为上标）个选手的比赛日程表就可以通过为n/2＝2k-1（k-1为上标）个选手设计的比赛日程表来决定。递归地执行这种分割，直到只剩下2个选手时，比赛日程表的制定就变得很简单：只要让这2个选手进行比赛就可以了。

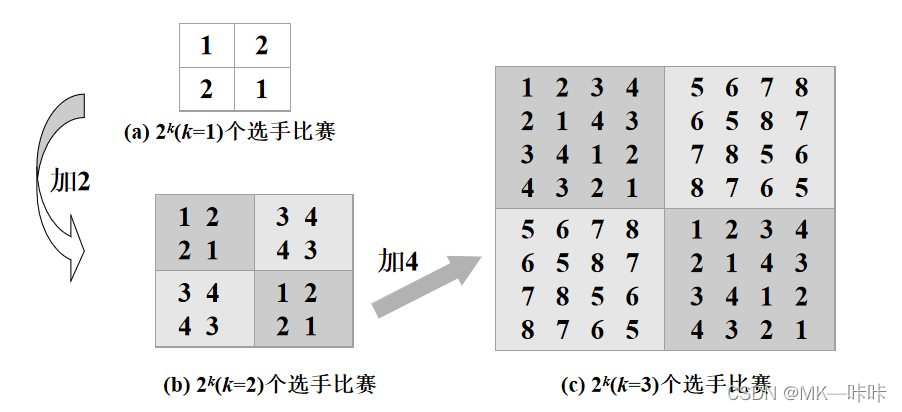
显然，这个求解过程是自底向上的迭代过程，其中左上角和左下角分别为选手1至选手4以及选手5至选手8前3天的比赛日程，据此，将左上角部分的所有数字按其对应位置抄到右下角，将左下角的所有数字按其对应位置抄到右上角，这样，就分别安排好了选手1至选手4以及选手5至选手8在后4天的比赛日程，如图?所示。具有多个选手的情况可以依此类推。

void GameTable(int k, int a[ ][ ])
     {  
        // n=2k(k≥1)个选手参加比赛，
        //二维数组a表示日程安排，数组下标从1开始
         n=2;       //k=0，2个选手比赛日程可直接求得
         //求解2个选手比赛日程，得到左上角元素
         a[1][1]=1; a[1][2]=2;   
         a[2][1]=2; a[2][2]=1;
         for (t=1; t<k; t++)
         //迭代处理，依次处理22, …, 2k个选手比赛日程
         {
                temp=n; n=n*2;   
        //填左下角元素
        for (i=temp+1; i<=n; i++ )
            for (j=1; j<=temp; j++)
                a[i][j]=a[i-temp][j]+temp;
                //左下角元素和左上角元素的对应关系
       //填右上角元素
       for (i=1; i<=temp; i++)       
           for (j=temp+1; j<=n; j++)
              a[i][j]=a[i+temp][(j+temp)% n];
       //填右下角元素
      for (i=temp+1; i<=n; i++)
          for (j=temp+1; j<=n; j++)
             a[i][j]=a[i-temp][j-temp];
    }
}
 

分析算法的时间性能，迭代处理的循环体内部有3个循环语句，每个循环语句都是一个嵌套的for循环，且他们的执行次数相同，基本语句是最内层循环体的赋值语句，即填写比赛日程表中的元素。基本语句的执行次数是：

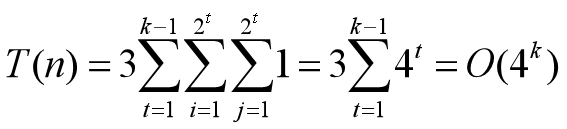
所以，算法时间复杂性为O(4k)。