递归算法(英语:recursion algorithm)在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。递归式方法可以被用于解决很多的计算机科学问题,因此它是计算机科学中十分重要的一个概念。绝大多数编程语言支持函数的自调用,在这些语言中函数可以通过调用自身来进行递归。计算理论可以证明递归的作用可以完全取代循环,因此在很多函数编程语言(如Scheme)中习惯用递归来实现循环。
?递归形式的应用范围是非常广泛的,我们常说的深度优先搜索DFS算法就是用递归形式实现的,本文仅介绍涉及枚举的递归,它们也可以归类到DFS算法。
枚举算法是我们在日常中使用到较多的一种算法,它的核心思想就是:枚举所有的可能。枚举法的本质就是从所有候选答案中去搜索正确的解,使用该算法需要满足两个条件:(1)可预先确定候选答案的数量;(2)候选答案的范围在求解之前必须有一个确定的集合。
最简单的枚举问题:答案是单一信息(比如答案是一个数字),此时只需使用循环即可枚举所有答案,例如找到小于N的最大质数,找到数组中的最大值......
也有一些问题,答案是一个序列或排列,此时就无法用循环来解决问题。可以用递归的方式找到子序列、组合、或者排列,然后对答案进行筛选。比如经典的“N皇后问题”,其答案是一个N的全排列,而背包问题(选择不超过背包容量的最大价值物品),其最终答案是一个子序列。需要注意的是,递归枚举的时间复杂度极高,因此只适用于n比较小的情况,或者是实在想不出来正确解法时用来获得基础分数(骗分)。
本文介绍子序列、组合、全排列的递归写法。
基础递归思想如下(以组合为例):F(n个数字,取m个),根据第一个数字选中还是不选中,可以分解为F(n-1个数字,取m-1个)+ F(n-1个数字,取m个)。在代码实现过程中,需要设计(1)设定参数确定选取范围和已选取个数,(2)如何存储答案和避免重复选取。在遇到具体问题时,还要考虑在算法中加入限定语句减少递归次数(剪枝)或做进一步的优化。
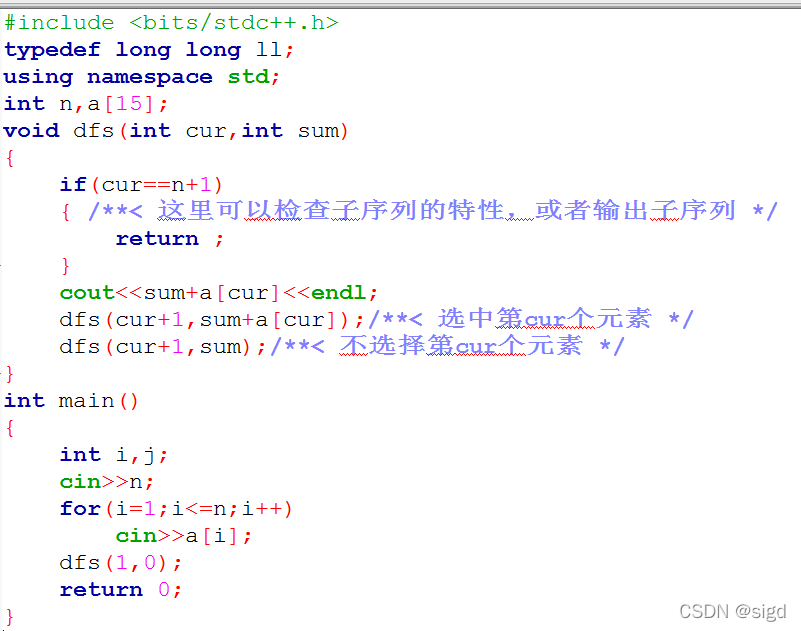
(一)递归实现指数型枚举(子序列)

?
(二)递归实现组合枚举(组合)
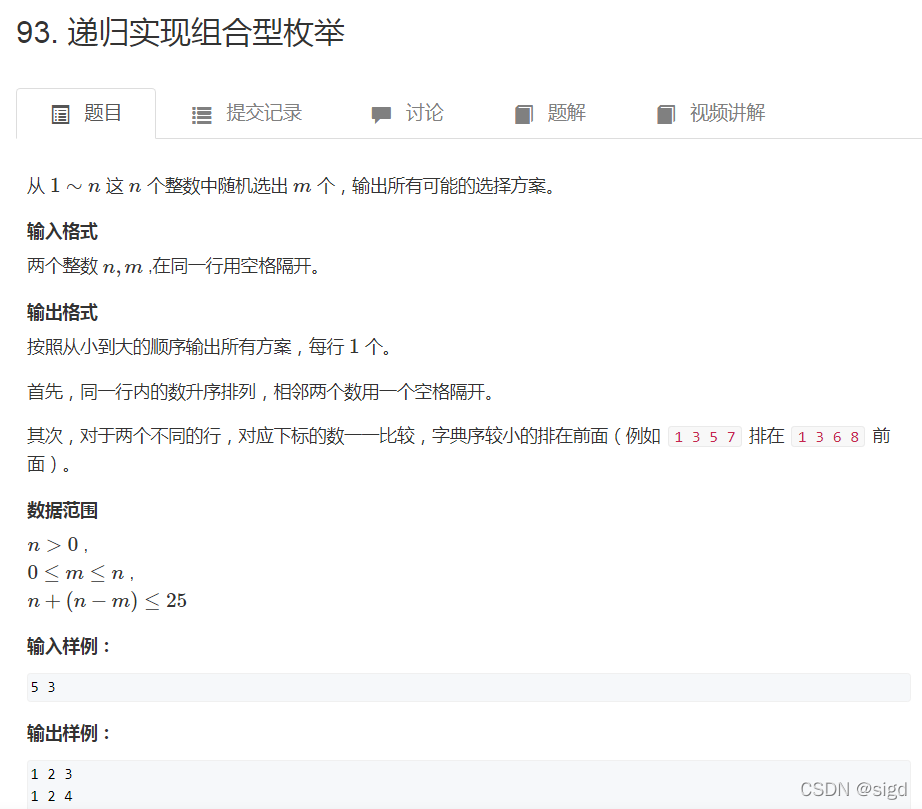
?
(三)递归实现排列枚举(排列)
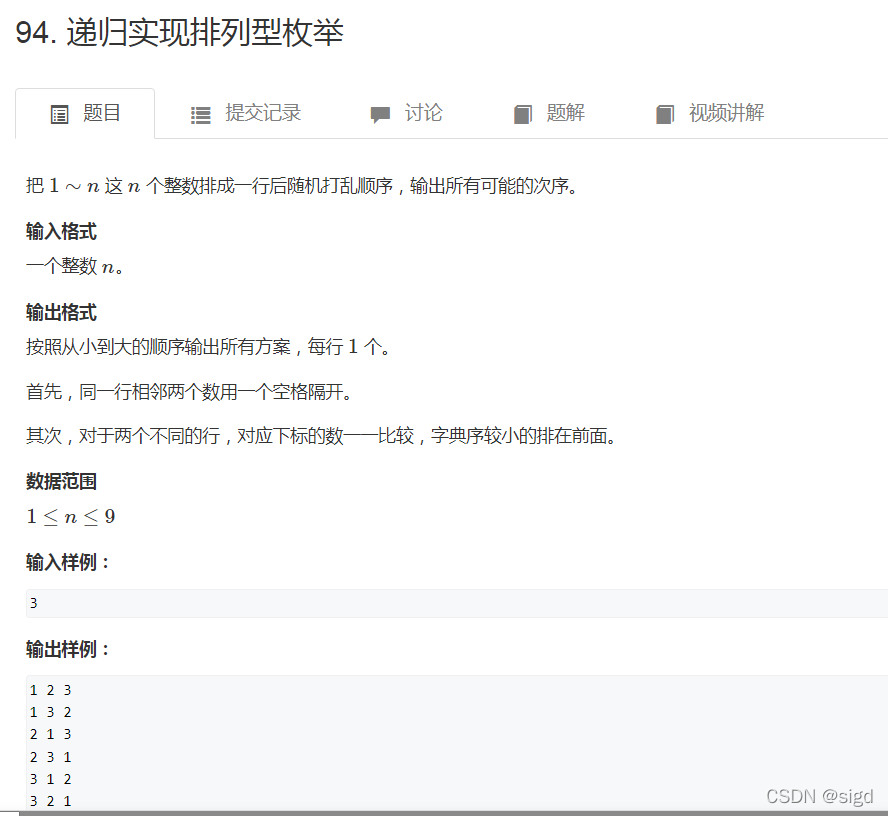
 ?
?
?