根据数组创建二叉树【DS + C++】
前言
刷了很多树的题目了,突然想在本地ide上运行一些测试用例,这时候需要我们在代码中新增树的创建的部分。语言为C++,ide为 visual studio 2022。
知识点——二叉树
二叉树是树的一种,而树相较于图,算是一种较为直观的数据结构,一棵完整的树包括根节点,中间节点,以及叶子节点。根节点是树的开始节点,有子节点,没有父节点,叶子节点是指树的最底层,子节点指向空,其实就是没有子节点,有父节点,而中间节点则是既有子节点也有父节点。当然这些节点的定义和解释基于一个前提:该树的节点树 > 1。而对于一棵树,题目往往会给出根节点 root,因为树的任一个节点都只能通过自身去访问子节点,而不能访问父节点,所以为了能够访问整颗树,往往会给出根节点。欸?单向访问,听起来和我们之前学过的单链表是不是很类似呢?只不过单链表的节点只有next后向指针,指针指向下一个节点,而树的子节点指针却是可以有多个。
树的结构图
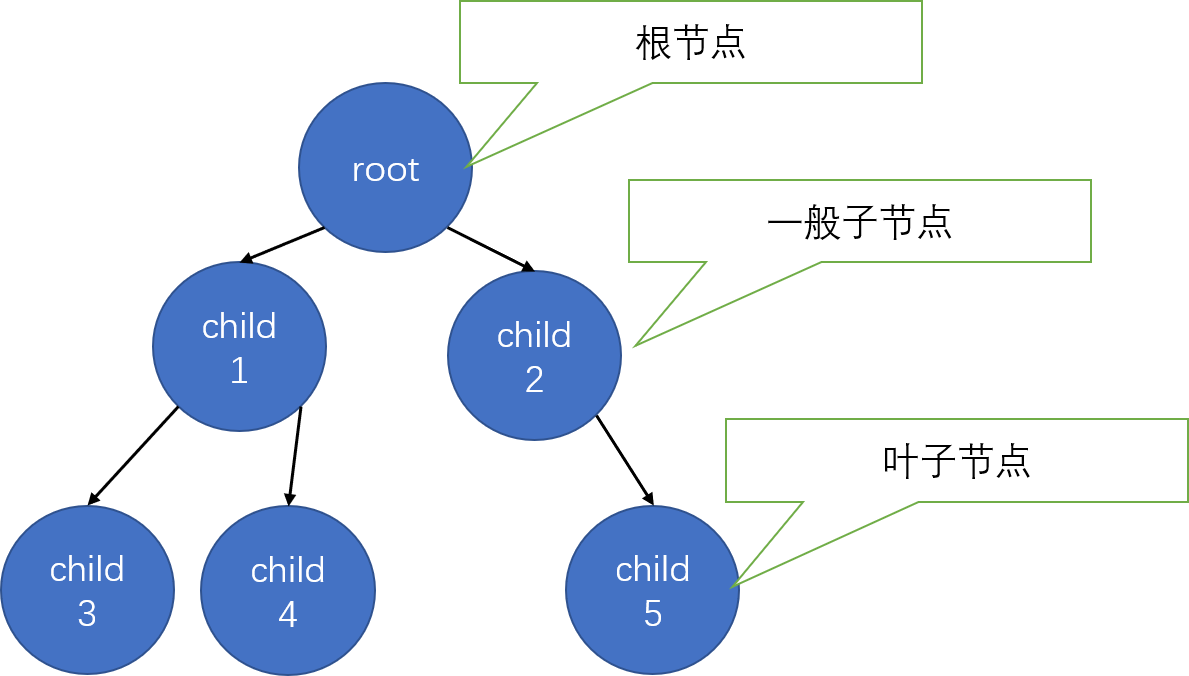
那么二叉树其实就很好理解了,二叉树其实就是每个节点都有两个子节点,分别为 left 和 next,两个指针,指向子节点。当然叶子节点的left和right自然指向空。
我之前写过一篇题解,当然那一篇并不是二叉树,而是n叉树,其实n叉树就是二叉树的 plus 版本,每个节点有n个子节点,相信聪明的你看到这里一定知道n个节点指针是以数组的形式存储了吧。
附上传送门链接 leetcode 559 每日一题题解 N叉树的最大深度——DFS与BFS_物联黄同学的博客-CSDN博客
根据数组创建二叉树
像我们平时在做leetcode或者牛客的题目的时候,往往题目给的数据并不是直接给一个数据指针啥的,而是会以数组的形式给出,如下图。

这里请忽略输出和解释哈。
数组中的null表示当前位置为空,也就是val=2的left节点是空的。
我们的任务就是要对形如这样的数组的数据,构造一个二叉树。
核心代码(C++)
首先我们要先定义树的节点
// 定义二叉树节点
struct TreeNode
{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(): val(0), left(nullptr), right(nullptr) {}
TreeNode(int x): val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode *right): val(x), left(left), right(right){}
};
然后由于输入中有null字样,我们需要使用字符串数组,存储输入。
在我们构建的时候需要先对字符串判断是否是null,如果不是则利用sstream库(字符串流)的stoi()函数,将字符串转换为int整数。然后再用整数生成相应节点。
而在构建树的时候,我们观察输入的数组,其实不难发现这是一个按BFS顺序的树的节点遍历顺序。所以我们可以使用对列去存储节点,然后以 BFS 的方式构建数组。
在构建完数组之后我们还可以使用还是 BFS 的方法,将整颗树输出展示出来。
下面是完整代码,请忽略Solution部分,这是leetcode一道题目的题解代码。
Code(C++)
#include<iostream>
#include<string>
#include<vector>
#include<queue>
#include<sstream>
using namespace std;
// 定义二叉树节点
struct TreeNode
{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(): val(0), left(nullptr), right(nullptr) {}
TreeNode(int x): val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode *right): val(x), left(left), right(right){}
};
class Solution
{
public:
string tree2str(TreeNode* root)
{
if (root == nullptr)
{
return "";
}
else if (root->left == nullptr && root->right == nullptr)
{
return to_string(root->val);
}
else if (root->right == nullptr)
{
return to_string(root->val) + "(" + tree2str(root->left) + ")";
}
return to_string(root->val) + "(" + tree2str(root->left) + ")(" + tree2str(root->right) + ")";
}
};
// 构造一下二叉树
class BinaryTree
{
public:
TreeNode* root; // 根节点
/// <summary>
/// BFS——根据数组构建二叉树
/// 数组中节点的顺序表示的就是BFS的顺序
/// 所以使用BFS 完成搜索
/// </summary>au
/// <param name="nodes"></param>
BinaryTree(vector<string> nodes)
{
// 下标索引
int i = 0;
// 数组尺寸
int n = nodes.size();
// 先判断根节点是否是空
if (nodes[0] == "null" && n == 1)
{
root = nullptr;
return;
}
// 非空则新建根节点
stringstream ss;
ss << nodes[0];
int val;
ss >> val;
root = new TreeNode(val);
i++;
// 节点对列
queue<TreeNode*> que;
// 先将根结点入队
que.push(root);
// 当对列不空且未遍历完时
while (!que.empty() && i < n)
{
// 获取节点并出队
TreeNode* node = que.front();
que.pop();
// 然后给左右指针
for (int j = 1; j <= 2 && i < n; ++j, ++i)
{
// 若空则置空
if (nodes[i] == "null" && j == 1)
{
node->left == nullptr;
}
else if (nodes[i] == "null" && j == 2)
{
node->right = nullptr;
}
// 非空则生成节点并入队
else if(j == 1)
{
node->left = new TreeNode(stoi(nodes[i]));
que.push(node->left);
}
else
{
node->right = new TreeNode(stoi(nodes[i]));
que.push(node->right);
}
}
}
}
/// <summary>
/// 展示树的结构
/// 为了能够清晰展示,还是使用BFS
/// </summary>
void display()
{
// 若根节点为空
if (root == nullptr)
{
return;
}
// 非空入队
queue<TreeNode*> que;
que.push(root);
// 每一层节点的数量,包括空节点
int t = 0, num = 1;
while (!que.empty())
{
TreeNode* node = que.front();
que.pop();
cout << node->val << " ";
num--;
for (int i = 0; i < 2; ++i)
{
TreeNode* child;
if (i == 0)
{
child = node->left;
}
else
{
child = node->right;
}
if (child != nullptr)
{
que.push(child);
t++;
}
}
// 当num = 0 时,说明当层遍历完,需要换行,进入下一层
if (num == 0)
{
cout << endl;
num = t;
t = 0;
}
}
}
};
int main(int agrc, char** argv)
{
int n;
cin >> n;
vector<string> nodes(n);
for (int i = 0; i < n; ++i)
{
cin >> nodes[i];
}
BinaryTree* bt = new BinaryTree(nodes);
bt->display();
return 0;
}
后话
不要摆烂噢,不然就会变菜了 _