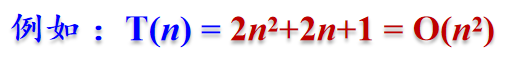一、相关概念
1、算法分析
实际上就是分析算法占用的资源。
目的:分析算法的时空效率以便改进算法性能。
包括:
- 时间性能分析:分析算法占用的CPU时间。
- 空间性能分析:分析算法占用的内存空间。
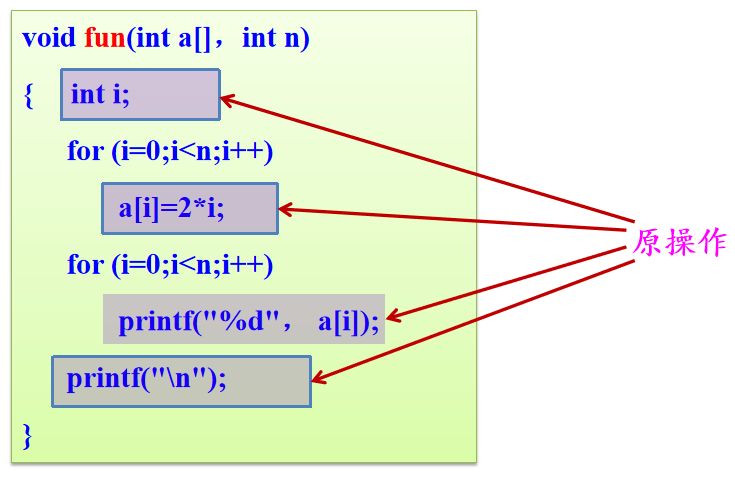
2、原操作
指固有数据类型的操作,如+、-、*、/、++和--等。
3、时间复杂度
一个算法是由控制结构(顺序、分支和循环三种)和原操作构成的。算法执行时间取决于两者的综合效果。
4、空间复杂度
用于量度一个算法在运行过程中临时占用的存储空间大小。
二、时间性能分析的方法
- 事后分析统计方法:编写算法对应程序,统计其执行时间。但由于编写语言不同、执行程序的环境不同,所以不能用算法的绝对执行时间进行比较。
- 事前估算分析方法:撇开编写语言、执行环境等因素,认为算法的执行时间是问题规模n(number)的函数。?
三、分析算法的执行时间的流程
- 求出算法所有原操作的执行次数(频度)。
- 算法执行时间大致 = 原操作所需的时间?× 执行次数。所以执行次数与算法的执行时间成正比。
- 比较不同算法的执行时间确定最优的算法。
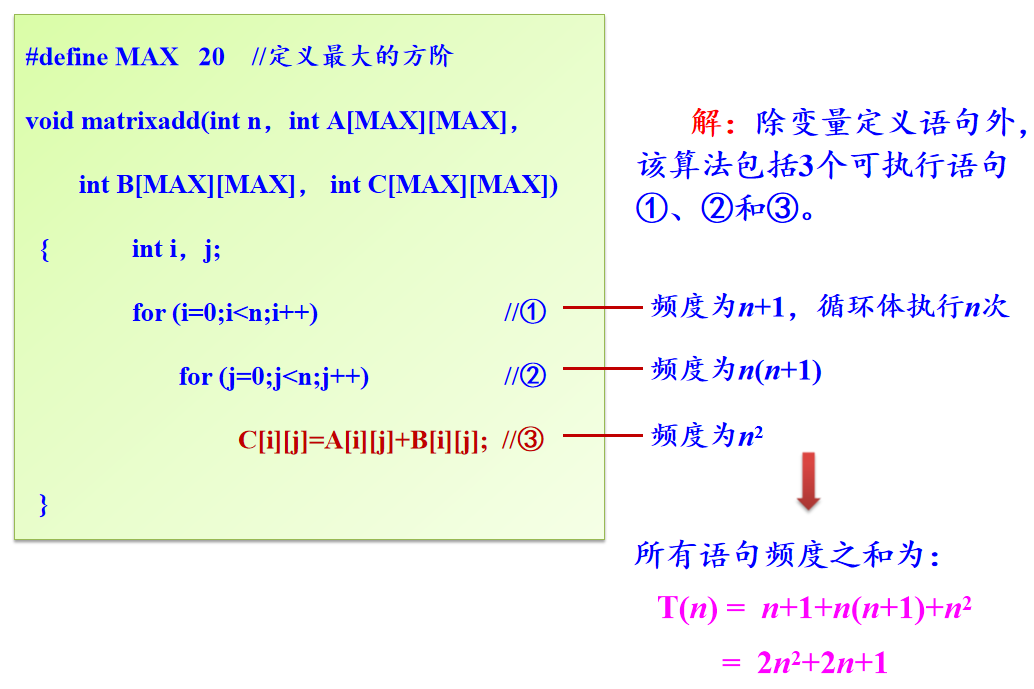
例:分析如下算法的时间复杂度
#define MAX 20
void matrixadd(int n,int A[MAX][MAX],int B[MAX][MAX],int C[MAX][MAX])
{
int i,j;
for (i=0;i<n;i++) //①
for (j=0;j<n;j++) //②
C[i][j]=A[i][j]+B[i][j]; //③
}
四、算法的执行时间用时间复杂度来表示
使用 O(n) 表示。
下面是一个结论,推导过程略:
只求出算法执行时间 T(n) 的最高阶,忽略其低阶项和常系数,这样既可简化 T(n) 的计算,又能比较客观地反映出当n很大时算法的时间性能。 ?
其他概念:
- 一个没有循环的算法的执行时间与问题规模n无关,记作 O(1),也称作常数阶。
- 一个只有一重循环的算法的执行时间与问题规模n的增长呈线性增大关系,记作 O(n),也称线性阶。
- 其余常用的算法时间复杂度还有平方阶 O(n^2)、立方阶 O(n^3)、对数阶 O(log^2n)、指数阶 O(2^n) 等。
各种不同算法时间复杂度的比较关系如下: ? ? ? ? ?
O(1) < O(log2n) < O(n) < O(nlog2n) < O(n2) < O(n3) < O(2n) < O(n!)
五、简化的算法时间复杂度分析
算法中的基本操作一般是最深层循环内的原操作。
即算法执行时间大致 = 基本操作所需的时间 × 其运算次数。?
也就是在进行简化的算法分析时,计算算法执行时间时仅仅考虑基本操作的运算次数。
例:


六、算法的空间复杂度
空间复杂度只与临时变量的个数有关。

上面例子定义了4个临时变量,与n无关,故为 O(1)。