目录
写在前面:
首先问大家一个问题:你真的完全理解二分查找了吗?
在接触到二分查找的细节之前我也这么认为,但其实二分查找难的并不是它的思想,而是它的细节处理。
如果你对二分查找的边界问题及两段性有很好的理解,那么这篇博客就对你来说是没有用的,但是对于没听说过它的边界问题以及两段性的人来说,这是一篇有价值的博客。
本次本文就二分查找的边界处理及其延伸的两段性为大家带来讲解。
?1. 什么是二分查找
如果你没有了解过二分查找,那么点这里:图解二分查找![]() https://blog.csdn.net/m0_63303316/article/details/122443029?spm=1001.2014.3001.5501
https://blog.csdn.net/m0_63303316/article/details/122443029?spm=1001.2014.3001.5501
?二分查找的功能有多强大?
下面为大家举个栗子:
要在有序的1~1000个数字中找一个数字,如果通过遍历的方式来找数字的话,最坏的结果需要找1000次,而通过二分查找,每次都范围都折半,最多只要找10次,时间复杂度由O(n)变为O(logn),在公司中,这也是经常被使用到的算法。
2. 左闭右闭 左闭右开和左开右闭
ps:这里将用一道例题的三种不同解法来像大家解释什么是左闭右闭 左闭右开和左开右闭
704. 二分查找 - 力扣(LeetCode) (leetcode-cn.com)![]() https://leetcode-cn.com/problems/binary-search/
https://leetcode-cn.com/problems/binary-search/

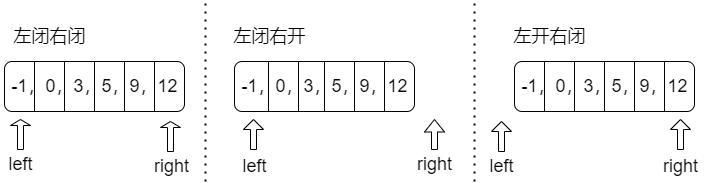
- 左闭右闭代表的就是[left,right]的区间,也就是left=0,right=?numsSize-1
- 左闭右开代表的就是[left,right)的区间,也就是left=0,right=?numsSize
- 左闭右闭代表的就是(left,right]的区间,也就是left=-1,right=?numsSize-1
?三种取值范围的写法区别在于:
(1)每次折半的时候两端的坐标应该移到mid的位置上还是多偏移一个元素
(2)while判断结束的条件是left<right还是left<=right
(3)对于mid的取值
?接下来将具体介绍它们之间的差别
3. 处理三种情况的代码:
ps:我将例举三种情况的代码实现方式,并参照第一种(左闭右闭)的代码标注出差别
3.1 左闭右闭代码实现
int search(int* nums, int numsSize, int target){
int left = 0;//差别1
int right = numsSize - 1;
int ans = -1;
while (left <= right)
{
int mid = left + (right - left) / 2;
if (target < nums[mid])
{
right = mid - 1;
}
else if (target > nums[mid])
{
left = mid + 1;
}
else
{
ans = mid;
break;
}
}
return ans;
}3.2 左闭右开代码实现
int search(int* nums, int numsSize, int target){
int left = 0;
int right = numsSize;//差别1
int ans = -1;
while (left < right)//差别2
{
int mid = left + (right - left) / 2;
if (target < nums[mid])
{
right = mid;//差别3
}
else if (target > nums[mid])
{
left = mid + 1;
}
else
{
ans = mid;
break;
}
}
return ans;
}3.3 左开右闭代码实现
int search(int* nums, int numsSize, int target){
int left = -1;//差别1
int right = numsSize;
int ans = -1;
while (left < right)//差别2
{
int mid = left + (right - left) / 2 + 1;//差别3
if (target < nums[mid])
{
right = mid - 1;
}
else if (target > nums[mid])
{
left = mid;//差别4
}
else
{
ans = mid;
break;
}
}
return ans;
}?4.区别详解
4.1 mid的偏移
当我们确定取值范围后,在缩小它的取值范围的过程中要保持一致,如下:
首先:假设我们查找的值为2
(1)若取值范围为左闭右闭,要找的值比mid小,那么right就应该移到mid-1的位置上;要找的值比mid小,那么left就应该移到mid+1的位置上
原因是:由于一开始确定的取值范围为[left,right],因此在后续查找缩小范围的时候,right也应该保持闭区间的形式,由于此时要找的值为2,mid的值为3,而mid的值由于已经被比较过了才得知mid比要找的值大,因此待搜索的范围缩小为[left,mid-1]。
(2)若取值范围为左闭右开,要找的值比mid小,那么right就应该移动到mid上;要找的值比mid小left就应该移动到mid+1上。

?原因是:由于有一开始确定的范围为[left,right),后续缩小范围的时候right也要保持开区间。由于mid的值已经被比较过,因此待搜索的范围缩小为[left,mid)。
?如果right=mid-1,也就意味着搜索的范围变为[left,mid-1)了,由于3就落在mid-1的坐标上,如果你要查找的数字为3,那么3是查找不到的。
(3)同(2)理:若取值范围为左开右闭,要找的值比mid小,那么right就应该移动到mid-1上;要找的值比mid小left就应该移动到mid上。
接下来我将就左闭右开的情况为大家举几个例子:
①假设一个数组为{0,1,2,3,4,5,6,7,8,9},需要索引的值为4
第一次我们的mid值为5,mid指向数字5,如果用right = mid-1处理,那么它的索引范围就变成[0,4)那么数字4就索引不到:

我们发现mid无法索引到存在的4,?因此在左闭右开的情况下用right=mid-1处理是不靠谱的,必须使用right=mid来处理。
同理:在左开右闭的情况写写成left=mid+1同样也是不靠谱的,必须用left=mid来处理
?-----------------------?--------------------------- ? ?
②假设一个数组为{0,1,2,3,4,5,6,7,8,9},
如果用left=mid处理,有可能找有些值就会死循环。
这里我们假设某种情况下left指向6,right指向7
第一次mid会指向6,如果用left=mid处理,则left还是指向6,从而进入死循环,因此在左闭右开的情况下用left=mid处理时不靠谱的。?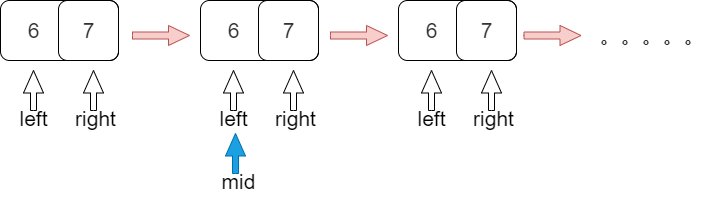
?同理:在左闭右闭的情况下必须用left=mid+1,right=mid-1处理;左开右闭的情况下必须用right=mid-1处理
4.2 循环条件的差别及原因
如果为左闭右闭那么while里面的判断语句是left<=right?;若为左闭右开或者左开右闭,则while的判断语句是left < right
假设一个数组为{0,1,2,3,4,5,6,7,8,9},
①左闭右闭 假设我们想要索引到6这个数字,缩小范围到某一时刻left和right都指向6,那么此时的索引区间为[left,right](也就是[6,6]),也就是说6这个数字还没有找过,因此当left=right时,还要继续找,使mid=(left+right)/2 = 6,再与索引值进行比较才能得到6这个值,所以while里的条件要写成(left <= right)。如果写成(left<right),那么当left和right都指向6的时候,循环结束,6这个数字就无法被索引到
假设一个数组为{0,1,2,3,4,5,7,8,9},
②左闭右开 假设当left和right都指向数字7,我们想要索引到数字6,那么索引区间为[left,right)(也就是[6,6))此时索引区间已经没有数字可以进行查找了,如果将条件写为(left<=right)那么它还会继续索引使mid=(left+right)/2还是指向数字7,索引值比mid指向的值要小,因此right=mid,则又陷入死循环,所以while里面的条件要写成(left < right)
③左开右闭
左开右闭和左闭右开的道理是一样的,left和right都指向一个数字的时候,mid也指向那个数字,不过和左闭右开的区别是:当它索引的值比mid大的时候,因此left=mid,才陷入死循环,所以while里面的条件要写成(left < right)
4.3 mid的取值方式及其原因
对比三段代码mid的取值方式,我们发现第三种的实现情况和前两种并不一样,这时为什么呢?
由于当两个边界中间的元素为偶数个时,不同的取法会导致mid值的偏向不同
1.当left和right之间的元素为偶数个时,下面两种情况会使mid偏向中间偏左的元素
(1)(left+right)/2
(2)left+(right - left)/2

例子:当左开右闭的时候,如果索引的元素在0~3之间,以2的索引为例子,如果mid为上面两种写法,那么当left指向第一个元素,而right指向第二个元素并且需索引的值比mid的值大(left=mid)的时候,left和mid会反复指向第一个元素,进入死循环:

???????-----------------------?--------------------------- ? ?
2.当left和right之间的元素为偶数个时,下面两种情况会使mid偏向中间偏右的元素
(3)(left+right+1)/2
(4)left+(right - left + 1)/2

?同理:当左闭右开的时候,如果索引的元素在5~9之间,以7的索引为例子,如果mid为上面两种写法,那么当right指向最后一个元素,而left指向倒数第二个元素并且需索引的值比mid的值小(right=mid)的时候,right和mid会反复指向最后第一个元素,进入死循环。
总结:左闭右闭的时候四种写法都可以,左闭右开的时候只能用(1) (2)种写法,左开右闭时只能用(3)(4)种写法
[mid取值的一个小tips]
问:既然(left+right)/2和left+(right-left)/2的效果是相同的,为什么推荐用第二种写法呢?
答:其实使为了防溢出,left+right存在溢出的问题,因此用left+(right-left)/2的写法更为标准
5. 总结?
5.1?三种写法:left和right最初的取值
①左闭右闭:left=0,right=numSize-1
②左闭右开:left=0,right=numSize
③左开右闭:left=-1,right=numSize-1
5.2?三种写法:left和right索引时的偏移
①左闭右闭:left = mid + 1, right = mid - 1
②左闭右开:left = mid + 1, right = mid
③左开右闭:left = mid, right = mid - 1
5.3?三种写法:while里的循环条件
①左闭右闭:left <= right
②左闭右开:left < right
③左开右闭:left < right
5.4?三种写法:mid的取值
①左闭右闭:mid = left + (right - left) / 2 或者?mid = left + (right - left + 1) / 2
②左闭右开:mid = left + (right - left) / 2
③左开右闭:mid = left + (right - left + 1) / 2
6.? 二分查找的两段性问题
旋转数组的最小值![]() https://www.nowcoder.com/questionTerminal/9f3231a991af4f55b95579b44b7a01ba
https://www.nowcoder.com/questionTerminal/9f3231a991af4f55b95579b44b7a01ba
?如示例1 数组[3,4,5,1,2]是由一个非降序数组[1,2,3,4,5]向右旋转三次得到的

?思路:目的是为了找到右半段区间的最左边的元素就是旋转数组的最小值,左旋或者右旋都会产生上图的两端单调区间。利用二分查找,使用中间值与左端进行比较。
①首先取mid = left + (right - left) / 2,用arr[mid]的元素,来与arr[0]进行比较,如果比arr[0]大,那么arr[mid]就位于左半段区间,如果比arr[0]小,那么arr[mid]就位于右半段区间
②如果mid位于左半段区间,那么left = mid+1,使它的left靠近右半段区间,直到left位于右半段,则转化成了再有序数组中索引一个值的二分查找问题
③如果mid位于右半段区间,那么right = mid,使范围缩小为[left, mid],这里为什么是right = mid呢?由于我们要找的是右半段区间的最左边的值,假设mid指向右半段区间的最左边值,那么用right=mid-1就会使它的区间变成[left, mid-1],那么就无法找到右半段最左边的值了

④最后,left指向的值就是它的最小值?

????-----------------------?--------------------------- ?
因此我们可以写出以下以下代码:
int minNumberInRotateArray(int* rotateArray, int rotateArrayLen) {
// write code here
int left = 0;
int right = rotateArrayLen - 1;
int mid;
while (left < right)
{
mid = left + (right - left) / 2;
if (rotateArray[mid] < rotateArray[left])
right = mid;
if (rotateArray[mid] > rotateArray[left])
left = mid + 1;
}
return rotateArray[left];
}?但这还不是完全正确的,题目中只说了是非降序数组,因此数组中还可能有重复的元素,如下面的数组[1,0,1,1,1,1]是由数组[0,1,1,1,1,1]旋转而来的,这种情况下,如果mid指向的值与left指向的值相同那么就通过right--,把最小值向右推,因此可以写出下面代码
int minNumberInRotateArray(int* rotateArray, int rotateArrayLen ) {
// write code here
int left = 0;
int right = rotateArrayLen - 1;
int mid = 0;
while (left < right)
{
mid = (left + right) / 2;
if (*(rotateArray + right) > *(rotateArray + mid))
{
right = mid;
}
else if (*(rotateArray + right) == *(rotateArray + mid))
{
right--;
}
else
{
left = mid + 1;
}
}
return rotateArray[left];
}
-----------------------?--------------------------- ? ??
第一个错误版本![]() https://leetcode-cn.com/problems/first-bad-version/?
https://leetcode-cn.com/problems/first-bad-version/?
?思路:本题的思路其实和上一题是一样的,同样是在两段区间里找右边那段区间的最左边的值所在的下标。
本题用isBadVersion函数判断是否为错误版本,如果是错误版本,这个函数便返回true(1),是正确版本就返回false(0)。
因此可以看成左半段全是0,右半段全是1的区间,并找到右半段区间的最左边的元素所在的位置
?这里直接为大家给出代码啦:
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);
int firstBadVersion(int n) {
int left = 1;
int right = n;
int mid = 0;
while (left < right)
{
mid = left + (right - left) / 2;
if (isBadVersion(mid))
{
right = mid;
}
else
{
left = mid + 1;
}
}
return left;
}