题目描述
给定一个二维矩阵 matrix,以下类型的多个请求:
计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) 。
实现 NumMatrix 类:
NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 的子矩阵的元素总和。
题目来源
解题思考
思路1:使用双重循环,暴力求解。固定行数和列数,进行求和。
思路2:使用前缀和求解。首先求矩阵的前缀和,其次求子矩阵和。以下两个图方便理解。
计算矩阵前缀和:
preSum(x,y)=preSum(x-1,y)+preSum(x,y-1)-preSum(x-1,y-1)+matrix[x][y]。
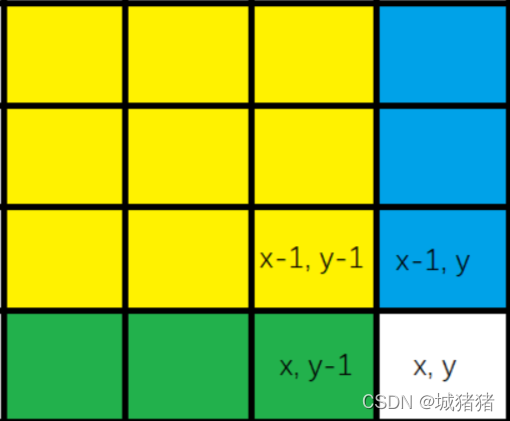
计算子矩阵的和:
Sum(x,y)=preSum(x2,y2)-preSum(x2,y1-1)-preSum(x1-1,y2)+preSum(x1-1,y1-1)。

代码实现
class NumMatrix(object):
def __init__(self, matrix):
"""
:type matrix: List[List[int]]
"""
self.preSum=[[0 for j in range(len(matrix[0])+1)] for i in range(len(matrix)+1)]
for i in range(len(matrix)):
for j in range(len(matrix[0])):
self.preSum[i+1][j+1]=self.preSum[i+1][j]+self.preSum[i][j+1]-self.preSum[i][j]+matrix[i][j]
def sumRegion(self, row1, col1, row2, col2):
"""
:type row1: int
:type col1: int
:type row2: int
:type col2: int
:rtype: int
"""
return self.preSum[row2+1][col2+1]-self.preSum[row2+1][col1]-self.preSum[row1][col2+1]+self.preSum[row1][col1]
# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)
性能评估
心得:
机会成本便是,当你做出某种选择时放弃的一些东西。