[数据结构与算法]优化工具包—无约束非线性优化求解器（fminsearch）

优化工具包—无约束非线性优化求解器（fminsearch）

原创不易，路过的各位大佬请点个赞

fminun优化函数见该链接

一、fminunc总体介绍

语法：

x = fminsearch(fun,x0)
x = fminsearch(fun,x0,options)
x = fminsearch(problem)
[x,fval] = fminsearch(___)
[x,fval,exitflag] = fminsearch(___)
[x,fval,exitflag,output] = fminsearch(___)

说明：
非线性规划求解器。搜索由以下公式指定的问题的最小值：
$$\underset{x}{\min }f(x)$$
$f(x)$是返回标量的函数，$x$是向量或矩阵；fminsearch求解器面向多变量函数；fminsearch适用于无约束非线性问题。如果需要优化的问题有约束，通常使用 fmincon。
相比fminunc（同样也是求无约束多变量函数的最小值），fminsearch使用无导数法计算最小值

x = fminsearch(fun,x0) 在点 x0 处开始并尝试求 fun 中描述的函数的局部最小值 x。

二、fminsearch求解器的具体用法

下面具体介绍fminunc求解器的用法

1）x = fminsearch(fun,x0) 在点 x0 处开始并尝试求 fun 中描述的函数的局部最小值 x;

2）x = fminsearch(fun,x0,options) 使用 options 所指定的优化选项执行最小化。使用 optimset 可设置这些选项。；

3）x = fminsearch(problem) 求 problem 的最小值，它是 problem 中所述的一个结构体；

4）[x,fval] = fminsearch(___)，对任何上述输入语法，在 fval 中返回目标函数 fun 在解 x 处的值。

5）[x,fval,exitflag] = fminsearch(___) 还返回描述退出条件的值 exitflag。

6）[x,fval,exitflag,output] = fminsearch(___) 还会返回结构体 output 以及有关优化过程的信息。

三、举例：计算 Rosenbrock 函数的最小值

计算 Rosenbrock 函数的最小值，对于许多算法来说，这是极难的优化问题：
Rosenbrock目标函数：
$$f(\mathbf{x})=100(x_2?x_1^2{)}^2+(1?x_1{)}^2$$
其中$x=[x_1,x_2]$为一个二维向量。
该函数的最小值在$\mathbf{x}=[1,1]$处，最小值为0；
下面我们将初始点设为$x_0=[?1.2,1]$，使用 fminsearch函数求解

代码：

fun = @(x)100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
x0 = [-1.2,1];
x = fminsearch(fun,x0)

求解结果：

x = 1×2

    1.0000    1.0000

四、设置选项：监视优化过程/检查优化过程

4.1 监视优化过程

设置选项，以监视 fminsearch 尝试定位最小值的过程。

设置选项，以在每次迭代时绘制目标函数图。

options = optimset(‘PlotFcns’,@optimplotfval);

将目标函数设置为 Rosenbrock 函数，
$$f(\mathbf{x})=100(x_2?x_1^2{)}^2+(1?x_1{)}^2$$
将起始点设置为$x_0=[?1.2,1]$ 并使用 fminsearch 计算 Rosenbrock 函数的最小值。

fun = @(x)100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
x0 = [-1.2,1];
x = fminsearch(fun,x0,options)

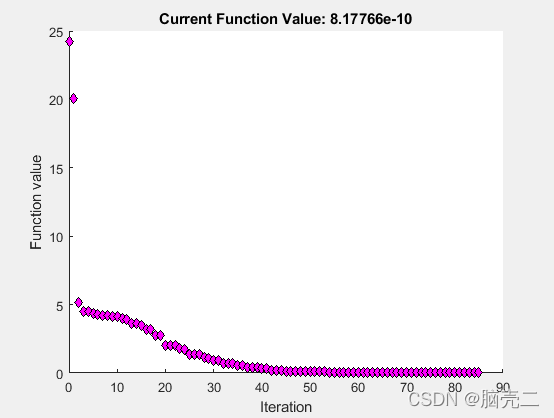
结果为：

x = 1×2

    1.0000    1.0000

4.2 检查优化过程
在优化进行期间和优化结束后检查优化结果。

将选项设置为提供迭代输出，从而在求解器运行时提供有关优化的信息。此外，将绘图函数设置为在求解器运行时显示目标函数值。

options = optimset(‘Display’,‘iter’,‘PlotFcns’,@optimplotfval);

设置目标函数和起始点。

function f = objectivefcn1(x)
f = 0;
for k = -10:10
    f = f + exp(-(x(1)-x(2))^2 - 2*x(1)^2)*cos(x(2))*sin(2*x(2));
end

将 objectivefcn1 的代码作为文件包含在您的 MATLAB? 路径中

x0 = [0.25,-0.25];
fun = @objectivefcn1;

获取所有求解器输出。在求解器运行完毕后，使用这些输出检查结果。

[x,fval,exitflag,output] = fminsearch(fun,x0,options)

具体结果显示不截图了

设置选项options 的细节见第六节

五、具有额外参数时求最小值

有时您的目标函数具有额外参数。这些参数不是要优化的变量，它们是优化过程中的固定值。例如，假设您在以下 Rosenbrock 类型函数中有一个参数 a：

$$f(\mathbf{x},a)=100(x_2?x_1^2{)}^2+(a?x_1{)}^2$$

此函数在$x_1=a$,$x_2=a^2$处具有最小值 0。

假如$a=3$，创建匿名函数将该参数包含在创建的目标函数中。

f = @(x,a)100*(x(2) - x(1)^2)^2 + (a-x(1))^2;

将参数放在您的 MATLAB? 工作区中，即

a=3

单独创建包含参数的工作区值的 x 的匿名函数。

fun = @(x)f(x,a);

在 $x0=[?1,1.9]$处开始解算该问题。

x0 = [-1,1.9];
x = fminsearch(fun,x0)

结果：

x = 1×2

    3.0000    9.0000

五、检查求解过程（options 设置）

优化选项，指定为 optimoptions 的输出或 optimset 等返回的结构体。

语法：

options = optimoptions(@fminunc,'Algorithm','quasi-newton');

其中’Algorithm’设置优化工具包用什么优化算法求解问题，其中fminunc函数可以用拟牛顿法和信赖域算法。
设置fminunc采用拟牛顿法求解：其中该函数’Algorithm’的默认值为’quasi-newton’

options = optimoptions(@fminunc,'Algorithm','quasi-newton');

quasi-newton 算法使用具有三次线搜索过程的 BFGS 拟牛顿法。这种拟牛顿法使用 BFGS公式来更新 Hessian 矩阵的逼近。您可以通过将 HessUpdate 选项设置为 ‘dfp’（并将 Algorithm 选项设置为 ‘quasi-newton’）来选择逼近逆 Hessian 矩阵的 DFP公式。您可以通过将 HessUpdate 设置为 ‘steepdesc’（并将 Algorithm 设置为 ‘quasi-newton’）来选择最陡下降法，尽管此设置通常效率不高。

设置fminunc采用信赖域算法求解：必须自己提供目标函数的梯度，不建议使用。

options = optimoptions(@fminunc,'Algorithm','trust-region');

trust-region 算法要求您在 fun 中提供梯度，并使用 optimoptions 将 SpecifyObjectiveGradient 设置为 true。此算法是一种子空间信赖域方法，基于 [2] 和 [3] 中所述的内部反射牛顿法。每次迭代都涉及使用预条件共轭梯度法 (PCG) 来近似求解大型线性方程组。

用法：

fun = @(x)x(1)*exp(-(x(1)^2 + x(2)^2)) + (x(1)^2 + x(2)^2)/20;
x0 = [1,2];
[x,fval,exitflag,output,grad,hessian] = fminunc(fun,x0，options)

其它options的参数表如下：

原创不易，路过的各位大佬请点个赞