[数据结构与算法]算法与数据结构（堆排序）

堆排序

1 什么是堆

要了解堆排序，首先要知道什么是堆。堆是一种逻辑结构，需要满足以下两个性质：

1. 堆是一颗完全二叉树。
2. 堆的孩子结点和父结点必须满足一定的关系。对于最大堆来说，任何父结点一定要大于其左右孩子结点，最小堆反之。

堆的存储结构可以用二叉树或数组来实现，在堆排序算法中使用数组来实现。

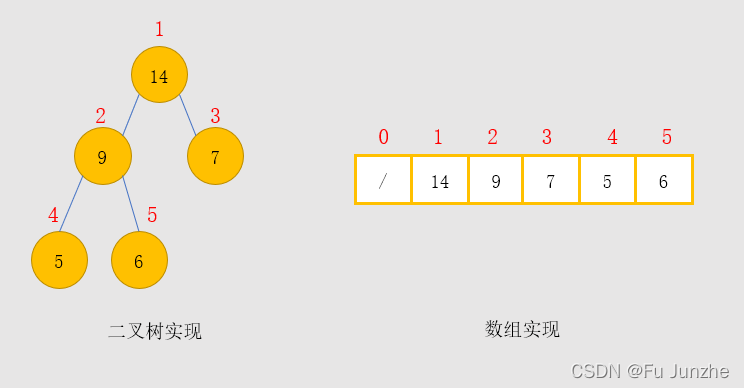
对于二叉树中序号值为 $i$ 的结点，如果其父结点和左右孩子结点存在，则其序号满足关系：

• 父结点序号 = $?i/2?$
• 左子结点序号 = $2i$
• 右子结点序号 = $2i+1$

为了使数组实现的堆也具有上述性质，一般将数组的第一位元素空出来。

2 最大堆的性质

对于最大堆来说，父结点一定大于其左右孩子结点，这就保证了每一层一定大于其下一层（层内不要求有序），最顶层的根结点一定是最大值。

那么如何构造最大堆呢？首先我们需要一个方法来维护最大堆的性质——父结点大于其左右子结点。原理很简单，比较父结点和左右子结点的大小，找出最大的那个值和父结点交换。但是交换后可能导致以该父结点为根的子数的堆结构被破坏（试想一下如果很不巧根结点是最小值，那么它会一直破坏子树的堆结构直到它变成叶结点为止），所以我们还需对改变后的子树进行维护。

void maxHeapify(vector<int>& heap, int len, int i) {
    int left = 2*i;
    int right = 2*i+1;
    int largest = i;
    // if left child exists
    if (left<=len && heap[left]>heap[i]) {
        largest = left;
    }
    // if right child exists
    if (right<=len && heap[right]>heap[largest]) {
        largest = right;
    }
    if (largest != i) {
        // exchange
        swap(heap[i], heap[largest]);
        // check if swap breaks the structure of next layer
        maxHeapify(heap, len, largest);
    }
}

有了这个方法，我们就可以对整颗树（逻辑上依然用树来描述，实际实现是用数组）自底向上地排序，构建一个最大堆。由于叶结点都没有孩子，因此以叶结点为根的二叉树已经满足堆的性质了。所以我们从后往前找第一个非叶结点，对它进行维护。然后自底向上的维护直到根结点。

void buildMaxHeap(vector<int>& heap) {
    int len = heap.size()-1;
    for (int i=len/2;i>0;i--) {
        maxHeapify(heap, len, i);
    }
}

之所是自底向上而非自顶向下，是因为维护方法有向下更新的特点，它始终会维持最底部满足堆的性质，而在交换的过程中很可能破坏上层的堆结构，如下例所示：

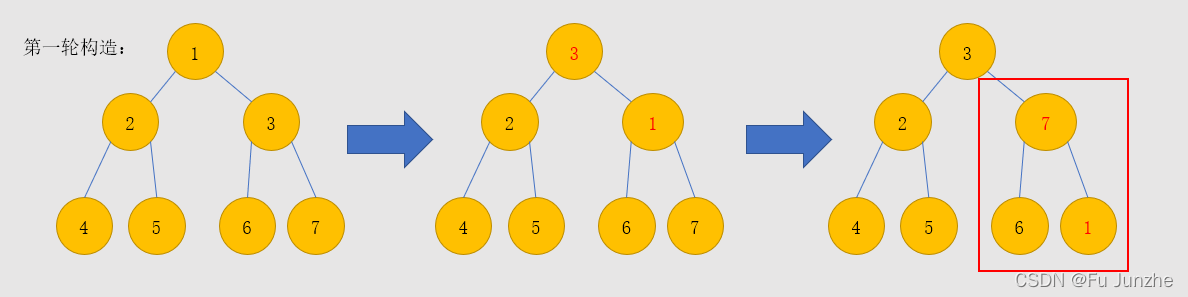
在第一轮构造中，我们从根结点开始，最终会使以 7 为根的子树维持堆的性质，但会破坏上层的堆结构。而在第二、第三轮构造中，我们都不会再调整根结点，因此最终会构造失败。

3 堆排序的实现

首先我们需要使用之前写好的堆构造函数 buildMaxHeap 来构造一个最大堆，此时堆顶就是最大值。我们可以将它与数组的最后一位元素交换，此时最大值就位于数组的最后一位，同时我们将该结点从堆中删除。剩余的结点中，原来的根的孩子结点仍然是最大堆，但是新的根结点可能会破坏堆结构，因此我们需要对根结点调用维护方法。

void heapsort(vector<int>& heap) {
    int len = heap.size()-1;
    // build heap
    buildMaxHeap(heap);
    for (int i=len;i>=2;i--) {
        // exchange
        swap(heap[i], heap[1]);
        // remove last element
        len--;
        maxHeapify(heap, len, 1);
    }
}

注意：这里只需要对根结点进行维护即可，不需要再从第一个非叶结点遍历。原因是除根结点外，此时其他结点都已处于最大堆的状态，当新的根结点向下移动时，它只有可能破坏它所在的那一路分支，其他分支依然处于有序状态。

代码实现

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 最大堆的维护方法
void maxHeapify(vector<int>& heap, int len, int i) {
    int left = 2*i;
    int right = 2*i+1;
    int largest = i;
    // if left child exists
    if (left<=len && heap[left]>heap[i]) {
        largest = left;
    }
    // if right child exists
    if (right<=len && heap[right]>heap[largest]) {
        largest = right;
    }
    if (largest != i) {
        // exchange
        swap(heap[i], heap[largest]);
        // check if swap breaks the structure of next layer
        maxHeapify(heap, len, largest);
    }
}

// 最大堆的构造方法
void buildMaxHeap(vector<int>& heap) {
    int len = heap.size()-1;
    for (int i=len/2;i>0;i--) {
        maxHeapify(heap, len, i);
    }
}

// 堆排序
void heapsort(vector<int>& heap) {
    int len = heap.size()-1;
    // build heap
    buildMaxHeap(heap);
    for (int i=len;i>=2;i--) {
        // exchange
        swap(heap[i], heap[1]);
        // remove last element
        len--;
        maxHeapify(heap, len, 1);
    }
}

// test
int main(int argc, char const *argv[])
{
    vector<int> heap = {0,1,2,3,4,5,6,7};
    // maxHeapify(heap, heap.size()-1, 1);
    buildMaxHeap(heap);
    // heapsort(heap);
    for (auto num : heap) {
        cout << num << endl;
    }
    return 0;
}